小学数学北京版六年级下册圆柱与圆锥课后作业题

六年级下册数学试题--圆柱与圆锥-116-人教新课标

一、判断题（共2题；共4分）

1.圆锥的高一定，它的体积与底面周长成正比例。（   ）   

【答案】 错误  

【考点】圆锥的体积（容积）   

【解析】【解答】解：圆锥的体积和圆锥的底面周长没有比例关系。
故答案为：错误。
【分析】圆锥的高一定，它的体积与底面积成正比例。

2.一个圆柱体和一个圆锥体的底面积之比为2：3，高的比为7：4，那么它们的体积之比为7：2。（   ）   

【答案】 正确  

【考点】圆柱的体积（容积），圆锥的体积（容积），比的应用   

【解析】【解答】解：（2×7）：（×3×4）=7：2，所以它们的体积之比是7：2。
故答案为：正确。
【分析】圆柱的体积=底面积×高，圆锥的体积=×底面积×高，然后作比即可。

二、填空题（共1题；共4分）

3.一个棱长为6分米的正方体木块，它的占地面积是________平方分米，它的表面积是________平方分米，体积是________立方分米，如果把它削成一个最大的圆锥体的体积是________立方分米．   

【答案】 36；216；216；56.52  

【考点】圆锥的体积（容积）   

【解析】【解答】解：占地面积：6×6=36（平方分米）；表面积：36×6=216（平方分米）；体积：36×6=216（立方分米）；
削成最大圆锥的体积：
3.14×（6÷2）2×6×
=3.14×18
=56.52（立方分米）
故答案为：36；216；216；56.52。

【分析】正方体占地面积就是底面积，用一个面的面积乘6就是正方体表面积，用底面积乘高就是正方体体积。正方体削成的最大圆锥的底面直径和高都是6分米，然后根据圆锥的体积公式计算即可。

三、解答题（共6题；共35分）

4.计算下面立体图形的表面积 

【答案】 解：3.14×（40÷2）²×2+3.14×40×60

=3.14×800+3.14×2400

=3.14×3200

=10048

【考点】圆柱的侧面积、表面积   

【解析】【分析】已知圆柱的底面直径和高，要求圆柱的表面积，用公式：圆柱的表面积=圆柱的侧面积+底面积×2，据此列式解答。

5.一种儿童玩具——陀螺（如图），上面是圆柱，下面是圆锥。经过测试，只有当圆柱底面直径为4厘米，高为5厘米，圆锥的高与圆柱的高的比是3：5时，才能旋转得又稳又快，试问这个陀螺的体积是多大？（保留整立方厘米） 

【答案】 解：3.14×（4÷2）2×5+ ×3.14×（4÷2）2×（5× ）=75.36≈75（立方厘米） 

答：这个陀螺的体积是75立方厘米。

【考点】圆柱的体积（容积），圆锥的体积（容积），组合体的体积的巧算   

【解析】【分析】根据题意可知，这个陀螺的体积=上面圆柱部分的体积+下面圆锥部分的体积，据此列式解答。

6.求圆锥的体积。 

【答案】 V=πr2h
=×3.14×42×15
=×3.14×16×15
=50.24×5
=251.2（cm3）  

【考点】圆锥的体积（容积）   

【解析】【分析】已知圆锥的底面半径r和高h，要求圆锥的体积V，用公式：V=πr2h，据此列式解答。

7.一个圆柱形的水桶，底面直径是40厘米，里面装有80厘米深的水。现将一个底面周长为62.8厘米的圆锥形铁块沉浸在水桶之中（水未溢出），水面升高了 ，圆锥形铁块的高是多少厘米？   

【答案】 解：解：3.14×（ ）2×80× ÷ ÷[3.14×（62.8÷3.14÷2）2]=60（厘米）

答：圆锥形铁块的高是60厘米。

【考点】圆锥的体积（容积）   

【解析】【分析】圆柱形水桶的底面积=（底面直径÷2）2×π，圆锥形铁块的底面积=（底面直径÷2）2×π，那么圆锥形铁块的高=圆柱形水桶的×水面升高的高度÷÷圆锥的底面积，据此代入数据作答即可。

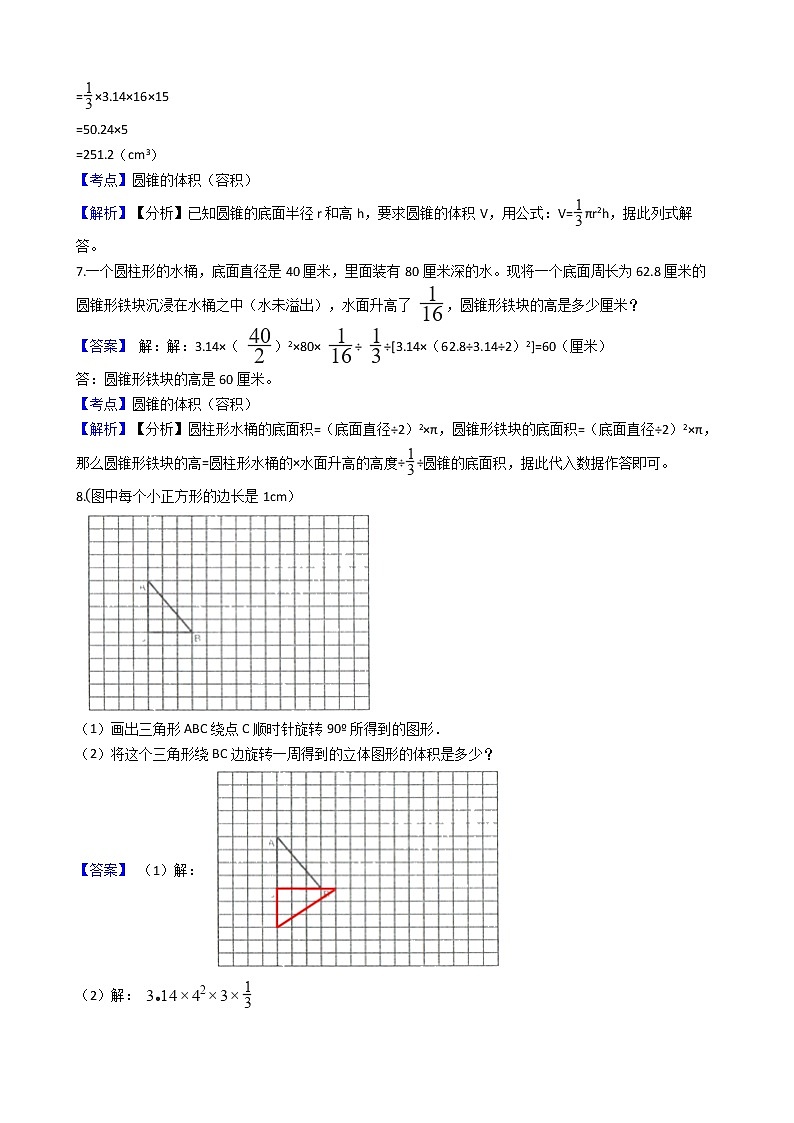
8.图中每个小正方形的边长是1cm） 

（1）画出三角形ABC绕点C顺时针旋转90º所得到的图形．   

（2）将这个三角形绕BC边旋转一周得到的立体图形的体积是多少？   

【答案】 （1）解： 
（2）解：

答：将这个三角形绕BC边旋转一周得到的立体图形的体积是50.24cm3。

【考点】圆锥的体积（容积），作旋转后的图形   

【解析】【分析】（1）先确定旋转中心，然后根据旋转方向和度数确定对应点的位置，再画出旋转后的图形即可；
（2）绕BC边旋转一周得到的图形是圆锥，底面半径是AC边，高是BC边，底面半径是4cm，高是3cm，根据圆锥的体积公式计算体积即可。

9.横截面直径为4cm的一段圆柱体木材，被截成三段后，三段的表面积的和是11304cm2  ， 求原来圆柱木材的体积是多少？
   

【答案】 解：圆柱的侧面积：
11304-3.14×（4÷2）2×6
=11304-75.36
=11228.64（平方厘米）
圆柱的高：11228.64÷（3.14×4）=894（厘米）
圆柱的体积：3.14×（4÷2）2×894
=3.14×4×894
=11228.64（立方厘米）
答：原来圆柱木材的体积是11228.64立方厘米。
  

【考点】圆柱的侧面积、表面积，圆柱的体积（容积），立方体的切拼   

【解析】【分析】把这个圆柱形木材截成三段后，共有6个圆形底面，因此用三段的表面积的和减去6个底面的面积即可求出侧面积之和，也就是原来圆柱的侧面积。用侧面积除以底面周长即可求出原来圆柱的高，然后用底面积乘高即可求出原来圆柱的体积。

试卷分析部分

1. 试卷总体分布分析

2. 试卷题量分布分析

3. 试卷难度结构分析

4. 试卷知识点分析