2022年河北省正定县重点中学中考联考数学试题含解析

2021-2022中考数学模拟试卷

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）

1．如图，Rt△ABC中，∠C=90°，AC=4，BC=4，两等圆⊙A，⊙B外切，那么图中两个扇形（即阴影部分）的面积之和为（　　）

A．2π B．4π C．6π D．8π

2．如图，在平面直角坐标系xOy中，点A从出发，绕点O顺时针旋转一周，则点A不经过（    ）

A．点M B．点N C．点P D．点Q

3．如图，等边三角形ABC的边长为3，N为AC的三等分点，三角形边上的动点M从

点A出发，沿A→B→C的方向运动，到达点C时停止．设点M运动的路程为x，MN2=y，则y关于x的函数图象大致为

A．       B．       C．       D．

4．如果一组数据6，7，x，9，5的平均数是2x，那么这组数据的中位数为（    ）

A．5 B．6 C．7 D．9

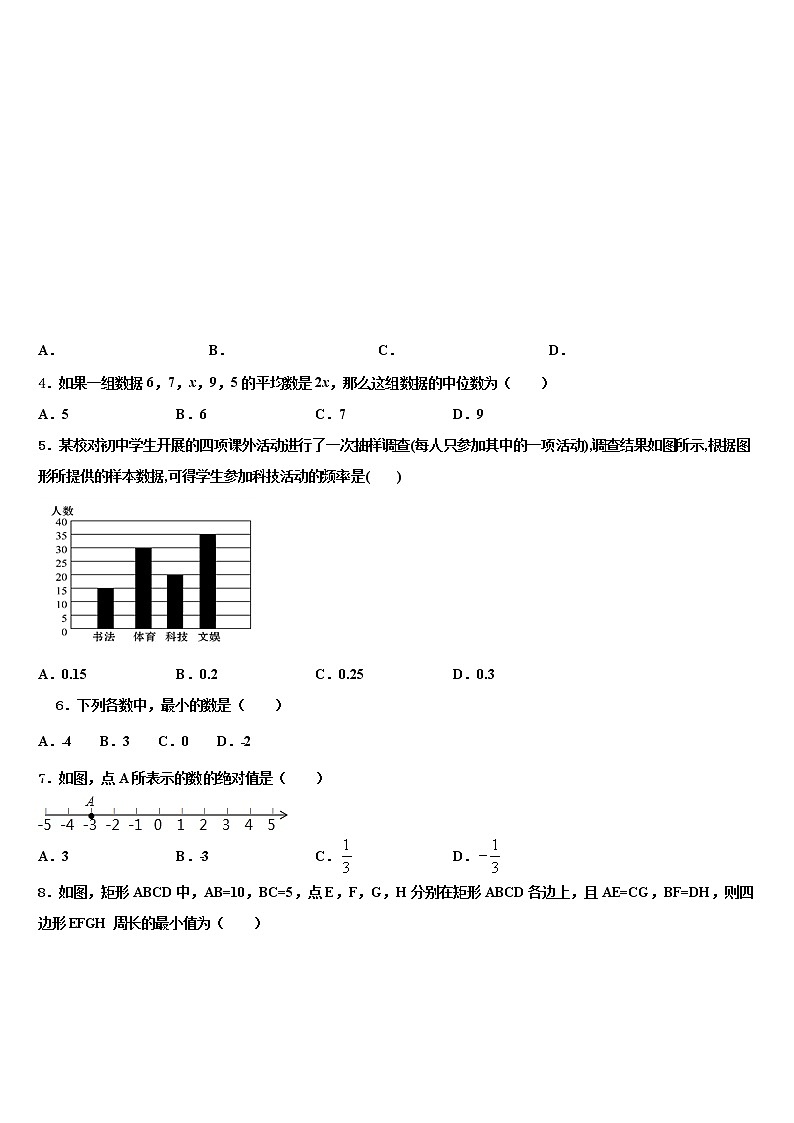
5．某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示,根据图形所提供的样本数据,可得学生参加科技活动的频率是(　　)

A．0.15 B．0.2 C．0.25 D．0.3

6．下列各数中，最小的数是（    ）

A．﹣4    B．3    C．0    D．﹣2

7．如图，点A所表示的数的绝对值是（　　）

A．3 B．﹣3 C． D．

8．如图，矩形ABCD中，AB=10，BC=5，点E，F，G，H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为（　　）

A．5 B．10 C．10 D．15

9．在实数π，0，，﹣4中，最大的是（　　）

A．π B．0 C． D．﹣4

10．已知点P（a，m），Q（b，n）都在反比例函数y=的图象上，且a＜0＜b，则下列结论一定正确的是（　　）

A．m+n＜0 B．m+n＞0 C．m＜n D．m＞n

二、填空题（共7小题，每小题3分，满分21分）

11．若圆锥的地面半径为，侧面积为，则圆锥的母线是__________．

12．计算： 7＋(－5)＝______．

13．一个不透明的口袋中有5个红球，2个白球和1个黑球，它们除颜色外完全相同，从中任意摸出一个球，则摸出的是红球的概率是_____．

14．如图，正方形ABCD的边长为，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB， 垂足为点F，则EF的长是__________．  

15．我国自主研发的某型号手机处理器采用10 nm工艺，已知1 nm=0.000000001 m，则10 nm用科学记数法可表示为_____m．

16．一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球．每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球_____个．

17．关于x的分式方程=2的解为正实数，则实数a的取值范围为_____．

三、解答题（共7小题，满分69分）

18．（10分）如图，在平面直角坐标系中，等边三角形ABC的顶点B与原点O重合，点C在x轴上，点C坐标为（6，0），等边三角形ABC的三边上有三个动点D、E、F（不考虑与A、B、C重合），点D从A向B运动，点E从B向C运动，点F从C向A运动，三点同时运动，到终点结束，且速度均为1cm/s，设运动的时间为ts，解答下列问题：

（1）求证：如图①，不论t如何变化，△DEF始终为等边三角形．

（2）如图②过点E作EQ∥AB，交AC于点Q，设△AEQ的面积为S，求S与t的函数关系式及t为何值时△AEQ的面积最大？求出这个最大值．

（3）在（2）的条件下，当△AEQ的面积最大时，平面内是否存在一点P，使A、D、Q、P构成的四边形是菱形，若存在请直接写出P坐标，若不存在请说明理由？

19．（5分）解方程：2(x-3)=3x(x-3)．

20．（8分）经过校园某路口的行人，可能左转，也可能直行或右转．假设这三种可能性相同，现有小明和小亮两人经过该路口，请用列表法或画树状图法，求两人之中至少有一人直行的概率．

21．（10分）如图，在平行四边形中，的平分线与边相交于点．

（1）求证；

（2）若点与点重合，请直接写出四边形是哪种特殊的平行四边形．

22．（10分）已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB 的平分线．

求证：AB=DC．

23．（12分）某地铁站口的垂直截图如图所示，已知∠A=30°，∠ABC=75°，AB=BC=4米，求C点到地面AD的距离（结果保留根号）．

24．（14分）先化简，再选择一个你喜欢的数（要合适哦！）代入求值：.

参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）

1、B

【解析】
先依据勾股定理求得AB的长，从而可求得两圆的半径为4，然后由∠A+∠B=90°可知阴影部分的面积等于一个圆的面积的．

【详解】

在△ABC中，依据勾股定理可知AB==8，

∵两等圆⊙A，⊙B外切，

∴两圆的半径均为4，

∵∠A+∠B=90°，

∴阴影部分的面积==4π．

故选：B．

【点睛】

本题主要考查的是相切两圆的性质、勾股定理的应用、扇形面积的计算，求得两个扇形的半径和圆心角之和是解题的关键．

2、C

【解析】
根据旋转的性质：对应点到旋转中心的距离相等，逐一判断即可.

【详解】

解：连接OA、OM、ON、OP，根据旋转的性质，点A的对应点到旋转中心的距离与OA的长度应相等

根据网格线和勾股定理可得：OA=，OM=，ON=，OP=，OQ=5

∵OA=OM=ON=OQ≠OP

∴则点A不经过点P

故选C.

【点睛】

此题考查的是旋转的性质和勾股定理，掌握旋转的性质：对应点到旋转中心的距离相等和用勾股定理求线段的长是解决此题的关键.

3、B

【解析】

分析：分析y随x的变化而变化的趋势，应用排它法求解，而不一定要通过求解析式来解决：

∵等边三角形ABC的边长为3，N为AC的三等分点，

∴AN=1。∴当点M位于点A处时，x=0，y=1。

①当动点M从A点出发到AM=的过程中，y随x的增大而减小，故排除D；

②当动点M到达C点时，x=6，y=3﹣1=2，即此时y的值与点M在点A处时的值不相等，故排除A、C。

故选B。

4、B

【解析】
直接利用平均数的求法进而得出x的值，再利用中位数的定义求出答案．

【详解】

∵一组数据1，7，x，9，5的平均数是2x，

∴，

解得：，

则从大到小排列为：3，5，1，7，9，

故这组数据的中位数为：1．

故选B．

【点睛】

此题主要考查了中位数以及平均数，正确得出x的值是解题关键．

5、B

【解析】

读图可知：参加课外活动的人数共有(15+30+20+35)=100人，

其中参加科技活动的有20人，所以参加科技活动的频率是=0.2，

故选B.

6、A

【解析】
有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可

【详解】

根据有理数比较大小的方法，可得

﹣4＜﹣2＜0＜3

∴各数中，最小的数是﹣4

故选：A

【点睛】

本题考查了有理数大小比较的方法，解题的关键要明确：①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小

7、A

【解析】
根据负数的绝对值是其相反数解答即可．

【详解】

|-3|=3，

故选A．

【点睛】

此题考查绝对值问题，关键是根据负数的绝对值是其相反数解答．

8、B

【解析】

作点E关于BC的对称点E′，连接E′G交BC于点F，此时四边形EFGH周长取最小值，过点G作GG′⊥AB于点G′，如图所示，

∵AE=CG，BE=BE′，

∴E′G′=AB=10，

∵GG′=AD=5，

∴E′G=，

∴C四边形EFGH=2E′G=10，

故选B．

【点睛】本题考查了轴对称-最短路径问题，矩形的性质等，根据题意正确添加辅助线是解题的关键．

9、C

【解析】
根据实数的大小比较即可得到答案.

【详解】

解：∵16＜17＜25，∴4＜＜5，∴＞π＞0＞－4，故最大的是，故答案选C.

【点睛】

本题主要考查了实数的大小比较，解本题的要点在于统一根据二次根式的性质，把根号外的移到根号内，只需比较被开方数的大小.

10、D

【解析】
根据反比例函数的性质，可得答案．

【详解】

∵y=−的k=-2＜1，图象位于二四象限，a＜1，

∴P（a，m）在第二象限，

∴m＞1；

∵b＞1，

∴Q（b，n）在第四象限，

∴n＜1．

∴n＜1＜m，

即m＞n，

故D正确；

故选D．

【点睛】

本题考查了反比例函数的性质，利用反比例函数的性质：k＜1时，图象位于二四象限是解题关键．

二、填空题（共7小题，每小题3分，满分21分）

11、13

【解析】

试题解析：圆锥的侧面积=×底面半径×母线长，把相应数值代入即可求解．

设母线长为R，则： 

解得:

故答案为13.

12、2

【解析】
根据有理数的加法法则计算即可.

【详解】

.

故答案为：2.

【点睛】

本题考查有理数的加法计算，熟练掌握加法法则是关键.

13、

【解析】
根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．

【详解】

解：由于共有8个球，其中红球有5个，则从袋子中随机摸出一个球，摸出红球的概率是．

故答案为．

【点睛】

本题考查了概率的求法，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．

14、2

【解析】
设EF=x，先由勾股定理求出BD，再求出AE=ED，得出方程，解方程即可．

【详解】

设EF=x，
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，∠ABD=∠ADB=45°，
∴BD=AB=4+4，EF=BF=x，
∴BE=x，
∵∠BAE=22.5°，
∴∠DAE=90°-22.5°=67.5°，
∴∠AED=180°-45°-67.5°=67.5°，
∴∠AED=∠DAE，
∴AD=ED，
∴BD=BE+ED=x+4+2=4+4，
解得：x=2，
即EF=2.

15、1×10﹣1

【解析】
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

【详解】

解：10nm用科学记数法可表示为1×10-1m，
故答案为1×10-1．

【点睛】

本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．

16、8

【解析】

试题分析：设红球有x个，根据概率公式可得，解得：x＝8.

考点：概率.

17、a＜2且a≠1

【解析】
将a看做已知数，表示出分式方程的解，根据解为非负数列出关于a的不等式，求出不等式的解集即可得到a的范围．

【详解】

分式方程去分母得：x+a-2a=2(x-1)，

解得：x=2-a，

∵分式方程的解为正实数，

∴2-a>0,且2-a≠1，

解得：a＜2且a≠1．

故答案为：a＜2且a≠1．

【点睛】

分式方程的解．

三、解答题（共7小题，满分69分）

18、（1）证明见解析；（2）当t=3时，△AEQ的面积最大为cm2；（3）（3，0）或（6，3）或（0，3）

【解析】
（1）由三角形ABC为等边三角形，以及AD=BE=CF，进而得出三角形ADF与三角形CFE与三角形BED全等，利用全等三角形对应边相等得到BF=DF=DE，即可得证；（2）先表示出三角形AEC面积，根据EQ与AB平行，得到三角形CEQ与三角形ABC相似，利用相似三角形面积比等于相似比的平方表示出三角形CEQ面积，进而表示出AEQ面积，利用二次函数的性质求出面积最大值，并求出此时Q的坐标即可；（3）当△AEQ的面积最大时，D、E、F都是中点，分两种情形讨论即 可解决问题；

【详解】

（1）如图①中，

∵C（6，0），

∴BC=6

在等边三角形ABC中，AB=BC=AC=6，∠A=∠B=∠C=60°，

由题意知，当0＜t＜6时，AD=BE=CF=t，

∴BD=CE=AF=6﹣t，

∴△ADF≌△CFE≌△BED（SAS），

∴EF=DF=DE，

∴△DEF是等边三角形，

∴不论t如何变化，△DEF始终为等边三角形；

（2）如图②中，作AH⊥BC于H，则AH=AB•sin60°=3，

∴S△AEC=×3×（6﹣t）=，

∵EQ∥AB，

∴△CEQ∽△ABC，

∴=（）2=，即S△CEQ=S△ABC=×9=，

∴S△AEQ=S△AEC﹣S△CEQ=﹣=﹣（t﹣3）2+，

∵a=﹣＜0，

∴抛物线开口向下，有最大值，

∴当t=3时，△AEQ的面积最大为cm2，

（3）如图③中，由（2）知，E点为BC的中点，线段EQ为△ABC的中位线，

当AD为菱形的边时，可得P1（3，0），P3（6，3），

当AD为对角线时，P2（0，3），

综上所述，满足条件的点P坐标为（3，0）或（6，3）或（0，3）．

【点睛】

本题考查四边形综合题、等边三角形的性质和判定、菱形的判定和性质、二次函数的性质等知识，解题的关键是学会构建二次函数解决最值问题，学会用分类讨论的思想思考问题，属于中考压轴题．

19、.

【解析】
先进行移项，在利用因式分解法即可求出答案.

【详解】

，

移项得：，

整理得：，

或，

解得：或．

【点睛】

本题考查了解一元一次方程-因式分解，熟练掌握因式分解的技巧是本题解题的关键.

20、两人之中至少有一人直行的概率为．

【解析】

【分析】画树状图展示所有9种等可能的结果数，找出“至少有一人直行”的结果数，然后根据概率公式求解．

【详解】画树状图为：

共有9种等可能的结果数，其中两人之中至少有一人直行的结果数为5，

所以两人之中至少有一人直行的概率为．

【点睛】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．概率=所求情况数与总情况数之比．

21、（1）见解析；(2)菱形.

【解析】
（1）根据角平分线的性质可得∠ADE=∠CDE，再由平行线的性质可得AB∥CD,易得AD=AE，从而可证得结论；

（2）若点与点重合，可证得AD=AB，根据邻边相等的平行四边形是菱形即可作出判断.

【详解】

（1）∵DE平分∠ADC，

∴∠ADE=∠CDE.

∵四边形ABCD是平行四边形，

∴AB∥CD,AB=CD,AD=BC,AB=CD.

∵∠AED=∠CDE.

∴∠ADE=∠AED.

∴AD=AE.

∴BC=AE.

∵AB=AE+EB.

∴BE+BC=CD.

(2)菱形，理由如下：

由（1）可知，AD=AE,

∵点E与B重合，

∴AD=AB.

∵四边形ABCD是平行四边形

∴平行四边形ABCD为菱形.

【点睛】

本题考查了平行四边形的性质，平行线的性质，等腰三角形的性质，菱形的性质，熟练掌握各知识是解题的关键.

22、∵平分平分，

∴

在与中，

．

【解析】

分析：根据角平分线性质和已知求出∠ACB=∠DBC，根据ASA推出△ABC≌△DCB，根据全等三角形的性质推出即可．

解答：证明：∵AC平分∠BCD，BC平分∠ABC，

∴∠DBC=∠ABC，∠ACB=∠DCB，

∵∠ABC=∠DCB，

∴∠ACB=∠DBC，

∵在△ABC与△DCB中，

，

∴△ABC≌△DCB，

∴AB=DC．

23、C点到地面AD的距离为：（2+2）m．

【解析】
直接构造直角三角形，再利用锐角三角函数关系得出BE，CF的长，进而得出答案．

【详解】

过点B作BE⊥AD于E，作BF∥AD，过C作CF⊥BF于F，

在Rt△ABE中，∵∠A=30°，AB=4m，

∴BE=2m，

由题意可得：BF∥AD，

则∠FBA=∠A=30°，

在Rt△CBF中，

∵∠ABC=75°，

∴∠CBF=45°，

∵BC=4m，

∴CF=sin45°•BC=

∴C点到地面AD的距离为：

【点睛】

考查解直角三角形，熟练掌握锐角三角函数是解题的关键.

24、1

【解析】解：

取时，原式．