2021-2022学年四川省遂宁市大英县中考数学全真模拟试卷含解析

这是一份2021-2022学年四川省遂宁市大英县中考数学全真模拟试卷含解析，共22页。

2021-2022中考数学模拟试卷
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（　　）

A．84 B．336 C．510 D．1326
2．下列计算正确的是（　　）
A． +＝ B．﹣＝ C．×＝6 D．＝4
3．如图，为了测量河对岸l1上两棵古树A、B之间的距离，某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点，测得∠ACB＝15°，∠ACD＝45°，若l1、l2之间的距离为50m，则A、B之间的距离为（　　）

A．50m B．25m C．（50﹣）m D．（50﹣25）m
4．在实数0，－π，，－4中，最小的数是（ ）
A．0 B．－π C． D．－4
5．如图，已知E，B，F，C四点在一条直线上，，，添加以下条件之一，仍不能证明≌的是　　

A． B． C． D．
6．在Rt△ABC中，∠C=90°，BC=a，AC=b，AB=c，下列各式中正确的是（　　）
A．a=b•cosA B．c=a•sinA C．a•cotA=b D．a•tanA=b
7．如图，两个一次函数图象的交点坐标为，则关于x，y的方程组的解为（ ）

A． B． C． D．
8．如图，等腰△ABC的底边BC与底边上的高AD相等，高AD在数轴上，其中点A，D分别对应数轴上的实数﹣2，2，则AC的长度为（　　）

A．2 B．4 C．2 D．4
9．下列图形中，是中心对称图形但不是轴对称图形的是（　　）
A． B． C． D．
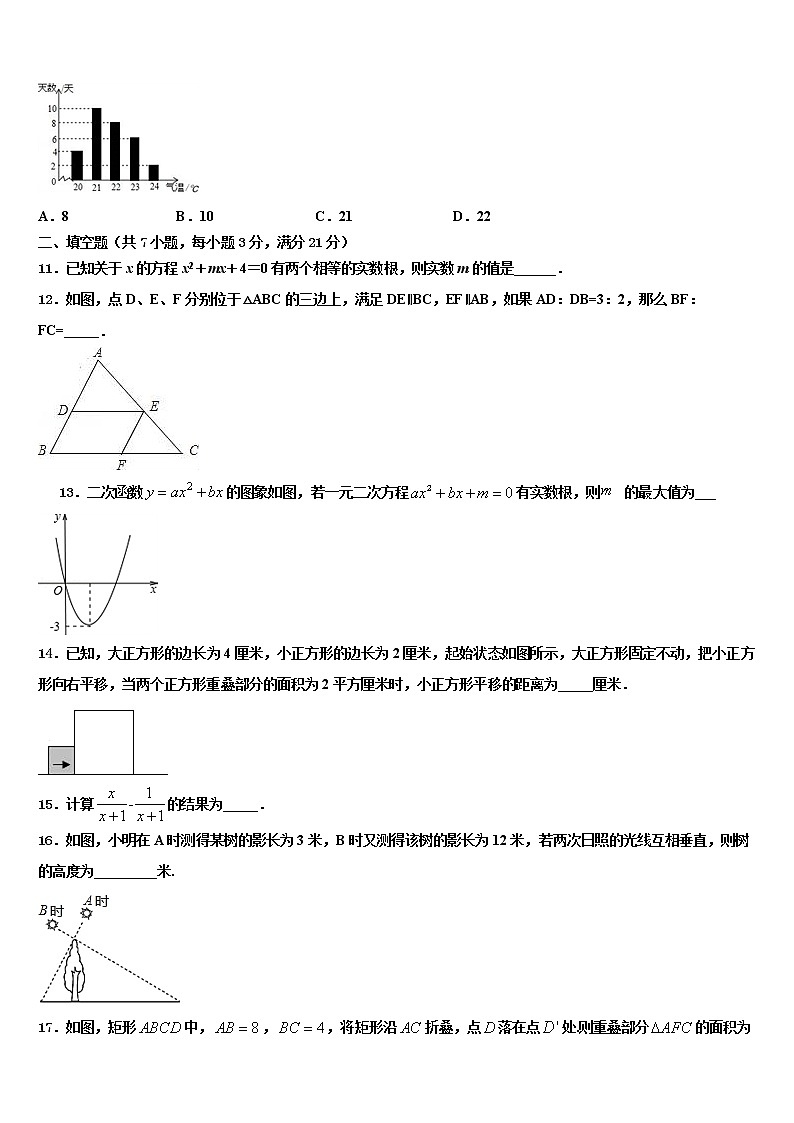
10．某市6月份日平均气温统计如图所示，那么在日平均气温这组数据中，中位数是（　　）

A．8 B．10 C．21 D．22
二、填空题（共7小题，每小题3分，满分21分）
11．已知关于x的方程x2＋mx＋4＝0有两个相等的实数根，则实数m的值是______．
12．如图，点D、E、F分别位于△ABC的三边上，满足DE∥BC，EF∥AB，如果AD：DB=3：2，那么BF：FC=_____．

13．二次函数的图象如图，若一元二次方程有实数根，则 的最大值为___

14．已知，大正方形的边长为4厘米，小正方形的边长为2厘米，起始状态如图所示，大正方形固定不动，把小正方形向右平移，当两个正方形重叠部分的面积为2平方厘米时，小正方形平移的距离为_____厘米．

15．计算﹣的结果为_____．
16．如图，小明在A时测得某树的影长为3米，B时又测得该树的影长为12米，若两次日照的光线互相垂直，则树的高度为_________米.

17．如图，矩形中，，，将矩形沿折叠，点落在点处.则重叠部分的面积为______.

三、解答题（共7小题，满分69分）
18．（10分）（1）如图1，正方形ABCD中，点E，F分别在边CD，AD上，AE⊥BF于点G，求证：AE=BF；
（2）如图2，矩形ABCD中，AB=2，BC=3，点E，F分别在边CD，AD上，AE⊥BF于点M，探究AE与BF的数量关系，并证明你的结论；
（3）在（2）的基础上，若AB=m，BC=n，其他条件不变，请直接写出AE与BF的数量关系；　 　．

19．（5分）如图，已知抛物线过点A（4，0），B（﹣2，0），C（0，﹣4）．
（1）求抛物线的解析式；
（2）在图甲中，点M是抛物线AC段上的一个动点，当图中阴影部分的面积最小值时，求点M的坐标；
（3）在图乙中，点C和点C1关于抛物线的对称轴对称，点P在抛物线上，且∠PAB=∠CAC1，求点P的横坐标．

20．（8分）如图，在中，,以边为直径作⊙交边于点,过点作于点，、的延长线交于点.
求证：是⊙的切线；若,且,求⊙的半径与线段的长.
21．（10分）“低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门抽样调查了某单位员工上下班的交通方式，绘制了如下统计图：

（1）填空：样本中的总人数为 ；开私家车的人数m= ；扇形统计图中“骑自行车”所在扇形的圆心角为 度；
（2）补全条形统计图；
（3）该单位共有2000人，积极践行这种生活方式，越来越多的人上下班由开私家车改为骑自行车．若步行，坐公交车上下班的人数保持不变，问原来开私家车的人中至少有多少人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数？
22．（10分）已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；如果△ABC是等边三角形，试求这个一元二次方程的根．
23．（12分）如图，平面直角坐标系xOy中，已知点A（0，3），点B（，0），连接AB，若对于平面内一点C，当△ABC是以AB为腰的等腰三角形时，称点C是线段AB的“等长点”．
（1）在点C1（﹣2，3+2），点C2（0，﹣2），点C3（3+，﹣）中，线段AB的“等长点”是点________；
（2）若点D（m，n）是线段AB的“等长点”，且∠DAB=60°，求点D的坐标；
（3）若直线y=kx+3k上至少存在一个线段AB的“等长点”，求k的取值范围．

24．（14分）（5分）计算：．



参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、C
【解析】
由题意满七进一，可得该图示为七进制数，化为十进制数为：1×73+3×72+2×7+6=510，
故选：C．
点睛：本题考查记数的方法，注意运用七进制转化为十进制，考查运算能力，属于基础题.
2、B
【解析】
根据同类二次根式才能合并可对A进行判断；根据二次根式的乘法对B进行判断；先把 化为最简二次根式，然后进行合并，即可对C进行判断；根据二次根式的除法对D进行判断．
【详解】
解：A、与不能合并，所以A选项不正确；
B、-=2−=，所以B选项正确；
C、×=，所以C选项不正确；
D、=÷=2÷=2，所以D选项不正确．
故选B．
【点睛】
此题考查二次根式的混合运算，注意先化简，再进一步利用计算公式和计算方法计算．
3、C
【解析】
如图，过点A作AM⊥DC于点M，过点B作BN⊥DC于点N．则AM=BN．通过解直角△ACM和△BCN分别求得CM、CN的长度，则易得AB =MN=CM﹣CN，即可得到结论．
【详解】
如图，过点A作AM⊥DC于点M，过点B作BN⊥DC于点N．
则AB=MN，AM=BN．
在直角△ACM中，∵∠ACM=45°，AM=50m，∴CM=AM=50m．
在直角△BCN中，∵∠BCN=∠ACB+∠ACD=60°，BN=50m，∴CN=（m），∴MN=CM﹣CN=50﹣（m）．
则AB=MN=（50﹣）m．
故选C．

【点睛】
本题考查了解直角三角形的应用．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
4、D
【解析】
根据正数都大于0，负数都小于0，两个负数绝对值大的反而小即可求解．
【详解】
∵正数大于0和一切负数，
∴只需比较-π和-1的大小，
∵|-π|＜|-1|，
∴最小的数是-1．
故选D．
【点睛】
此题主要考查了实数的大小的比较，注意两个无理数的比较方法：统一根据二次根式的性质，把根号外的移到根号内，只需比较被开方数的大小．
5、B
【解析】
由EB=CF，可得出EF=BC，又有∠A=∠D，本题具备了一组边、一组角对应相等，为了再添一个条件仍不能证明△ABC≌△DEF，那么添加的条件与原来的条件可形成SSA，就不能证明△ABC≌△DEF了．
【详解】
添加，根据AAS能证明≌，故A选项不符合题意．
B.添加与原条件满足SSA，不能证明≌，故B选项符合题意；
C.添加，可得，根据AAS能证明≌，故C选项不符合题意；
D.添加，可得，根据AAS能证明≌，故D选项不符合题意，
故选B．
【点睛】
本题考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL.注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
6、C
【解析】
∵∠C=90°，
∴cosA=，sinA= ，tanA=，cotA=，
∴c·cosA=b，c·sinA=a，b·tanA=a，a·cotA=b，
∴只有选项C正确，
故选C.
【点睛】本题考查了三角函数的定义，熟练掌握三角函数的定义并且灵活运用是解题的关键.
7、A
【解析】
根据任何一个一次函数都可以化为一个二元一次方程，再根据两个函数交点坐标就是二元一次方程组的解可直接得到答案．
【详解】
解：∵直线y1=k1x+b1与y2=k2x+b2的交点坐标为（2，4），
∴二元一次方程组的解为
故选A.
【点睛】
本题主要考查了函数解析式与图象的关系，满足解析式的点就在函数的图象上，在函数的图象上的点，就一定满足函数解析式．函数图象交点坐标为两函数解析式组成的方程组的解．
8、C
【解析】
根据等腰三角形的性质和勾股定理解答即可．
【详解】
解：∵点A，D分别对应数轴上的实数﹣2，2，
∴AD＝4，
∵等腰△ABC的底边BC与底边上的高AD相等，
∴BC＝4，
∴CD＝2，
在Rt△ACD中，AC＝，
故选：C．
【点睛】
此题考查等腰三角形的性质，注意等腰三角形的三线合一，熟练运用勾股定理．
9、B
【解析】
根据轴对称图形与中心对称图形的概念判断即可．
【详解】
解：A、是轴对称图形，也是中心对称图形，故错误；
B、是中心对称图形，不是轴对称图形，故正确；
C、是轴对称图形，也是中心对称图形，故错误；
D、是轴对称图形，也是中心对称图形，故错误．
故选B．
【点睛】
本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
10、D
【解析】
分析：根据条形统计图得到各数据的权，然后根据中位数的定义求解．
详解：一共30个数据，第15个数和第16个数都是22，所以中位数是22.
故选D.
点睛：考查中位数的定义，看懂条形统计图是解题的关键.

二、填空题（共7小题，每小题3分，满分21分）
11、±4
【解析】
分析：由方程有两个相等的实数根，得到根的判别式等于0，列出关于m的方程，求出方程的解即可得到m的值．
详解：∵方程有两个相等的实数根，
∴
解得：
故答案为
点睛：考查一元二次方程根的判别式，
当时，方程有两个不相等的实数根.
当时，方程有两个相等的实数根.
当时，方程没有实数根.
12、3:2
【解析】
因为DE∥BC,所以,因为EF∥AB,所以,所以,故答案为: 3:2.
13、3
【解析】
试题解析：：∵抛物线的开口向上，顶点纵坐标为-3，
∴a＞1．
-=-3，即b2=12a，
∵一元二次方程ax2+bx+m=1有实数根，
∴△=b2-4am≥1，即12a-4am≥1，即12-4m≥1，解得m≤3，
∴m的最大值为3，
14、1或5.
【解析】
小正方形的高不变，根据面积即可求出小正方形平移的距离．
【详解】
解：当两个正方形重叠部分的面积为2平方厘米时，重叠部分宽为2÷2＝1，
①如图，小正方形平移距离为1厘米；

②如图，小正方形平移距离为4+1＝5厘米．

故答案为1或5，
【点睛】
此题考查了平移的性质，要明确，平移前后图形的形状和面积不变．画出图形即可直观解答．
15、．
【解析】
根据同分母分式加减运算法则化简即可．
【详解】
原式＝，
故答案为．
【点睛】
本题考查了分式的加减运算，熟记运算法则是解题的关键．
16、1
【解析】
根据题意，画出示意图，易得：Rt△EDC∽Rt△FDC，进而可得；即DC2=ED?FD，代入数据可得答案．
【详解】
根据题意，作△EFC，

树高为CD，且∠ECF=90°，ED=3，FD=12，
易得：Rt△EDC∽Rt△DCF，
有，即DC2=ED×FD，
代入数据可得DC2=31，
DC=1，
故答案为1．
17、10
【解析】
根据翻折的特点得到，.设，则.在中，，即，解出x,再根据三角形的面积进行求解.
【详解】
∵翻折，∴，，
又∵，
∴，
∴.设，则.
在中，，即，
解得，
∴，
∴.
【点睛】
此题主要考查勾股定理，解题的关键是熟知翻折的性质及勾股定理的应用.

三、解答题（共7小题，满分69分）
18、（1）证明见解析；（2）AE=BF，（3）AE=BF；
【解析】
（1）根据正方形的性质，可得∠ABC与∠C的关系，AB与BC的关系，根据两直线垂直，可得∠AMB的度数，根据直角三角形锐角的关系，可得∠ABM与∠BAM的关系，根据同角的余角相等，可得∠BAM与∠CBF的关系，根据ASA，可得△ABE≌△BCF，根据全等三角形的性质，可得答案；（2）根据矩形的性质得到∠ABC=∠C，由余角的性质得到∠BAM=∠CBF，根据相似三角形的性质即可得到结论;（3）结论：AE=BF．证明方法类似（2）；
【详解】
（1）证明：

∵四边形ABCD是正方形，
∴∠ABC=∠C，AB=BC．
∵AE⊥BF，
∴∠AMB=∠BAM+∠ABM=90°，
∵∠ABM+∠CBF=90°，
∴∠BAM=∠CBF．
在△ABE和△BCF中，
，
∴△ABE≌△BCF（ASA），
∴AE=BF；
（2）解：如图2中，结论：AE=BF，

理由：∵四边形ABCD是矩形，
∴∠ABC=∠C，
∵AE⊥BF，
∴∠AMB=∠BAM+∠ABM=90°，
∵∠ABM+∠CBF=90°，
∴∠BAM=∠CBF，
∴△ABE∽△BCF，
∴，
∴AE=BF．
（3）结论：AE=BF．
理由：∵四边形ABCD是矩形，
∴∠ABC=∠C，
∵AE⊥BF，
∴∠AMB=∠BAM+∠ABM=90°，
∵∠ABM+∠CBF=90°，
∴∠BAM=∠CBF，
∴△ABE∽△BCF，
∴，
∴AE=BF．
【点睛】
本题考查了四边形综合题、相似三角形的判定和性质，全等三角形的判定和性质，正方形的性质，矩形的性质，熟练掌握全等三角形或相似三角形的判定和性质是解题的关键．
19、 (1)y＝x2－x－4(2)点M的坐标为(2，－4)(3)－或－
【解析】
【分析】(1)设交点式y=a(x+2)(x-4),然后把C点坐标代入求出a即可得到抛物线解析式; 
(2) 连接OM，设点M的坐标为.由题意知，当四边形OAMC面积最大时，阴影部分的面积最小．S四边形OAMC＝S△OAM＋S△OCM－(m－2)2＋12. 当m＝2时，四边形OAMC面积最大，此时阴影部分面积最小;
(3) 抛物线的对称轴为直线x＝1，点C与点C1关于抛物线的对称轴对称，所以C1(2，－4)．连接CC1，过C1作C1D⊥AC于D，则CC1＝2.先求AC＝4，CD＝C1D＝，AD＝4－＝3；设点P ，过P作PQ垂直于x轴，垂足为Q. 证△PAQ∽△C1AD，得，即，解得解得n＝－，或n＝－，或n＝4(舍去).
【详解】(1)抛物线的解析式为y＝ (x－4)(x＋2)＝x2－x－4.
(2)连接OM，设点M的坐标为.
由题意知，当四边形OAMC面积最大时，阴影部分的面积最小．
S四边形OAMC＝S△OAM＋S△OCM
＝× 4m＋× 4
＝－m2＋4m＋8＝－(m－2)2＋12.
当m＝2时，四边形OAMC面积最大，此时阴影部分面积最小，所以点M的坐标为(2，－4)．
(3)∵抛物线的对称轴为直线x＝1，点C与点C1关于抛物线的对称轴对称，所以C1(2，－4)．
连接CC1，过C1作C1D⊥AC于D，则CC1＝2.
∵OA＝OC，∠AOC＝90°，∠CDC1＝90°，
∴AC＝4，CD＝C1D＝，AD＝4－＝3，
设点P ，过P作PQ垂直于x轴，垂足为Q.
∵∠PAB＝∠CAC1，∠AQP＝∠ADC1，
∴△PAQ∽△C1AD，
∴，
即 ，化简得 ＝(8－2n)，
即3n2－6n－24＝8－2n，或3n2－6n－24＝－(8－2n)，
解得n＝－，或n＝－，或n＝4(舍去)，
∴点P的横坐标为－或－.
【点睛】本题考核知识点：二次函数综合运用. 解题关键点：熟记二次函数的性质，数形结合，由所求分析出必知条件.
20、（1）证明参见解析；（2）半径长为，=.
【解析】
（1）已知点D在圆上，要连半径证垂直，连结，则，所以，∵，∴.∴，∴∥.由得出，于是得出结论；（2）由得到，设，则.，，，由，解得值，进而求出圆的半径及AE长.
【详解】
解：（1）已知点D在圆上，要连半径证垂直，如图2所示，连结，∵，∴.∵，∴.∴，∴∥.∵，∴.∴是⊙的切线；（2）在和中，∵，∴. 设，则.∴，.∵，∴.∴，解得=，则3x=,AE=6×-=6,∴⊙的半径长为，=.

【点睛】
1.圆的切线的判定；2.锐角三角函数的应用.
21、（1）80，20，72；（2）16，补图见解析；（3）原来开私家车的人中至少有50人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数．
【解析】
试题分析：（1）用乘公交车的人数除以所占的百分比，计算即可求出总人数，再用总人数乘以开私家车的所占的百分比求出m，用360°乘以骑自行车的所占的百分比计算即可得解：
样本中的总人数为：36÷45%=80人；
开私家车的人数m=80×25%=20；
扇形统计图中“骑自行车”的圆心角为.
（2）求出骑自行车的人数，然后补全统计图即可.
（3）设原来开私家车的人中有x人改为骑自行车，表示出改后骑自行车的人数和开私家车的人数，列式不等式，求解即可．
试题解析：解：（1）80，20，72.
（2）骑自行车的人数为：80×20%=16人，
补全统计图如图所示；

（3）设原来开私家车的人中有x人改为骑自行车，
由题意得，，解得x≥50.
答：原来开私家车的人中至少有50人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数．
考点：1.条形统计图；2.扇形统计图；3.频数、频率和总量的关系；4.一元一次不等式的应用．
22、 (1) △ABC是等腰三角形；(2)△ABC是直角三角形；(3) x1=0，x2=﹣1．
【解析】
试题分析：（1）直接将x=﹣1代入得出关于a，b的等式，进而得出a=b，即可判断△ABC的形状；
（2）利用根的判别式进而得出关于a，b，c的等式，进而判断△ABC的形状；
（3）利用△ABC是等边三角形，则a=b=c，进而代入方程求出即可．
试题解析：（1）△ABC是等腰三角形；
理由：∵x=﹣1是方程的根，
∴（a+c）×（﹣1）2﹣2b+（a﹣c）=0，
∴a+c﹣2b+a﹣c=0，
∴a﹣b=0，
∴a=b，
∴△ABC是等腰三角形；
（2）∵方程有两个相等的实数根，
∴（2b）2﹣4（a+c）（a﹣c）=0，
∴4b2﹣4a2+4c2=0，
∴a2=b2+c2，
∴△ABC是直角三角形；
（3）当△ABC是等边三角形，∴（a+c）x2+2bx+（a﹣c）=0，可整理为：
2ax2+2ax=0，
∴x2+x=0，
解得：x1=0，x2=﹣1．
考点：一元二次方程的应用．
23、（1）C1，C3；（2）D（﹣，0）或D（，3）；（3）﹣≤k≤
【解析】
（1）直接利用线段AB的“等长点”的条件判断；
（2）分两种情况讨论，利用对称性和垂直的性质即可求出m，n；
（3）先判断出直线y=kx+3与圆A，B相切时，如图2所示，利用相似三角形的性质即可求出结论．
【详解】
（1）∵A（0，3），B（，0），
∴AB=2，
∵点C1（﹣2，3+2），
∴AC1==2，
∴AC1=AB，
∴C1是线段AB的“等长点”，
∵点C2（0，﹣2），
∴AC2=5，BC2==，
∴AC2≠AB，BC2≠AB，
∴C2不是线段AB的“等长点”，
∵点C3（3+，﹣），
∴BC3==2，
∴BC3=AB，
∴C3是线段AB的“等长点”；
故答案为C1，C3；
（2）如图1，

在Rt△AOB中，OA=3，OB=，
∴AB=2，tan∠OAB==，
∴∠OAB=30°，
当点D在y轴左侧时，
∵∠DAB=60°，
∴∠DAO=∠DAB﹣∠BAO=30°，
∵点D（m，n）是线段AB的“等长点”，
∴AD=AB，
∴D（﹣，0），
∴m=，n=0，
当点D在y轴右侧时，
∵∠DAB=60°，
∴∠DAO=∠BAO+∠DAB=90°，
∴n=3，
∵点D（m，n）是线段AB的“等长点”，
∴AD=AB=2，
∴m=2；
∴D（，3）
（3）如图2，

∵直线y=kx+3k=k（x+3），
∴直线y=kx+3k恒过一点P（﹣3，0），
∴在Rt△AOP中，OA=3，OP=3，
∴∠APO=30°，
∴∠PAO=60°，
∴∠BAP=90°，
当PF与⊙B相切时交y轴于F，
∴PA切⊙B于A，
∴点F就是直线y=kx+3k与⊙B的切点，
∴F（0，﹣3），
∴3k=﹣3，
∴k=﹣，
当直线y=kx+3k与⊙A相切时交y轴于G切点为E，
∴∠AEG=∠OPG=90°，
∴△AEG∽△POG，
∴，
∴=，解得：k=或k=（舍去）
∵直线y=kx+3k上至少存在一个线段AB的“等长点”，
∴﹣≤k≤，
【点睛】
此题是一次函数综合题，主要考查了新定义，锐角三角函数，直角三角形的性质，等腰三角形的性质，对称性，解（1）的关键是理解新定义，解（2）的关键是画出图形，解（3）的关键是判断出直线和圆A，B相切时是分界点．
24、．
【解析】
试题分析：利用负整数指数幂，零指数幂、绝对值、特殊角的三角函数值的定义解答．
试题解析：原式==．
考点：1．实数的运算；2．零指数幂；3．负整数指数幂；4．特殊角的三角函数值．