广东省学年汕头市潮阳区高一上期末数学试卷

广东省汕头市潮阳区20182019学年高一（上）期末数学试卷（解析版）

一、选择题（本大题共12小题，共60.0分）

1. 已知集合，集合，则　　

A.  B.
C. ， D.

【答案】A

【解析】解：；
．
故选：A．
可解出集合A，B，然后进行补集的运算即可．
考查描述法、区间表示集合的概念，对数函数的定义域，以及指数函数的单调性，补集的运算．
 

2. 在平面直角坐标系中，已知角始边与x轴非负半轴重合，顶点与原点重合，且终边上有一点P坐标为，则　　

A.  B.  C.  D. 1

【答案】C

【解析】解：已知角始边与x轴非负半轴重合，顶点与原点重合，且终边上有一点P坐标为，
则，，，
故选：C．
由题意利用任意角的三角函数的定义，求得．
本题主要考查任意角的三角函数的定义，属于基础题．
 

3. 设，，，则　　

A.  B.  C.  D.

【答案】B

【解析】解：由对数函数的图象和性质可得
，
由指数函数的图象和性质可得


故选：B．
根据对数函数的图象和性质可得，，根据指数函数的图象和性质可得，从而可得a、b、c的大小关系．
本题主要考查指对数函数的图象和性质在比较大小中的应用，一般来讲，考查函数的单调性，以及图象的分布，属中档题．
 

4. 若，则　　

A. 2 B.  C.  D. 17

【答案】B

【解析】解：，
．
故选：B．
由，，能求出结果．
本题考查函数值的求法，考查实数性质等基础知识，考查运算求解能力，是基础题．
 

5. 若向量，满足，当，不共线时，与的关系是　　

A. 相等 B. 平行 C. 垂直 D. 相交但不垂直

【答案】C

【解析】解：；
；
又不共线；
和都是非零向量；
．
故选：C．
根据即可得出，而根据题意可判断和都是非零向量，从而得出．
考查向量垂直的充要条件，以及向量数量积的运算，平面向量基本定理．
 

6. 下列函数中，在其定义域内是增函数而且又是奇函数的是　　

A.  B.  C.  D.

【答案】C

【解析】解：A虽增却非奇非偶，B、D是偶函数，
C由奇偶函数定义可知是奇函数，由复合函数单调性可知在其定义域内是增函数或 0)'/>，
故选：C．
根据函数奇偶性和单调性的定义和性质进行判断．
本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．
 

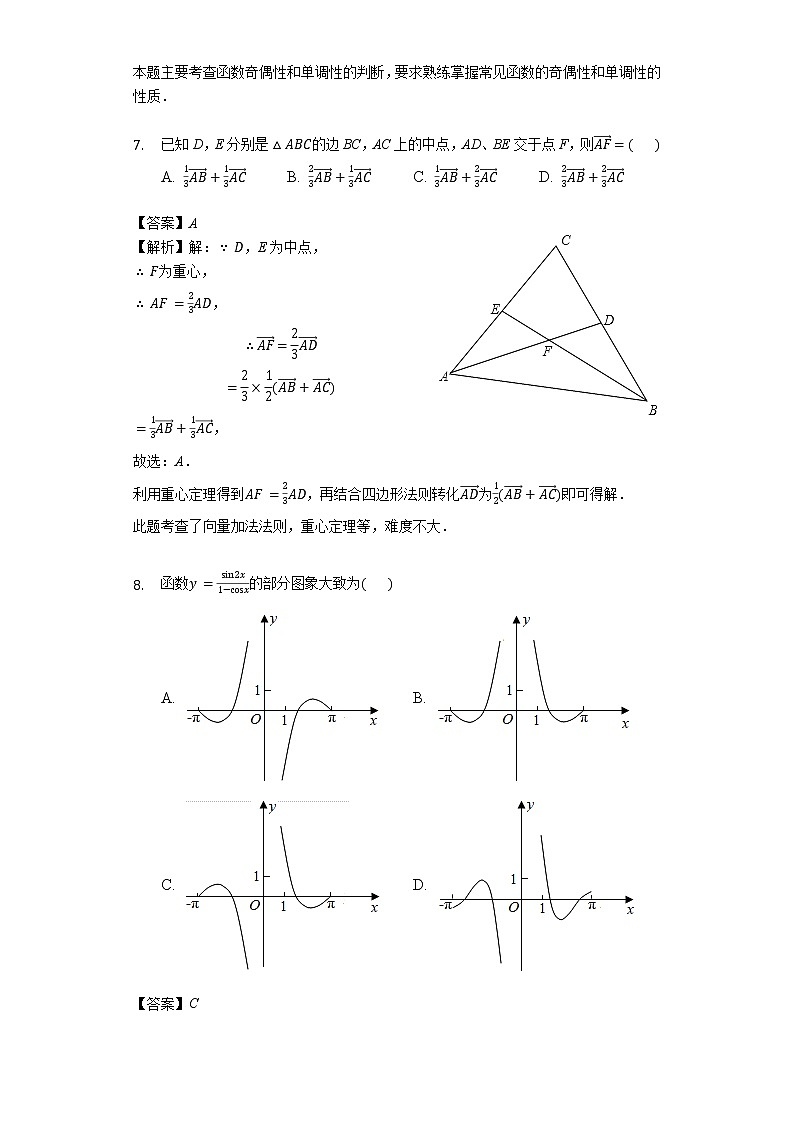
7. 已知D，E分别是的边BC，AC上的中点，AD、BE交于点F，则　　

A.  B.  C.  D.

【答案】A

【解析】解：，E为中点，
为重心，
，


，
故选：A．
利用重心定理得到，再结合四边形法则转化为即可得解．
此题考查了向量加法法则，重心定理等，难度不大．
 

8. 函数的部分图象大致为　　

A.  B.
C.  D.

【答案】C

【解析】解：函数，
可知函数是奇函数，排除选项B，
当时，，排除A，
时，，排除D．
故选：C．
判断函数的奇偶性排除选项，利用特殊值判断即可．
本题考查函数的图形的判断，三角函数化简，函数的奇偶性以及函数的特殊点是判断函数的图象的常用方法．
 

9. 设满足，且对任意，有，则　　

A.  B.
C.  D. 与不可比较

【答案】A

【解析】解：，，
，，即．
当时，，在上单调递减，
当时，，在上单调递增，
当时，，
综上，
故选：A．
由得出，由可知对称轴为，可求出，从而得出和的大小关系，结合的单调性得出结论．
本题考查了二次函数与指数函数的性质，比较和的大小关系和范围是关键．
 

10. 在直角三角形ABC中，，，对于平面ABC内的任一点M，平面ABC内总有一点D使得，则　　

A. 1 B. 2 C. 4 D. 6

【答案】D

【解析】解：对于平面ABC内的任一点，平面ABC内总有一点D使得，
即对于平面ABC内的任一点M，平面ABC内总有一点D使得
所以D为线段AB上的点且

所以
故选：D．
所以D为线段AB上的点且，再将转化为，后代入相乘即可．
本题考查了平面向量数量积的性质及其运算，属基础题．
 

11. 已知将函数的图象向右平移m个单位长度可得的图象，则正实数m的最小值为　　

A.  B.  C.  D.

【答案】D

【解析】解：将函数的图象至少向右平移个单位长度可得的图象，
则正实数m的最小值为，
故选：D．
利用函数的图象变换规律，诱导公式，得出结论．
本题主要考查函数的图象变换规律，诱导公式，属于基础题．
 

12. 在R上定义运算：，若使得成立，则实数a的取值范围是　　

A.  B.
C.  D.

【答案】A

【解析】解：由题知．
，使得不等式成立，
转化为函数的最大值大于1，
即成立，解之可得或．
故选：A．
先利用定义把整理成，结合题中不等式解集不是空集，可得函数的最大值大于1，由二次函数的性质得：成立，解之可得或．
本题考查了在新定义下对函数恒成立问题的应用关于新定义型的题，关键是理解定义，并会用定义来解题．
 

二、填空题（本大题共4小题，共20.0分）

13. 已知，则的值为______．

【答案】

【解析】解：，
，
故答案为：．
将所求关系式“切”化“弦”，将代入计算即可．
本题考查同角三角函数基本关系的运用，“切”化“弦”是关键，属于基础题．
 

14. 已知，且，则______．

【答案】7

【解析】解：，且，
当时，，无解；
当时，，解得．
综上，．
故答案为：7．
当时，；当时，由此能求出a．
本题考查实数值的求法，考查函数性质等基础知识，考查运算求解能力，是基础题．
 

15. 设M是线段BC的中点，点A在直线BC外，，，则______．

【答案】2

【解析】解：
以AB、AC为邻边作平行四边形，可得对角线AD与BC长度相等
因此，四边形ABDC为矩形
是线段BC的中点，
是斜边BC上的中线，可得
，得，即

故答案为：2
根据向量加法的平行四边形形法则和减法的三角形法则，可得以AB、AC为邻边的平行四边形ABDC为矩形，可得AM是斜边BC上的中线，可得，结合题中数据即可算出的值．
本题给出向量、满足的等式和向量的模，求另一个向量的模着重考查了向量的加法、减法法则和模的计算公式等知识，属于基础题．
 

16. 已知函数，若方程有四个不同的实数根，则实数的取值范围是______．

【答案】

【解析】解：函数，
函数的图象如图：方程有四个不同的实数根，
转化为，由4个交点．
可得．
故答案为：．
利用分段函数画出函数的图象，然后求解a的范围即可．
本题考查函数与方程的应用，考查数形结合以及计算能力．
 

三、解答题（本大题共6小题，共70.0分）

17. 已知点A在平面直角坐标系中的坐标为，平面向量，，且，，．
    求实数m，n及点B的坐标；
    求向量与向量夹角的余弦值．

【答案】解：，，
，
所以，因为，
所以，
所以；
由可知，．

【解析】根据得到，根据得到，从而得，再根据可得；
根据向量的夹角公式可求得．
本题考查了平面向量数量积的性质及其运算，属基础题．
 

18. 求值：；
    已知为第四象限角，且，求的值．

【答案】解：．
，
可得：，，
为第四象限角，．

【解析】通过对数的运算法则化简求解即可．
利用诱导公式化简求解即可．
本题考查对数运算法则的应用，诱导公式的应用，三角函数化简求值，考查计算能力．
 

19. 已知定义在R上的函数的最大值和最小值分别为m、n，且函数同时满足下面三个条件：
    相邻两条对称轴相距；；．
    求函数的解析式；
    求函数的单调递减区间及其对称轴；
    求函数在区间上的值域．

【答案】解：相邻两条对称轴相距，周期，
，又，，
又，，
，
由，可知，
即，，
解得，，
又，，

由，，
，
函数的单调性减区间为，．
由，得，，
解得，，
函数的对称轴为，．
，，

函数在区间上的值域为．

【解析】相邻两条对称轴相距，从而周期，求出，由，得，从而，由，求出，由此能求出．
由，，能求出函数的单调性减区间；由，能求出函数的对称轴．
由，得，由此能求出函数在区间上的值域．
本题考查三角函数的解析式、减区间、对称轴、值域的求法，考查三角函数的性质等基础知识，考查运算求解能力，是中档题．
 

20. 2016年汕头市开展了一场创文行动一直以来，汕头市部分市民文明素质有待提高、环境脏乱差现象突出、交通秩序混乱、占道经营和违章搭建问题严重，为了解决这一老大难问题，汕头市政府打了一场史无前例的“创文”仗，目的是全力改善汕头市环境、卫生道路、交通各方面不文明现象，同时争夺2020年“全国文明城市”称号随着创文活动的进行，我区生活环境得到了很大的改善，但因为违法出行的三轮车减少，市民出行偶有不便有一商人从中看到商机，打算开一家汽车租赁公司，他委托一家调查公司进行市场调查，调查公司的调查结果如表：

若他打算购入汽车100辆用于租赁业务，通过调查发现租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元由上表，他决定每辆车月租金定价满足：
为方便预测，月租金定价必须为50的整数倍；不低于3000元；定价必须使得公司每月至少能出租10辆汽车设租赁公司每辆车月租金定价为x元时，每月能出租的汽车数量为y辆．
按调查数据，请将y表示为关于x的函数．
当x何值时，租赁公司月收益最大？最大月收益是多少？

【答案】解：由表格可知，当定价为3000元时，能出租100辆，当定价每提升50元时能出租的车辆将减少1辆，
则，
令，得，得，得，
所以所求函数，，且，，
由知，租赁公司的月收益为，
则
，，
当时，取得最大值为307050，
即月租金定为4050时，租赁公司的月收益最大，最大月收益为307050元．

【解析】根据表示得到当定价为3000元时，能出租100辆，当定价每提升50元时能出租的车辆将减少1辆，根据变化关系，设出函数关系即可
利用配方法结合一元二次函数最值的性质进行求解
本题主要考查函数的应用问题，根据条件建立函数关系，利用一元二次函数对称轴与最值的关系是解决本题的关键．
 

21. 已知函数．
    若，求a的值．
    判断函数的奇偶性，并证明你的结论．
    求不等式的解集．

【答案】解：若，则，
得，
即，
则，．
函数的定义域为R，
，即函数是奇函数．
由不等式得，
，
在R上是增函数，
不等式等价为，
即，
即，
得．
即不等式的解集为．

【解析】根据条件建立方程进行求解即可
根据函数奇偶性的定义进行证明
利用函数奇偶性和单调性的性质将不等式进行转化求解即可
本题主要考查函数奇偶性和单调性的应用，结合函数单调性和奇偶性的定义，进行转化是解决本题的关键．
 

22. 已知函数．
    当时，求不等式的解集．
    讨论不等式的解集．

【答案】解：当时，，
由得，得，即，即不等式的解集为
由得，
即，
若，则不等式等价为得，得，
若，则不等式等价为，
令，则不等式等价为，
若，抛物线开口向上，有两个零点2，，
若，则，此时不等式的解为，即，得，
若，则，此时不等式的无解，
若，则，此时不等式的解为，即，得，
若，抛物线开口向下，有两个零点2，，且，
此时不等式的解为或，即或，得或，
综上若，不等式的解集为或，
若，不等式的解集为，
若，不等式的解集为，
若，不等式的解集为空集，
若，不等式的解集为

【解析】当时，先求出，结合一元二次不等式的解法进行求解即可
分别讨论a的取值范围，结合一元二次不等式的解法进行求解即可
本题主要考查不等式的解法，结合一元二次不等式的解法，利用分类讨论法是解决本题的关键．