

中考数学专题复习课:巧用隐形圆解动态几何问题 课件
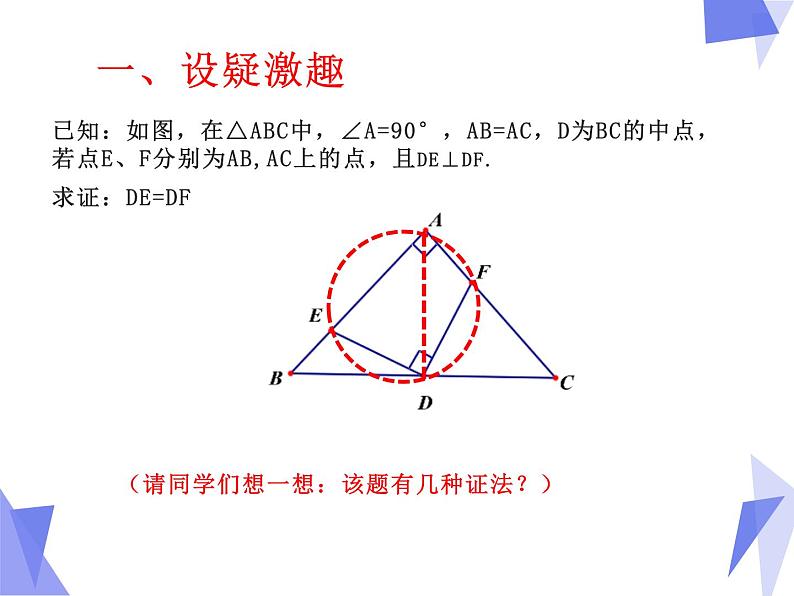
展开已知:如图,在△ABC中,∠A=90°,AB=AC,D为BC的中点,若点E、F分别为AB,AC上的点,且DE⊥DF.求证:DE=DF (请同学们想一想:该题有几种证法?)
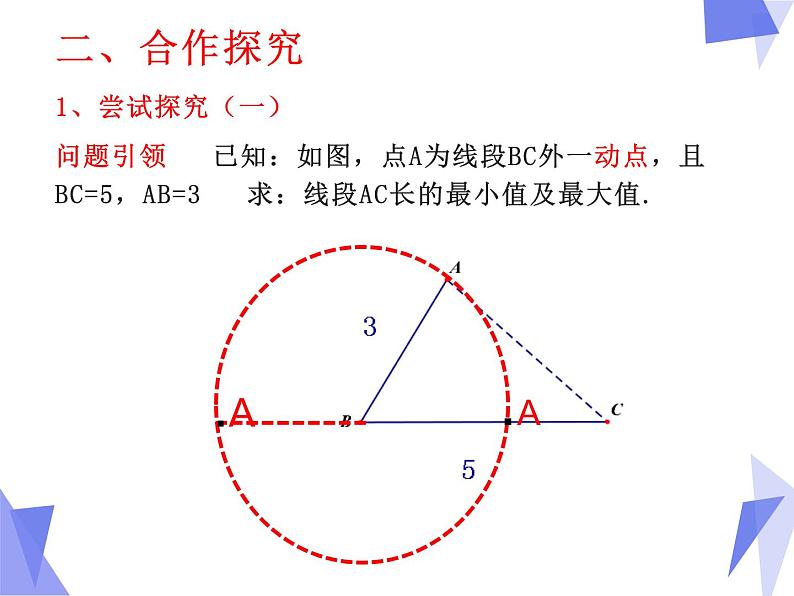
1、尝试探究(一)问题引领 已知:如图,点A为线段BC外一动点,且BC=5,AB=3 求:线段AC长的最小值及最大值.
动点P绕着定点O以定长OP旋转一周形成圆,简称“圆的动态定义模型”.
总结提升、 隐形圆模型一:
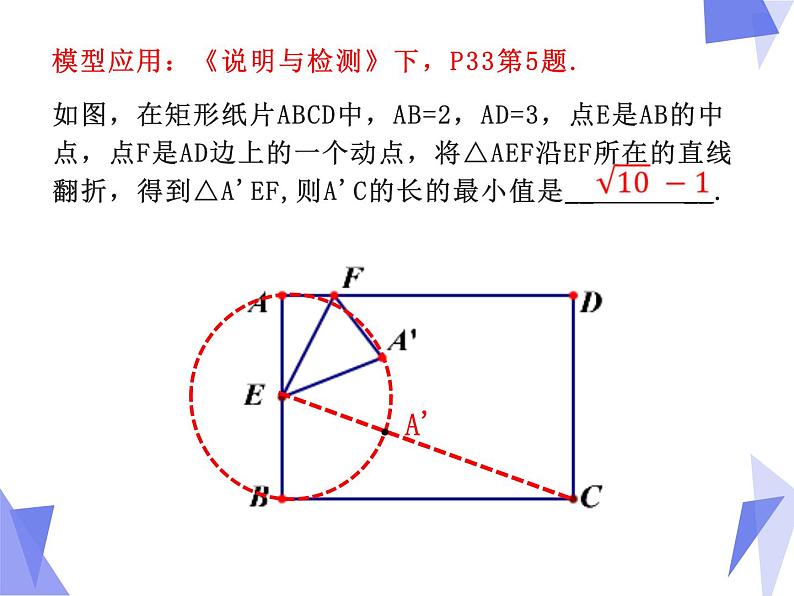
模型应用:《说明与检测》下,P33第5题.
如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在的直线翻折,得到△A'EF,则A'C的长的最小值是__ __.
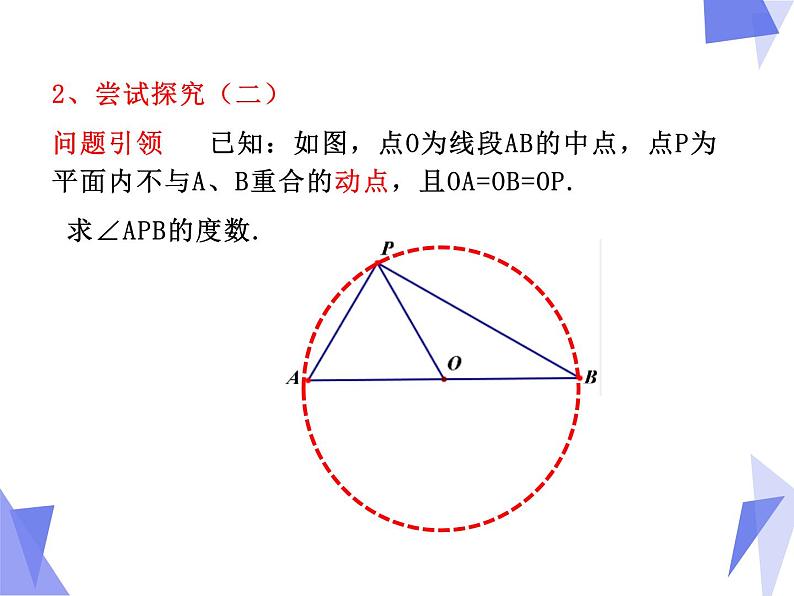
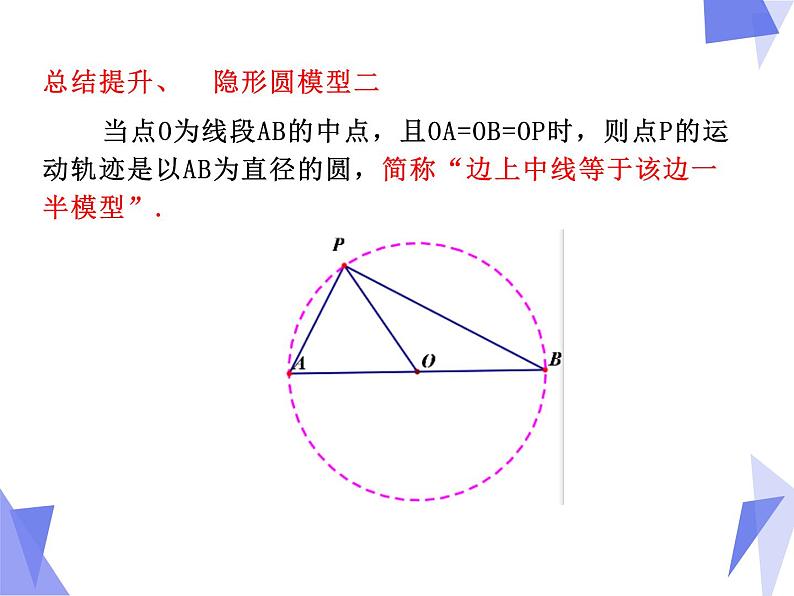
2、尝试探究(二)问题引领 已知:如图,点O为线段AB的中点,点P为平面内不与A、B重合的动点,且OA=OB=OP. 求∠APB的度数.
总结提升、 隐形圆模型二 当点O为线段AB的中点,且OA=OB=OP时,则点P的运动轨迹是以AB为直径的圆,简称“边上中线等于该边一半模型”.
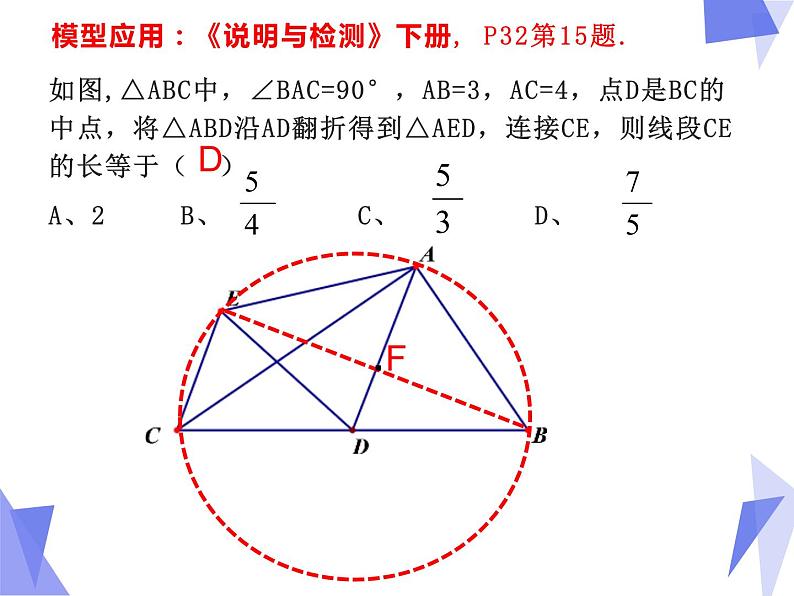
模型应用:《说明与检测》下册, P32第15题.
如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连接CE,则线段CE的长等于( )A、2 B、 C、 D、
3、尝试探究(三) 问题引领 如图:在Rt△ABC中,∠ACB=90°,且点C为动点,则点C的运动轨迹是什么?请说明理由.
总结提升、 隐形圆模型三 定线段AB所对角为直角,且直角顶点C为动点,则直角顶点C的运动轨迹是以线段AB为直径的圆(不与A、B重合),简称“直角三角形模型”.
模型应用:《说明与检测》下册, P73第15题.
4、尝试探究(四) 问题引领 如图:在四边形ABCD中,∠A=∠C=90°,则A、B、C、D四点共圆吗?请说明理由.
总结提升、隐形圆模型四 如图,在四边形ABCD中,当∠A=∠C=90°时,则A、B、C、D四点共圆. 一般地,当对角互补时,A、B、C、D四点仍共圆, 简称“四边形对角互补模型”.
模型应用:《说明与检测》下册,P34第10题
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC,交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为 .
5、尝试探究(五)问题引领 如图:在四边形ABCD中∠BAC=∠BDC=90°, 则A、B、C、D四点共圆吗?请说明理由.
总结提升、隐形圆模型五 如图,在四边形ABCD中,当∠BAC=∠BDC=90°时,则A、B、C、D四点共圆. 一般地,当∠BAC=∠BDC=α时,A、B、C、D四点仍共圆, 简称“X形同侧两等角模型”.
模型应用:《说明与检测》下册, P104第22题改编. 已知:如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4, CD⊥AB于点D,点E是AC延长线上一点,连接DE,过点D作FD⊥ED,交CB延长线于点F. 求 DE:DF
1.巧用隐形圆解动态几何题的三步曲:建模 造圆 用圆2.本节课主要渗透的数学思想是:(1) 模型思想;(2) 转化思想.
2、如图1,四边形ABCD是正方形,点E是AB边的中点,以AE为边作正方形AEFG,连接DE,BG。发现(1)线段DE,BG之间的数量关系是________ 直线DE,BG之间的位置关系是________探究(2)将图1中的正方形AEFG绕点A逆时针旋转至如图2所示的位置,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由。应用(3)如图3,将图1中的正方形AEDG绕点A逆时针旋转一周,记直线DE与BG的交点为P,若AB=6,请直接写出点P到CD所在直线的距离的最小值。
中考数学复习重难突破微专题(十一)隐形圆问题课件: 这是一份中考数学复习重难突破微专题(十一)隐形圆问题课件,共27页。
“隐形圆”点到圆最值问题-中考数学一轮复习课件: 这是一份“隐形圆”点到圆最值问题-中考数学一轮复习课件,共16页。PPT课件主要包含了引入定理,探究定理,应用定理,课堂检测,课堂小结等内容,欢迎下载使用。
中考数学二轮复习考点精讲课件专题40 几何最值之隐形圆问题【热点专题】 (含答案): 这是一份中考数学二轮复习考点精讲课件专题40 几何最值之隐形圆问题【热点专题】 (含答案),共13页。












