备战中考初中数学导练学案50讲—第25讲正方形（讲练版）

这是一份备战中考初中数学导练学案50讲—第25讲正方形（讲练版），共31页。学案主要包含了疑难点拨等内容，欢迎下载使用。

备战中考初中数学导练学案50讲
第25讲 正方形
【疑难点拨】
1．正方形的判定：①正方形既是有一组邻边相等的矩形，又是有一个角是直角的菱形；②既是矩形又是菱形的四边形是正方形；③正方形不仅是特殊的平行四边形，而且是特殊的矩形，还是特殊的菱形．
2．正方形的性质
正方形具有四边形、平行四边形、矩形、菱形的所有的性质．
(1)边的性质：正方形的四条边都相等，对边平行，邻边垂直；
(2)角的性质：正方形的四个角都是直角；
(3)对角线的性质：正方形的对角线互相垂直平分且相等，并且每条对角线平分一组对角．
正方形还有特殊性质：正方形的一条对角线把正方形分成两个全等的等腰直角三角形；两条对角线把正方形分成四个全等的等腰直角三角形；正方形是轴对称图形，有四条对称轴．
3．正方形的判定判定一个四边形是正方形的主要依据是定义，途径有两种：①先证明它是矩形，再证它有一组邻边相等；②先证明它是菱形，再证它有一个角是直角．
【基础篇】
一、选择题：
1. （2018·山东临沂·3分）如图，点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点．则下列说法：
①若AC=BD，则四边形EFGH为矩形；
②若AC⊥BD，则四边形EFGH为菱形；
③若四边形EFGH是平行四边形，则AC与BD互相平分；
④若四边形EFGH是正方形，则AC与BD互相垂直且相等．
其中正确的个数是（　　）

A．1 B．2 C．3 D．4
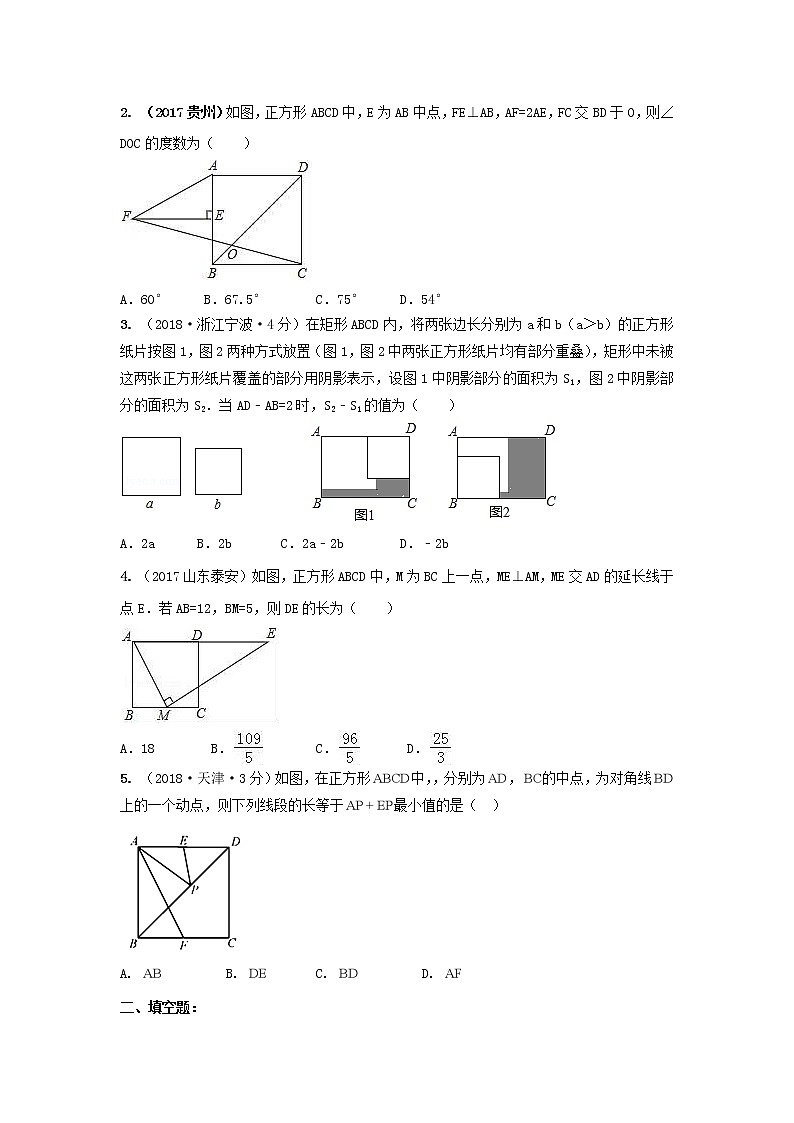
2. （2017贵州）如图，正方形ABCD中，E为AB中点，FE⊥AB，AF=2AE，FC交BD于O，则∠DOC的度数为（　　）

A．60° B．67.5° C．75° D．54°
3. （2018·浙江宁波·4分）在矩形ABCD内，将两张边长分别为a和b（a＞b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2．当AD﹣AB=2时，S2﹣S1的值为（　　）

A．2a B．2b C．2a﹣2b D．﹣2b
4. （2017山东泰安）如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交AD的延长线于点E．若AB=12，BM=5，则DE的长为（　　）

A．18 B． C． D．
5. （2018·天津·3分）如图，在正方形中，，分别为，的中点，为对角线上的一个动点，则下列线段的长等于最小值的是（ ）

A. B. C. D.
二、填空题：
6. （2017•新疆）如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为　3　s时，四边形EFGH的面积最小，其最小值是 cm2．

7. （2018·湖南省常德·3分）如图，将矩形ABCD沿EF折叠，使点B落在AD边上的点G处，点C落在点H处，已知∠DGH=30°，连接BG，则∠AGB=　 　．

8. （2018•江西•3分）在正方形ABCD中，AB=6，连接AC,BD,是正方形边上或对角线上一点，若PD=2AP，则AP的长为 .
三、解答与计算题：
9. （2018·浙江舟山·6分）如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF=45°。
求证：矩形ABCD是正方形







10. （2018·山东潍坊·8分）如图，点M是正方形ABCD边CD上一点，连接AM，作DE⊥AM于点E，BF⊥AM于点F，连接BE．
（1）求证：AE=BF；
（2）已知AF=2，四边形ABED的面积为24，求∠EBF的正弦值．






【能力篇】
一、选择题：
11. （2018四川省泸州市3分）如图，正方形ABCD中，E，F分别在边AD，CD上，AF，BE相交于点G，若AE=3ED，DF=CF，则的值是（　　）

A． B． C． D．







12. （2018·四川自贡·4分）如图，在边长为a正方形ABCD中，把边BC绕点B逆时针旋转60°，得到线段BM，连接AM并延长交CD于N，连接MC，则△MNC的面积为（　　）

A． B． C． D．
13. （2018年四川省南充市）如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE⊥AP于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF．下列结论正确的是（　　）

A．CE= B．EF= C．cos∠CEP= D．HF2=EF•CF
二、填空题：
14. （2018•广西桂林•3分）如图，矩形OABC的边AB与x轴交于点D，与反比例函数(k>0)在第一象限的图像交于点E，∠AOD=30°，点E的纵坐标为1，ΔODE的面积是，则k的值是________

15. （2018·山东青岛·3分）如图，已知正方形ABCD的边长为5，点E、F分别在AD、DC上，AE=DF=2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为　　．

三、解答与计算题：
16. （2017年江苏扬州）如图，将△ABC沿着射线BC方向平移至△A'B'C'，使点A'落在∠ACB的外角平分线CD上，连结AA'．
（1）判断四边形ACC'A'的形状，并说明理由；
（2）在△ABC中，∠B=90°，A B=24，cos∠BAC=，求CB'的长．





17. （2017四川眉山）如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交BC于G．
（1）求证：BG=DE；
（2）若点G为CD的中点，求的值．



18. （2018•株洲市）如图，在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD，其中AM=AN.
(1)求证：Rt△ABM≌Rt△AND
(2)线段MN与线段AD相交于T，若AT=,求的值




【探究篇】
19. （2017•黑龙江）在四边形ABCD中，对角线AC、BD交于点O．若四边形ABCD是正方形如图1：则有AC=BD，AC⊥BD．
旋转图1中的Rt△COD到图2所示的位置，AC′与BD′有什么关系？（直接写出）
若四边形ABCD是菱形，∠ABC=60°，旋转Rt△COD至图3所示的位置，AC′与BD′又有什么关系？写出结论并证明．









20. （2018•湖南省永州市•12分）如图1，在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，CD是边AB上的高，CD交GH于点I．若CI=4，HI=3，AD=．矩形DFGI恰好为正方形．

（1）求正方形DFGI的边长；
（2）如图2，延长AB至P．使得AC=CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？
（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M，N，求△MNG′的周长．


















第25讲 正方形
【疑难点拨】
1．正方形的判定：①正方形既是有一组邻边相等的矩形，又是有一个角是直角的菱形；②既是矩形又是菱形的四边形是正方形；③正方形不仅是特殊的平行四边形，而且是特殊的矩形，还是特殊的菱形．
2．正方形的性质
正方形具有四边形、平行四边形、矩形、菱形的所有的性质．
(1)边的性质：正方形的四条边都相等，对边平行，邻边垂直；
(2)角的性质：正方形的四个角都是直角；
(3)对角线的性质：正方形的对角线互相垂直平分且相等，并且每条对角线平分一组对角．
正方形还有特殊性质：正方形的一条对角线把正方形分成两个全等的等腰直角三角形；两条对角线把正方形分成四个全等的等腰直角三角形；正方形是轴对称图形，有四条对称轴．
3．正方形的判定判定一个四边形是正方形的主要依据是定义，途径有两种：①先证明它是矩形，再证它有一组邻边相等；②先证明它是菱形，再证它有一个角是直角．
【基础篇】
一、选择题：
1. （2018·山东临沂·3分）如图，点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点．则下列说法：
①若AC=BD，则四边形EFGH为矩形；
②若AC⊥BD，则四边形EFGH为菱形；
③若四边形EFGH是平行四边形，则AC与BD互相平分；
④若四边形EFGH是正方形，则AC与BD互相垂直且相等．
其中正确的个数是（　　）

A．1 B．2 C．3 D．4
【分析】因为一般四边形的中点四边形是平行四边形，当对角线BD=AC时，中点四边形是菱形，当对角线AC⊥BD时，中点四边形是矩形，当对角线AC=BD，且AC⊥BD时，中点四边形是正方形，
【解答】解：因为一般四边形的中点四边形是平行四边形，
当对角线BD=AC时，中点四边形是菱形，当对角线AC⊥BD时，中点四边形是矩形，当对角线AC=BD，且AC⊥BD时，中点四边形是正方形，
故④选项正确，
故选：A．
【点评】本题考查中点四边形、平行四边形、矩形、菱形的判定等知识，解题的关键是记住一般四边形的中点四边形是平行四边形，当对角线BD=AC时，中点四边形是菱形，当对角线AC⊥BD时，中点四边形是矩形，当对角线AC=BD，且AC⊥BD时，中点四边形是正方形．
2. （2017贵州）如图，正方形ABCD中，E为AB中点，FE⊥AB，AF=2AE，FC交BD于O，则∠DOC的度数为（　　）

A．60° B．67.5° C．75° D．54°
【考点】LE：正方形的性质．
【分析】如图，连接DF、BF．如图，连接DF、BF．首先证明∠FDB=∠FAB=30°，再证明△FAD≌△FBC，推出∠ADF=∠FCB=15°，由此即可解决问题．
【解答】解：如图，连接DF、BF．

∵FE⊥AB，AE=EB，
∴FA=FB，
∵AF=2AE，
∴AF=AB=FB，
∴△AFB是等边三角形，
∵AF=AD=AB，
∴点A是△DBF的外接圆的圆心，
∴∠FDB=∠FAB=30°，
∵四边形ABCD是正方形，
∴AD=BC，∠DAB=∠ABC=90°，∠ADB=∠DBC=45°，
∴∠FAD=∠FBC，
∴△FAD≌△FBC，
∴∠ADF=∠FCB=15°，
∴∠DOC=∠OBC+∠OCB=60°．
故选A．
3. （2018·浙江宁波·4分）在矩形ABCD内，将两张边长分别为a和b（a＞b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2．当AD﹣AB=2时，S2﹣S1的值为（　　）

A．2a B．2b C．2a﹣2b D．﹣2b
【考点】正方形的性质
【分析】利用面积的和差分别表示出S1和S2，然后利用整式的混合运算计算它们的差．
【解答】解：S1=（AB﹣a）•a+（CD﹣b）（AD﹣a）=（AB﹣a）•a+（AB﹣b）（AD﹣a），
S2=AB（AD﹣a）+（a﹣b）（AB﹣a），
∴S2﹣S1=AB（AD﹣a）+（a﹣b）（AB﹣a）﹣（AB﹣a）•a﹣（AB﹣b）（AD﹣a）=（AD﹣a）（AB﹣AB+b）+（AB﹣a）（a﹣b﹣a）=b•AD﹣ab﹣b•AB+ab=b（AD﹣AB）=2b．
故选：B．
【点评】本题考查了整式的混合运算：整体”思想在整式运算中较为常见，适时采用整体思想可使问题简单化，并且迅速地解决相关问题，此时应注意被看做整体的代数式通常要用括号括起来．也考查了正方形的性质．
4. （2017山东泰安）如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交AD的延长线于点E．若AB=12，BM=5，则DE的长为（　　）

A．18 B． C． D．
【考点】S9：相似三角形的判定与性质；KQ：勾股定理；LE：正方形的性质．
【分析】先根据题意得出△ABM∽△MCG，故可得出CG的长，再求出DG的长，根据△MCG∽△EDG即可得出结论．
【解答】解：∵四边形ABCD是正方形，AB=12，BM=5，
∴MC=12﹣5=7．
∵ME⊥AM，
∴∠AME=90°，
∴∠AMB+∠CMG=90°．
∵∠AMB+∠BAM=90°，
∴∠BAM=∠CMG，∠B=∠C=90°，
∴△ABM∽△MCG，
∴=，即=，解得CG=，
∴DG=12﹣=．
∵AE∥BC，
∴∠E=CMG，∠EDG=∠C，
∴△MCG∽△EDG，
∴=，即=，解得DE=．
故选B．

　
5. （2018·天津·3分）如图，在正方形中，，分别为，的中点，为对角线上的一个动点，则下列线段的长等于最小值的是（ ）

A. B. C. D.
【答案】D
【解析】分析：点E关于BD的对称点E′在线段CD上，得E′为CD中点，连接AE′，它与BD的交点即为点P，PA+PE的最小值就是线段AE′的长度；通过证明直角三角形ADE′≌直角三角形ABF即可得解．
详解：过点E作关于BD的对称点E′，连接AE′，交BD于点P．

∴PA+PE的最小值AE′；
∵E为AD的中点，
∴E′为CD的中点，
∵四边形ABCD是正方形，
∴AB=BC=CD=DA，∠ABF=∠AD E′=90°,
∴DE′=BF，
∴ΔABF≌ΔAD E′，
∴AE′=AF.
故选D.
点睛：本题考查了轴对称--最短路线问题、正方形的性质．此题主要是利用“两点之间线段最短”和“任意两边之和大于第三边”．因此只要作出点A（或点E）关于直线BD的对称点A′（或E′），再连接EA′（或AE′）即可．
二、填空题：
6. （2017•新疆）如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为　3　s时，四边形EFGH的面积最小，其最小值是　18　cm2．

【考点】H7：二次函数的最值；LE：正方形的性质．
【分析】设运动时间为t（0≤t≤6），则AE=t，AH=6﹣t，由四边形EFGH的面积=正方形ABCD的面积﹣4个△AEH的面积，即可得出S四边形EFGH关于t的函数关系式，配方后即可得出结论．
【解答】解：设运动时间为t（0≤t≤6），则AE=t，AH=6﹣t，
根据题意得：S四边形EFGH=S正方形ABCD﹣4S△AEH=6×6﹣4×t（6﹣t）=2t2﹣12t+36=2（t﹣3）2+18，
∴当t=3时，四边形EFGH的面积取最小值，最小值为18．
故答案为：3；18
【点评】本题考查了二次函数的最值、三角形以及正方形的面积，通过分割图形求面积法找出S四边形EFGH关于t的函数关系式是解题的关键．
7. （2018·湖南省常德·3分）如图，将矩形ABCD沿EF折叠，使点B落在AD边上的点G处，点C落在点H处，已知∠DGH=30°，连接BG，则∠AGB=　75°　．

【分析】由折叠的性质可知：GE=BE，∠EGH=∠ABC=90°，从而可证明∠EBG=∠EGB．，然后再根据∠EGH﹣∠EGB=∠EBC﹣∠EBG，即：∠GBC=∠BGH，由平行线的性质可知∠AGB=∠GBC，从而易证∠AGB=∠BGH，据此可得答案．
【解答】解：由折叠的性质可知：GE=BE，∠EGH=∠ABC=90°，
∴∠EBG=∠EGB．
∴∠EGH﹣∠EGB=∠EBC﹣∠EBG，即：∠GBC=∠BGH．
又∵AD∥BC，
∴∠AGB=∠GBC．
∴∠AGB=∠BGH．
∵∠DGH=30°，
∴∠AGH=150°，
∴∠AGB=∠AGH=75°，
故答案为：75°．
【点评】本题主要考查翻折变换，解题的关键是熟练掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
8. （2018•江西•3分）在正方形ABCD中，AB=6，连接AC,BD,是正方形边上或对角线上一点，若PD=2AP，则AP的长为 .
【解析】 本题考察动点问题，涉及直角三角形，辅助线，勾股定理，方程思想，综合性较强。

首先，要能判断符合条件的P点共有3个：如图1，PA=2 ；如图2，因为△APD是直角三角形，PD=2PA ,
所以∠PDA=30°，所以PA = 63=23 ；如图3，设PH= ,则PA= 2x,
PD=22x ,所以(6-x)2+x2=(22x)2 ,所以x=7-1 ,所以PA=14-2
【答案】 2，23 ，14-2 ★★★
三、解答与计算题：
9. （2018·浙江舟山·6分）如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF=45°。
求证：矩形ABCD是正方形
【考点】三角形全等的判定，矩形的性质，正方形的判定
【解析】【分析】证明矩形ABCD是正方形，根据有一组邻边相等的矩形是正方形，则可证一组邻边相等
【解答】∵四边形ABCD是矩形，
∴∠B=∠D=∠C=90°
∵△AEF是等边三角形
∴AE=AF，∠AEF=∠AFE=60°，
又∠CEF=45°，
∴∠CFE=∠CEF=45°，
∴∠AFD=∠AEB=180°-45°-60°=75°，
∴△AEB≌△AFD（AAS），
∴AB=AD,
∴矩形ABCD是正方形。
. 【点评】本题考查三角形全等的判定，矩形的性质，正方形的判定，属中档题.
10. （2018·山东潍坊·8分）如图，点M是正方形ABCD边CD上一点，连接AM，作DE⊥AM于点E，BF⊥AM于点F，连接BE．
（1）求证：AE=BF；
（2）已知AF=2，四边形ABED的面积为24，求∠EBF的正弦值．

【分析】（1）通过证明△ABF≌△DEA得到BF=AE；
（2）设AE=x，则BF=x，DE=AF=2，利用四边形ABED的面积等于△ABE的面积与△ADE的面积之和得到•x•x+•x•2=24，解方程求出x得到AE=BF=6，则EF=x﹣2=4，然后利用勾股定理计算出BE，最后利用正弦的定义求解．
【解答】（1）证明：∵四边形ABCD为正方形，
∴BA=AD，∠BAD=90°，
∵DE⊥AM于点E，BF⊥AM于点F，
∴∠AFB=90°，∠DEA=90°，
∵∠ABF+∠BAF=90°，∠EAD+∠BAF=90°，
∴∠ABF=∠EAD，
在△ABF和△DEA中
，
∴△ABF≌△DEA（AAS），
∴BF=AE；
（2）解：设AE=x，则BF=x，DE=AF=2，
∵四边形ABED的面积为24，
∴•x•x+•x•2=24，解得x1=6，x2=﹣8（舍去），
∴EF=x﹣2=4，
在Rt△BEF中，BE==2，
∴sin∠EBF===．
【点评】本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形具有四边形、平行四边形、矩形、菱形的一切性质．会运用全等三角形的知识解决线段相等的问题．也考查了解直角三角形．
【能力篇】
一、选择题：
11. （2018四川省泸州市3分）如图，正方形ABCD中，E，F分别在边AD，CD上，AF，BE相交于点G，若AE=3ED，DF=CF，则的值是（　　）

A． B． C． D．
【分析】如图作，FN∥AD，交AB于N，交BE于M．设DE=a，则AE=3a，利用平行线分线段成比例定理解决问题即可；
【解答】解：如图作，FN∥AD，交AB于N，交BE于M．

∵四边形ABCD是正方形，
∴AB∥CD，∵FN∥AD，
∴四边形ANFD是平行四边形，
∵∠D=90°，
∴四边形ANFD是解析式，
∵AE=3DE，设DE=a，则AE=3a，AD=AB=CD=FN=4a，AN=DF=2a，
∵AN=BN，MN∥AE，
∴BM=ME，
∴MN=a，
∴FM=a，
∵AE∥FM，
∴===，
故选：C．
【点评】本题考查正方形的性质、平行线分线段成比例定理、三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，学会利用参数解决问题，属于中考常考题型．
12. （2018·四川自贡·4分）如图，在边长为a正方形ABCD中，把边BC绕点B逆时针旋转60°，得到线段BM，连接AM并延长交CD于N，连接MC，则△MNC的面积为（　　）

A． B． C． D．
【分析】作MG⊥BC于G，MH⊥CD于H，根据旋转变换的性质得到△MBC是等边三角形，根据直角三角形的性质和勾股定理分别求出MH、CH，根据三角形的面积公式计算即可．
【解答】解：作MG⊥BC于G，MH⊥CD于H，
则BG=GC，AB∥MG∥CD，
∴AM=MN，
∵MH⊥CD，∠D=90°，
∴MH∥AD，
∴NH=HD，
由旋转变换的性质可知，△MBC是等边三角形，
∴MC=BC=a，
由题意得，∠MCD=30°，
∴MH=MC=a，CH=a，
∴DH=a﹣a，
∴CN=CH﹣NH=a﹣（a﹣a）=（﹣1）a，
∴△MNC的面积=××（﹣1）a=a2，
故选：C．

【点评】本题考查的是旋转变换的性质、正方形的性质，掌握正方形的性质、平行线的性质是解题的关键．
13. （2018年四川省南充市）如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE⊥AP于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF．下列结论正确的是（　　）

A．CE= B．EF= C．cos∠CEP= D．HF2=EF•CF
【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LE：正方形的性质；T7：解直角三角形．
【分析】首先证明BH=AH，推出EG=BG，推出CE=CB，再证明△ABC≌△CEH，Rt△HFE≌Rt△HFA，利用全等三角形的性质即可一一判断．
【解答】解：连接EH．

∵四边形ABCD是正方形，
∴CD=AB═BC=AD=2，CD∥AB，
∵BE⊥AP，CH⊥BE，
∴CH∥PA，
∴四边形CPAH是平行四边形，
∴CP=AH，
∵CP=PD=1，
∴EH=HB，∵HC⊥BE，
∴BG=EG，
∴CB=CE=2，故选项A错误，
∵CH=CH，CB=CE，HB=HE，
∴△ABC≌△CEH，
∴∠CBH=∠CEH=90°，
∵HF=HF，HE=HA，
∴Rt△HFE≌Rt△HFA，
∴AF=EF，设EF=AF=x，
在Rt△CDF中，有22+（2﹣x）2=（2+x）2，
∴x=，
∴EF=，故B错误，
∵PA∥CH，
∴∠CEP=∠ECH=∠BCH，
∴cos∠CEP=cos∠BCH==，故C错误．
∵HF=，EF=，FC=
∴HF2=EF•FC，故D正确，
故选：D．
【点评】本题考查正方形的性质、全等三角形的判定和性质、勾股定理、锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题．
二、填空题：
14. （2018•广西桂林•3分）如图，矩形OABC的边AB与x轴交于点D，与反比例函数(k>0)在第一象限的图像交于点E，∠AOD=30°，点E的纵坐标为1，ΔODE的面积是，则k的值是________

【答案】
【解析】分析：过E作EF⊥x轴，垂足为F，则EF=1，易求∠DEF=30°，从而DE=，根据ΔODE的面积是求出OD=，从而OF=3，所以k=3.
详解：过E作EF⊥x轴，垂足为F，

∵点E的纵坐标为1，
∴EF=1，
∵ΔODE的面积是
∴OD=，
∵四边形OABC是矩形，且∠AOD=30°,
∴∠DEF=30°,
∴DF=
∴OF=3，
∴k=3.
故答案为3.
点睛：本题考查了反比例函数解析式的求法，求出点E的坐标是解题关键.
15. （2018·山东青岛·3分）如图，已知正方形ABCD的边长为5，点E、F分别在AD、DC上，AE=DF=2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为　　．

【分析】根据正方形的四条边都相等可得AB=AD，每一个角都是直角可得∠BAE=∠D=90°，然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF，进一步得∠AGE=∠BGF=90°，从而知GH=BF，利用勾股定理求出BF的长即可得出答案．
【解答】解：∵四边形ABCD为正方形，
∴∠BAE=∠D=90°，AB=AD，
在△ABE和△DAF中，
∵，
∴△ABE≌△DAF（SAS），
∴∠ABE=∠DAF，
∵∠ABE+∠BEA=90°，
∴∠DAF+∠BEA=90°，
∴∠AGE=∠BGF=90°，
∵点H为BF的中点，
∴GH=BF，
∵BC=5、CF=CD﹣DF=5﹣2=3，
∴BF==，
∴GH=BF=，
故答案为：．
【点评】本题考查了正方形的性质，全等三角形的判定与性质，直角三角形两锐角互余等知识，掌握三角形全等的判定方法与正方形的性质是解题的关键．
三、解答与计算题：
16. （2017年江苏扬州）如图，将△ABC沿着射线BC方向平移至△A'B'C'，使点A'落在∠ACB的外角平分线CD上，连结AA'．
（1）判断四边形ACC'A'的形状，并说明理由；
（2）在△ABC中，∠B=90°，A B=24，cos∠BAC=，求CB'的长．

【考点】LO：四边形综合题；LA：菱形的判定与性质；Q2：平移的性质；T7：解直角三角形．
【分析】（1）根据平行四边形的判定定理（有一组对边平行且相等的四边形是平四边形）推知四边形ACC'A'是平行四边形．又对角线平分对角的平行四边形是菱形推知四边形ACC'A'是菱形．
（2）通过解直角△ABC得到AC、BC的长度，由（1）中菱形ACC'A'的性质推知AC=AA′，由平移的性质得到四边形ABB′A′是平行四边形，则AA′=BB′，所以CB′=BB′﹣BC．
【解答】解：（1）四边形ACC'A'是菱形．理由如下：
由平移的性质得到：AC∥A′C′，且AC=A′C′，
则四边形ACC'A'是平行四边形．
∴∠ACC′=∠AA′C′，
又∵CD平分∠ACB的外角，即CD平分∠ACC′，
∴CD也平分∠AA′C′，
∴四边形ACC'A'是菱形．

（2）∵在△ABC中，∠B=90°，A B=24，cos∠BAC=，
∴cos∠BAC==，即=，
∴AC=26．
∴由勾股定理知：BC===7．
又由（1）知，四边形ACC'A'是菱形，
∴AC=AA′=26．
由平移的性质得到：AB∥A′B′，AB=A′B′，则四边形ABB′A′是平行四边形，
∴AA′=BB′=26，
∴CB′=BB′﹣BC=26﹣7．

17. （2017四川眉山）如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交BC于G．
（1）求证：BG=DE；
（2）若点G为CD的中点，求的值．

【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LE：正方形的性质．
【分析】（1）由于BF⊥DE，所以∠GFD=90°，从而可知∠CBG=∠CDE，根据全等三角形的判定即可证明△BCG≌△DCE，从而可知BG=DE；
（2）设CG=1，从而知CG=CE=1，由勾股定理可知：DE=BG=，由易证△ABH∽△CGH，所以，从而可求出HG的长度，进而求出的值．
【解答】解：（1）∵BF⊥DE，
∴∠GFD=90°，
∵∠BCG=90°，∠BGC=∠DGF，
∴∠CBG=∠CDE，
在△BCG与△DCE中，

∴△BCG≌△DCE（ASA），
∴BG=DE，
（2）设CG=1，
∵G为CD的中点，
∴GD=CG=1，
由（1）可知：△BCG≌△DCE（ASA），
∴CG=CE=1，
∴由勾股定理可知：DE=BG=，
∵sin∠CDE==，
∴GF=，
∵AB∥CG，
∴△ABH∽△CGH，
∴=，
∴BH=，GH=，
∴=
18. （2018•株洲市）如图，在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD，其中AM=AN.
(1)求证：Rt△ABM≌Rt△AND
(2)线段MN与线段AD相交于T，若AT=,求的值

【答案】（1）证明见解析；（2）.
【解析】分析：（1）利用HL证明即可；
（2）证明△DNT∽△AMT，可得，由AT=AD，推出，在Rt△ABM中，tan∠ABM=．
详解：（1）∵AD=AB，AM=AN，∠AMB=∠AND=90°
∴Rt△ABM≌Rt△AND（HL）．
（2）由Rt△ABM≌Rt△AND易得：∠DAN=∠BAM，DN=BM
∵∠BAM+∠DAM=90°；∠DAN+∠ADN=90°
∴∠DAM=∠AND
∴ND∥AM
∴△DNT∽△AMT
∴
∵AT=AD，
∴
∵Rt△ABM
∴tan∠ABM=．
点睛：本题考查相似三角形的判定和性质、全等三角形的判定和性质、正方形的性质、解直角三角形等知识，解题的关键是灵活运用所学知识解决问题
【探究篇】
19. （2017•黑龙江）在四边形ABCD中，对角线AC、BD交于点O．若四边形ABCD是正方形如图1：则有AC=BD，AC⊥BD．
旋转图1中的Rt△COD到图2所示的位置，AC′与BD′有什么关系？（直接写出）
若四边形ABCD是菱形，∠ABC=60°，旋转Rt△COD至图3所示的位置，AC′与BD′又有什么关系？写出结论并证明．

【考点】LE：正方形的性质；KD：全等三角形的判定与性质；L8：菱形的性质；R2：旋转的性质．
【分析】图2：根据四边形ABCD是正方形，得到AO=OC，BO=OD，AC⊥BD，根据旋转的性质得到OD′=OD，OC′=OC，∠D′OD=∠C′OC，等量代换得到AO=BO，OC′=OD′，∠AOC′=∠BOD′，根据全等三角形的性质得到AC′=BD′，∠OAC′=∠OBD′，于是得到结论；
图3：根据四边形ABCD是菱形，得到AC⊥BD，AO=CO，BO=DO，求得OB=3OA，OD=3OC，根据旋转的性质得到OD′=OD，OC′=OC，∠D′OD=∠C′OC，求得OD′=3OC′，∠AOC′=∠BOD′，根据相似三角形的性质得到BD′=3AC′，于是得到结论．
【解答】解：图2结论：AC′=BD′，AC′⊥BD′，
理由：∵四边形ABCD是正方形，
∴AO=OC，BO=OD，AC⊥BD，
∵将Rt△COD旋转得到Rt△C′OD′，
∴OD′=OD，OC′=OC，∠D′OD=∠C′OC，
∴AO=BO，OC′=OD′，∠AOC′=∠BOD′，
在△AOC′与△BOD′中，&AO=BO&∠AOC'=∠BOD'&OC'=OD'，
∴△AOC′≌△BOD′，
∴AC′=BD′，∠OAC′=∠OBD′，
∵∠AO′D′=∠BO′O，∠O′BO+∠BO′O=90°，
∴∠O′AC′+∠AO′D′=90°，
∴AC′⊥BD′；
图3结论：BD′=3AC′，AC′⊥BD’
理由：∵四边形ABCD是菱形，
∴AC⊥BD，AO=CO，BO=DO，
∵∠ABC=60°，
∴∠ABO=30°，
∴OB=3OA，OD=3OC，
∵将Rt△COD旋转得到Rt△C′OD′，
∴OD′=OD，OC′=OC，∠D′OD=∠C′OC，
∴OD′=3OC′，∠AOC′=∠BOD′，
∴OBOA=OD'OC'=3，
∴△AOC′∽△BOD′，
∴BD'AC'=OBOA=3，∠OAC′=∠OBD′，
∴BD′=3AC′，
∵∠AO′D′=∠BO′O，∠O′BO+∠BO′O=90°，
∴∠O′AC′+∠AO′D′=90°，
∴AC′⊥BD′．

【点评】本题考查了正方形的性质，菱形的性质，全等三角形的判定和性质，相似三角形的判定和性质，旋转的性质，正确的识别图形是解题的关键．
20. （2018•湖南省永州市•12分）如图1，在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，CD是边AB上的高，CD交GH于点I．若CI=4，HI=3，AD=．矩形DFGI恰好为正方形．

（1）求正方形DFGI的边长；
（2）如图2，延长AB至P．使得AC=CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？
（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M，N，求△MNG′的周长．
【分析】（1）由HI∥AD，得到=，求出AD即可解决问题；
（2）如图2中，设等G落在PC时对应的点为G′，点F的对应的点为F′．求出IG′和BD的长比较即可判定；
（3）如图3中，如图将△DMI′绕点D逆时针旋转90°得到△DF′R，此时N、F′、R共线．想办法证明MN=MI′+NF′，即可解决问题；
【解答】解：（1）如图1中，

∵HI∥AD，
∴=，
∴=，
∴AD=6，
∴ID=CD﹣CI=2，
∴正方形的边长为2．
（2）如图2中，设等G落在PC时对应的点为G′，点F的对应的点为F′．

∵CA=CP，CD⊥PA，
∴∠ACD=∠PCD，∠A=∠P，
∵HG′∥PA，
∴∠CHG′=∠A，∠CG′H=∠P，
∴∠CHG′=∠CG′H，
∴CH=CG′，
∴IH=IG′=DF′=3，
∵IG∥DB，
∴=，
∴=，
∴DB=3，
∴DB=DF′=3，
∴点B与点F′重合，
∴移动后的矩形与△CBP重叠部分是△BGG′，
∴移动后的矩形与△CBP重叠部分的形状是三角形．

（3）如图3中，如图将△DMI′绕点D逆时针旋转90°得到△DF′R，此时N、F′、R共线．

∵∠MDN=∠NDF+∠MDI′=∠NDF′+∠DF′R=∠NDR=45°，
∵DN=DN，DM=DR，
∴△NDM≌△NDR，
∴MN=NR=NF′+RF′=NF′+MI′，
∴△MNG′的周长=MN+MG′+NG′=MG′+MI′+NG′+F′R=2I′G′=4．
【点评】本题考查四边形综合题、矩形的性质、正方形的性质、平行线等分线段定理、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用旋转法添加辅助线，构造全等三角形解决问题，属于中考压轴题．