

备战中考初中数学导练学案50讲—第17讲相交线与平行线(讲练版)
展开备战中考初中数学导练学案50讲
第17讲 相交线与平行线
【疑难点拨】
1. 利用对顶角、邻补角解决问题时要仔细观察图形 利用对顶角、邻补角解决问题,应注意图形中哪些是互补的角,哪些是对顶角,在解决问题时用到哪些对顶角和互补的角.
2. 证明两直线垂直的方法 垂直的定义为我们提供了一种证明垂直的方法和途径,若要证明两直线垂直,只需要证明两直线相交所成的四个角中有一个是直角即可.
3. 分离图形识别“三线八角” 对复杂图形中“三线八角”的识别,巧妙分离图形,简化图形是最有效的方法之一.同时,本题还可用其他方法解决.
4. “两点之间,线段最短”主要解决两点之间的距离最短问题;“垂线段最短”是解决点与直线距离最短的问题,通常过这个点作已知直线的垂线段,垂线段的长度就是最短距离.
5. 在解决与平行有关的问题时,要排除图形中其他线的干扰,分清由角的关系可判断哪两条直线平行,避免“张冠李戴”现象的发生.避免错误的方法是找出由两个角确定两条直线平行的基本图形,看清是哪两条直线被同一条直线所截形成的同位角相等或内错角相等,或同旁内角互补,才能判定是哪两条直线平行.
6. 由角定线:证明直线之间的关系的过程可用“由角定线”这四个字来概括,即通过说明某些角相等(或互补)来识别两直线平行.解题关键是角与线要找准对应关系.
7. 研究几何图形时要关注的两个方面 研究几何图形常常有两个方面的问题,一是要研究图形的“条件”,二是要研究图形的性质.
8. 平行线的性质与判定的综合运用:平行线的判定与性质中的因果关系是倒置的.平行线的判定是由角的数量关系来确定线的位置关系,平行线的性质是由线的位置关系来确定角的数量关系.对判定方法而言,“两直线平行”是结论,而对性质而言,“两直线平行”则是必不可少的前提条件.若先知道角,结论应是平行;若先知道平行,结论应是角相等或互补.
【基础篇】
一、选择题:
1. 如图,∠1与∠2是对顶角的是( )
A. B. C. D.
2. 在平面直角坐标系内,线段CD是由线段AB平移得到的,点A(﹣2,3)的对应点为C(2,5),则点B(﹣4,﹣1)的对应点D的坐标为( )
A.(﹣8,﹣3) B.(4,2) C.(0,1) D.(1,8)
3. 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2 C.∠D=∠DCE D.∠D+∠ACD=180°
4. 如图,面积为12cm 2 的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积为( )
A.24cm 2 B.36cm 2 C.48cm 2 D.无法确定
5. 如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
二、填空题:
6. 如果两个角是对顶角,那么这两个角相等,是 真 (真或假)命题,此命题的题设是 ,结论是 .
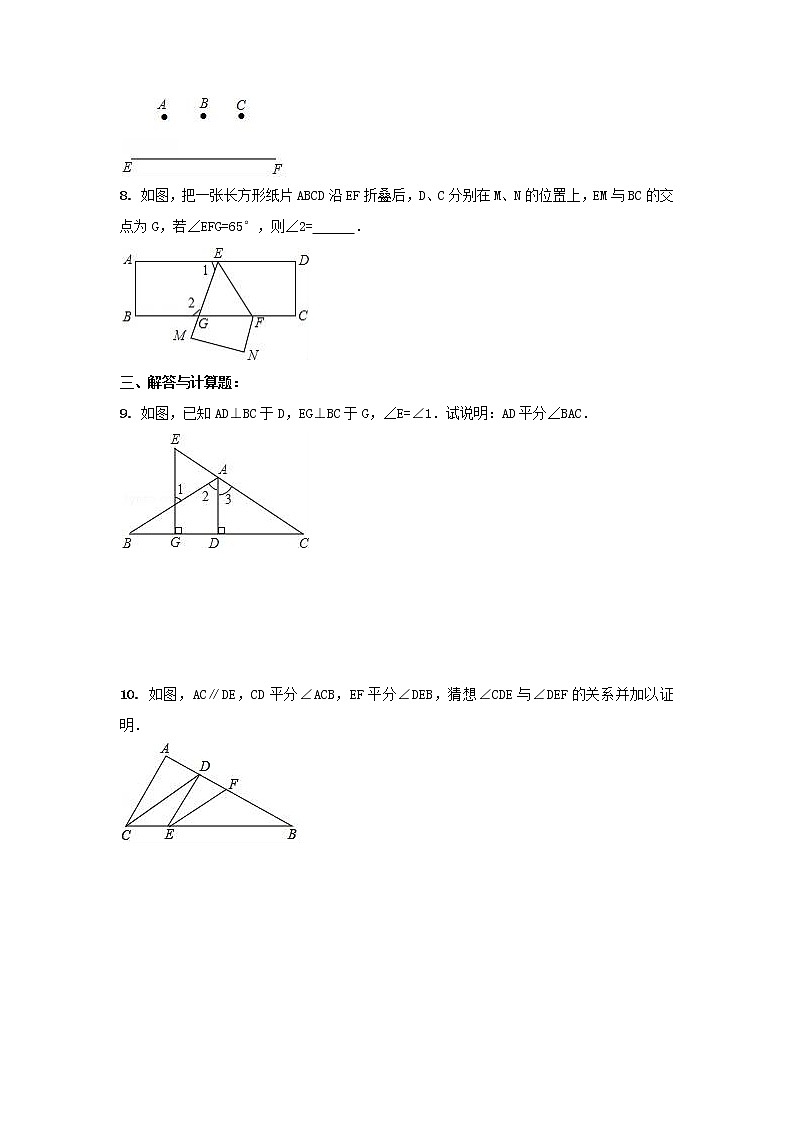
7. 如图,已知A,B,C三点及直线EF,过B点作AB∥EF,过B点作BC∥EF,那么A,B,C三点一定在同一条直线上,依据是 .
8. 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .
三、解答与计算题:
9. 如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1.试说明:AD平分∠BAC.
10. 如图,AC∥DE,CD平分∠ACB,EF平分∠DEB,猜想∠CDE与∠DEF的关系并加以证明.
【能力篇】
一、选择题:
11. 在5×5方格纸中将图(1)中的图形 N 平移后的位置如图(2)中所示,那么正确的平移方法是( )
A.先向下移动1格,再向左移动1格B.先向下移动2格,再向左移动2格
12. 已知:AB∥CD,∠ABE=120°,∠C=25°,则∠α度数为( )
A.60° B.75° C.85° D.80°
13. 一大门的栏杆如图所示,BA⊥AE,若CD∥AE,则∠ABC+∠BCD为( )度.
A.220° B.225° C.270° D.280°
二、填空题:
14. 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=80°,则∠GFD′= .
15. .如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是 (填序号).
三、解答与计算题:
16. 已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。
17. 如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?
(2、3小题只需选一题说明理由)
18. (1)问题发现
如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( )
∴∠C=∠CEF.( )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C= (等量代换)
即∠B+∠C=∠BEC.
(2)拓展探究
如果点E运动到图②所示的位置,其他条件不变,求证:∠B+∠C=360°﹣∠BEC.
(3)解决问题
如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(之间写出结论,不用写计算过程)
【探究篇】
19. 如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
20. 如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
第17讲 相交线与平行线
【疑难点拨】
1. 利用对顶角、邻补角解决问题时要仔细观察图形 利用对顶角、邻补角解决问题,应注意图形中哪些是互补的角,哪些是对顶角,在解决问题时用到哪些对顶角和互补的角.
2. 证明两直线垂直的方法 垂直的定义为我们提供了一种证明垂直的方法和途径,若要证明两直线垂直,只需要证明两直线相交所成的四个角中有一个是直角即可.
3. 分离图形识别“三线八角” 对复杂图形中“三线八角”的识别,巧妙分离图形,简化图形是最有效的方法之一.同时,本题还可用其他方法解决.
4. “两点之间,线段最短”主要解决两点之间的距离最短问题;“垂线段最短”是解决点与直线距离最短的问题,通常过这个点作已知直线的垂线段,垂线段的长度就是最短距离.
5. 在解决与平行有关的问题时,要排除图形中其他线的干扰,分清由角的关系可判断哪两条直线平行,避免“张冠李戴”现象的发生.避免错误的方法是找出由两个角确定两条直线平行的基本图形,看清是哪两条直线被同一条直线所截形成的同位角相等或内错角相等,或同旁内角互补,才能判定是哪两条直线平行.
6. 由角定线:证明直线之间的关系的过程可用“由角定线”这四个字来概括,即通过说明某些角相等(或互补)来识别两直线平行.解题关键是角与线要找准对应关系.
7. 研究几何图形时要关注的两个方面 研究几何图形常常有两个方面的问题,一是要研究图形的“条件”,二是要研究图形的性质.
8. 平行线的性质与判定的综合运用:平行线的判定与性质中的因果关系是倒置的.平行线的判定是由角的数量关系来确定线的位置关系,平行线的性质是由线的位置关系来确定角的数量关系.对判定方法而言,“两直线平行”是结论,而对性质而言,“两直线平行”则是必不可少的前提条件.若先知道角,结论应是平行;若先知道平行,结论应是角相等或互补.
【基础篇】
一、选择题:
1. 如图,∠1与∠2是对顶角的是( )
A. B. C. D.
【解答】解:A、∠1与∠2有一条边在同一条直线上,另一条边不在同一条直线上,不是对顶角,故A选项错误;
B、∠1与∠2没有公共顶点,不是对顶角,故B选项错误;
C、∠1与∠2的两边互为反向延长线,是对顶角,故C选项正确;
D、∠1与∠2有一条边在同一条直线上,另一条边不在同一条直线上,不是对顶角,故D选项错误.
故选:C.
2. 在平面直角坐标系内,线段CD是由线段AB平移得到的,点A(﹣2,3)的对应点为C(2,5),则点B(﹣4,﹣1)的对应点D的坐标为( )
A.(﹣8,﹣3) B.(4,2) C.(0,1) D.(1,8)
【考点】Q3:坐标与图形变化﹣平移.
【分析】根据点A(﹣2,3)的对应点为C(2,5),可知横坐标由﹣2变为2,向又移动了4个单位,3变为5,表示向上移动了2个单位,以此规律可得D的对应点的坐标.
【解答】解:点A(﹣2,3)的对应点为C(2,5),可知横坐标由﹣2变为2,向右移动了4个单位,3变为5,表示向上移动了2个单位,
于是B(﹣4,﹣1)的对应点D的横坐标为﹣4+4=0,点D的纵坐标为﹣1+2=1,
故D(0,1).
故选C.
3. 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2 C.∠D=∠DCE D.∠D+∠ACD=180°
【解答】解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
4. 如图,面积为12cm 2 的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积为( )
A.24cm 2 B.36cm 2 C.48cm 2 D.无法确定
答案: B
解析:由题意可知根据平移的性质可以知道四边形ACED的面积是三个△ABC的面积,依此计算即可.
∵平移的距离是边BC长的两倍,
∴BC=CE=EF,
∴四边形ACED的面积是三个△ABC的面积;
∴四边形ACED的面积=12×3=36cm 2 .
5. 如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
【解答】解:A、正确,符合内错角相等,两条直线平行的判定定理;
B、正确,符合同位角相等,两条直线平行的判定定理;
C、错误,若∠3=∠4,则AD∥BE;
D、正确,符合同旁内角互补,两条直线平行的判定定理;
故选C.
二、填空题:
6. 如果两个角是对顶角,那么这两个角相等,是 真 (真或假)命题,此命题的题设是 两个角是对顶角 ,结论是 这两个角相等 .
【解答】解:如果两个角是对顶角,那么这两个角相等,是真命题,此命题的题设是两个角是对顶角,结论是这两个角相等;
故答案为:是,两个角是对顶角,这两个角相等.
7. 如图,已知A,B,C三点及直线EF,过B点作AB∥EF,过B点作BC∥EF,那么A,B,C三点一定在同一条直线上,依据是 过直线外一点,有且只有一条直线与已知直线平行 .
【考点】J8:平行公理及推论.
【分析】根据过直线外一点,有且只有一条直线与已知直线平行可得A、B、C三点在同一条直线上.
【解答】解:A、B、C三点在同一条直线上,
∵AB∥EF,BC∥EF,
∴A、B、C三点在同一条直线上(过直线外一点,有且只有一条直线与已知直线平行).
故答案为:过直线外一点,有且只有一条直线与已知直线平行.
8. 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .
【考点】JA:平行线的性质.
【分析】据两直线平行,内错角相等求出∠3,再根据翻折的性质以及平角等于180°,求出∠1,然后根据两直线平行,同旁内角互补,列式计算即可得解.
【解答】解:∵长方形纸片ABCD的边AD∥BC,
∴∠3=∠EFG=65°,
根据翻折的性质,可得∠1=180°﹣2∠3=180°﹣2×65°=50°,
又∵AD∥BC,
∴∠2=180°﹣∠1=180°﹣50°=130°.
故答案为:130°.
三、解答与计算题:
9. 如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1.试说明:AD平分∠BAC.
【解答】解:∵AD⊥BC于D,EG⊥BC于G,
∴∠ADC=∠EGC=90°,
∴AD∥EG,
∴∠1=∠2,∠E=∠3.
又∵∠E=∠1,
∴∠2=∠3,
∴AD平分∠BAC.
10. 如图,AC∥DE,CD平分∠ACB,EF平分∠DEB,猜想∠CDE与∠DEF的关系并加以证明.
【考点】JA:平行线的性质;IJ:角平分线的定义.
【分析】根据平行线的性质,得出∠ACB=∠DEB,∠ACD=∠CDE,再根据角平分线的定义,得到∠ACD=∠ACB=∠DEB=∠DEF,即可得到∠CDE=∠DEF.
【解答】解:∠CDE=∠DEF.
证明:∵AC∥DE,
∴∠ACB=∠DEB,∠ACD=∠CDE,
∵CD平分∠ACB,EF平分∠DEB,
∴∠ACD=∠ACB=∠DEB=∠DEF,
∴∠CDE=∠DEF.
【能力篇】
一、选择题:
11. 在5×5方格纸中将图(1)中的图形 N 平移后的位置如图(2)中所示,那么正确的平移方法是( )
A.先向下移动1格,再向左移动1格B.先向下移动2格,再向左移动2格
C.先向下移动2格,再向左移动1格D.先向下移动1格,再向左移动2格
答案:C
解析: 图形的平移可以分成两步,先向左右平移,然后上下平移,或者先上下平移,然后左右平移.由图上看出, N 是先向下平移2格,再向左平移1格到图2的位置的.选C.
12. 已知:AB∥CD,∠ABE=120°,∠C=25°,则∠α度数为( )
A.60° B.75° C.85° D.80°
【解答】解:过E作EF∥CD,
∴∠C=∠FEC(两直线平行,内错角相等),
∴∠FEC=25°,
∵AB∥CD(已知),
∴EF∥AB(平行于同一直线的两直线平行),
∴∠B+∠BEF=180°(两直线平行,同旁内角互补),
∴∠BEF=60°,
∴∠α=∠BEF+∠FEC=85°,
故选C
13. 一大门的栏杆如图所示,BA⊥AE,若CD∥AE,则∠ABC+∠BCD为( )度.
A.220° B.225° C.270° D.280°
【考点】平行线的性质.
【分析】首先过点B作BF∥AE,易得∠BAE+∠ABC+∠BCD=360°,又由BA⊥AE,即可求得∠ABC+∠BCD的值.
【解答】解:过点B作BF∥AE,
∵CD∥AE,
∴CD∥BF∥AE,
∴∠BCD+∠CBF=180°,∠ABF+∠BAE=180°,
∴∠BAE+∠ABF+∠CBF+∠BCD=360°,
即∠BAE+∠ABC+∠BCD=360°,
∵BA⊥AE,
∴∠BAE=90°,
∴∠ABC+∠BCD=270°.
故答案为:270.故选C。
二、填空题:
14. 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=80°,则∠GFD′= .
【解答】解:矩形纸片ABCD中,AD∥BC,
∵∠CEF=80°,
∴∠EFG=∠CEF=80°,
∴∠EFD=180°﹣80°=100°,
根据折叠的性质,∠EFD′=∠EFD=100°,
∴∠GFD′=∠EFD′﹣∠EFG,
=100°﹣80°,
=20°.
故答案为:20°.
15. .如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是 (填序号).
【考点】同位角、内错角、同旁内角.
【分析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角作答.
【解答】解:①由同位角的概念得出:∠A与∠1是同位角;
②由同旁内角的概念得出:∠A与∠B是同旁内角;
③由内错角的概念得出:∠4与∠1不是内错角,错误;
④由内错角的概念得出:∠1与∠3是内错角,错误.
故正确的有2个,是①②.
故答案为:①②.
【点评】本题考查了同位角、内错角、同旁内角的概念.三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.
三、解答与计算题:
20. 16. 已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。
答案: (1)40°;(2)不变化,1:2;(3)60°,理由见解析.
解析:根据两直线平行,同旁内角互补求出∠AOC,然后求出∠EOB= ∠AOC,计算即可得解;
(2)根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠OFC=2∠OBC,从而得解;
(3)根据三角形的内角和定理求出∠COE=∠AOB,从而得到OB、OE、OF是∠AOC的四等分线,再利用三角形的内角和定理列式计算即可得解.
试题解析:(1)∵CB∥OA,
∴∠AOC=180°-∠C=180°-100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB= ∠AOC= ×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE= ∠AOC= ×80°=20°,
∴∠OEC=180°-∠C-∠COE=180°-100°-20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
17. 如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?
(2、3小题只需选一题说明理由)
【考点】JB:平行线的判定与性质.
【分析】(1)先根据CE平分∠ACD,AE平分∠BAC得出∠BAC=2∠EAC,∠ACD=2∠ACE,再由∠EAC+∠ACE=90°可知∠BAC+∠ACD=180,故可得出结论;
(2)过E作EF∥AB,根据平行线的性质可知EF∥AB∥CD,∠BAE=∠AEF,∠FEC=∠DCE,故∠BAE+∠ECD=90°,再由∠MCE=∠ECD即可得出结论;
(3)根据AB∥CD可知∠BAC+∠ACD=180°,∠QPC+∠PQC+∠PCQ=180°,故∠BAC=∠PQC+∠QPC.
【解答】解:(1)∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAE+∠MCD=90°;
过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠E=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD,
∴∠BAE+∠MCD=90°;
(3)∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠QPC+∠PQC+∠PCQ=180°,
∴∠BAC=∠PQC+∠QPC.
18. (1)问题发现
如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( 平行于同一直线的两直线平行 )
∴∠C=∠CEF.( 两直线平行,内错角相等 )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C= ∠BEF+∠CEF (等量代换)
即∠B+∠C=∠BEC.
(2)拓展探究
如果点E运动到图②所示的位置,其他条件不变,求证:∠B+∠C=360°﹣∠BEC.
(3)解决问题
如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= 20° .(之间写出结论,不用写计算过程)
【解答】(1)证明:如图①,过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C=∠CEF.(两直线平行,内错角相等),
∵EF∥AB,
∴∠B=∠BEF(同理),
∴∠B+∠C=∠BEF+∠CEF(等量代换)
即∠B+∠C=∠BEC,
故答案为:平行于同一直线的两直线平行,两直线平行,内错角相等,∠BEF+∠CEF;
(2)证明:如图②,过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
∴∠B+∠C+∠AEC=360°,
∴∠B+∠C=360°﹣∠BEC;
(3)解:如图③,过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C+∠CEF=180°,∠A=∠BEF,
∵∠C=120°,∠AEC=80°,
∴∠CEF=180°﹣120°=60°,
∴∠BEF=80°﹣60°=20°,
∴∠A=∠BEF=20°.
故答案为:20°.
【探究篇】
19. 如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
【考点】JB:平行线的判定与性质.
【分析】(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补,所以易证AB∥CD;
(2)利用(1)中平行线的性质推知°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件GH⊥EG,易证PF∥GH;
(3)利用三角形外角定理、三角形内角和定理求得∠4=90°﹣∠3=90°﹣2∠2;然后由邻补角的定义、角平分线的定义推知∠QPK=∠EPK=45°+∠2;最后根据图形中的角与角间的和差关系求得∠HPQ的大小不变,是定值45°.
【解答】解:(1)如图1,∵∠1与∠2互补,
∴∠1+∠2=180°.
又∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)如图2,由(1)知,AB∥CD,
∴∠BEF+∠EFD=180°.
又∵∠BEF与∠EFD的角平分线交于点P,
∴∠FEP+∠EFP=(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF.
∵GH⊥EG,
∴PF∥GH;
(3)∠HPQ的大小不发生变化,理由如下:
如图3,∵∠1=∠2,
∴∠3=2∠2.
又∵GH⊥EG,
∴∠4=90°﹣∠3=90°﹣2∠2.
∴∠EPK=180°﹣∠4=90°+2∠2.
∵PQ平分∠EPK,
∴∠QPK=∠EPK=45°+∠2.
∴∠HPQ=∠QPK﹣∠2=45°,
∴∠HPQ的大小不发生变化,一直是45°.
20. 如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
【解答】解:(1)∵(a+2)2+=0,
∴a+2=0,b﹣2=0,
∴a=﹣2,b=2,
∴A(﹣2,0),C(2,2).
∵CB⊥AB,∴B(2,0),
∴AB=4,CB=2,则S三角形ABC=×4×2=4.
(2)如图甲,过E作EF∥AC.
∵CB⊥x轴,
∴CB∥y轴,∠CBA=90°,
∴∠ODB=∠6.
又∵BD∥AC,
∴∠CAB=∠5,
∴∠CAB+∠ODB=∠5+∠6=180°﹣∠CBA=90°.
∵BD∥AC,
∴BD∥AC∥EF,
∴∠1=∠3,∠2=∠4.
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=∠CAB,∠4=∠ODB,
∴∠AED=∠1+∠2=∠3+∠4=(∠CAB+∠ODB)=45°.
(3)①当P在y轴正半轴上时,如图乙.
设点P(0,t),分别过点P,A,B作MN∥x轴,AN∥y轴,BM∥y轴,交于点M,N,则AN=t,CM=t﹣2,MN=4,PM=PN=2.
∵S三角形ABC=4,
∴S三角形ACP=S梯形MNAC﹣S三角形ANP﹣S三角形CMP=4,
∴×4(t﹣2+t)﹣×2t﹣×2(t﹣2)=4,解得t=3,即点P的坐标为(0,3).
②当P在y轴负半轴上时,如图丙,同①作辅助线.
设点P(0,a),则AN=﹣a,CM=﹣a+2,PM=PN=2.
∵S三角形ACP=S梯形MNAC﹣S三角形ANP﹣S三角形CMP=4,
∴×4(﹣a+2﹣a)﹣×2•(﹣a)﹣×2(2﹣a)=4,
解得a=﹣1,
∴点P的坐标为(0,﹣1).
综上所述,P点的坐标为(0,﹣1)或(0,3).
备战中考初中数学导练学案50讲—第48讲 尺规作图(讲练版): 这是一份备战中考初中数学导练学案50讲—第48讲 尺规作图(讲练版),共29页。学案主要包含了疑难点拨等内容,欢迎下载使用。
备战中考初中数学导练学案50讲—第40讲动态问题(讲练版): 这是一份备战中考初中数学导练学案50讲—第40讲动态问题(讲练版),共43页。学案主要包含了疑难点拨,参考答案等内容,欢迎下载使用。
备战中考初中数学导练学案50讲—第24讲菱形(讲练版): 这是一份备战中考初中数学导练学案50讲—第24讲菱形(讲练版),共33页。学案主要包含了疑难点拨等内容,欢迎下载使用。












