2022广东中考数学模拟卷（三）

这是一份2022广东中考数学模拟卷（三），共17页。试卷主要包含了-13的绝对值是，下列计算正确的是，下列说法正确的是，1,乙组数据的方差s2乙=0，已知P=÷aa2−9等内容，欢迎下载使用。

2022年广东省中考模拟试卷（三）
(本试卷满分120分,考试时间90分钟)
第Ⅰ卷(选择题共30分)
一、 选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.-13的绝对值是 ( )
A.13 B.-13 C.3 D.-3
2.在下列图形中,既是轴对称图形又是中心对称图形的是 ( )

A.直角三角形 B.正五边形 C.正方形 D.平行四边形
3.如图,CD为⊙O的直径,AB为⊙O的弦,且AB=10,若CD⊥AB于点E,则AE的长是 ( )

A.4 B.5 C.6 D.8
4.下列计算正确的是 ( )
A.b3·b3=2b3 B.a-（b+c）=a-b+c
C.（a+b）2=a2+b2 D.（a5）2=a10
5.若点A(x1,y1),B(x2,y2)在反比例函数y=-3x的图象上,且x1<0 A.y1<00>y2
C.y1>y2>0 D.y1 6.下列说法正确的是 ( )
A.为了了解全国中学生的睡眠情况,应该采用普查的方式
B.某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖
C.若甲组数据的方差s2甲=0.1,乙组数据的方差s2乙=0.2,则乙组数据比甲组数据稳定
D.一组数据1,5,3,2,3,4,8的众数和中位数都是3
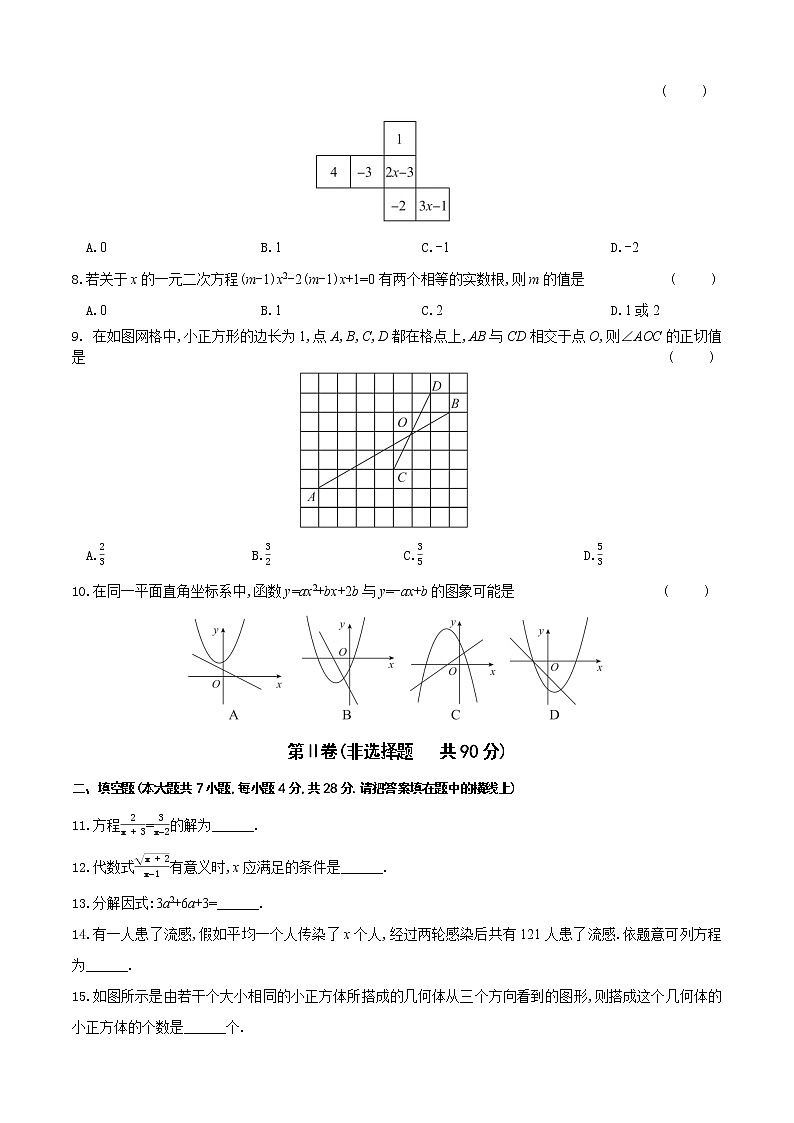
7.如图是一个正方体的平面展开图,若正方体中相对的面上的数字或代数式的乘积都小于0,则整数x的值是
( )

A.0 B.1 C.-1 D.-2
8.若关于x的一元二次方程(m-1)x2-2(m-1)x+1=0有两个相等的实数根,则m的值是 ( )
A.0 B.1 C.2 D.1或2
9. 在如图网格中,小正方形的边长为1,点A,B,C,D都在格点上,AB与CD相交于点O,则∠AOC的正切值是 ( )

A.23 B.32 C.35 D.53
10.在同一平面直角坐标系中,函数y=ax2+bx+2b与y=-ax+b的图象可能是 ( )

第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共7小题,每小题4分,共28分.请把答案填在题中的横线上)
11.方程2x+3=3x−2的解为______.
12.代数式x+2x−1有意义时,x应满足的条件是______.
13.分解因式:3a2+6a+3=______.
14.有一人患了流感,假如平均一个人传染了x个人,经过两轮感染后共有121人患了流感.依题意可列方程为______.
15.如图所示是由若干个大小相同的小正方体所搭成的几何体从三个方向看到的图形,则搭成这个几何体的小正方体的个数是______个.

16.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC的内切圆,OA,OB与⊙O分别交于点D,E.则劣弧的长是______.

17.如图,ABCD是正方形,∠CAB的角平分线交BC于点E,过点C作CF⊥AE交AE的延长线于点G,CF与AB的延长线交于点F,连接BG,DG,DG与AC相交于点H.则下列结论:①△ABE≌△CBF;②GF=CG;③BG⊥DG;④DH=(2-1)AE.其中正确的结论是(填写所有正确答案的序号)______.

三、解答题(本大题共8小题,共62分.解答应写出必要的文字说明、证明过程或演算步骤)
18.已知:如图,E为BC上一点,AC∥BD,AC=BE,BC=BD.
求证:AB=DE.




19.已知P=（a-3+9a+3）÷aa2−9.
(1)化简P;
(2)若a为方程13x2-x-2=0的解,求P的值.






20.某班举行跳绳比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D的四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有______名;
(2)在扇形统计图中,m的值为______,表示D等级的扇形的圆心角为______度;
(3)现决定从本次比赛获得B等级的学生中,选出2名去参加学校的游园活动.已知B等级学生中男生有2名,其他均为女生.请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.





21.疫情期间,为满足口罩需求,某学校决定购进A,B两种型号的口罩.若购进 A型口罩10盒,B型口罩5盒,共需1 000元;若购进A型口罩4盒,B型口罩3盒,共需550元.
(1)求A,B两种型号的口罩每盒各需多少元?
(2)若该学校决定购进这两种型号口罩共计200盒,考虑到实际要求,要求购进A型口罩的盒数不超过B型口罩盒数的6倍.请为该学校设计出最省钱的购买方案,并说明理由.








22.如图所示,一次函数y=k1x+8的图象与坐标轴分别相交于点A,B,与反比例函数y=k2x的图象相交于点C,D.过点C作CE⊥y轴,垂足为E,且CE=2.
(1)求4k1-k2的值;
(2)若CD=2AC,求反比例函数的解析式.








23.如图所示,在△ABC中,AB=AC=23,∠B=30°,点O为边BC上一点,以O为圆心的圆经过点A,B.
(1)求作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)求证:AC是⊙O的切线;
(3)若点P为⊙O上一点,且=,连接PC,求线段PC的长.







24.已知抛物线G:y=x2-2mx与直线l:y=3x+b相交于A,B两点(点A的横坐标小于点B的横坐标).
(1)求抛物线y=x2-2mx顶点的坐标(用含m的式子表示);
(2)已知点C(-2,1),若直线l经过抛物线G的顶点,求△ABC面积的最小值;
(3)若平移直线l,可以使A,B两点都落在x轴的下方,求实数m的取值范围.












25.如图所示,ABCD为平行四边形,AD=13,AB=25,∠DAB=α,且cosα=513,点E为直线CD上一动点,将线段EA绕点E逆时针旋转α得到线段EF,连接CF.
(1)求平行四边形ABCD的面积;
(2)当点C,B,F三点共线时,设EF与AB相交于点G,求线段BG的长;
(3)求线段CF的长度的最小值.



2022年广东省中考模拟试卷（三）

1.A【解析】负数的绝对值等于它的相反数，故－13的绝对值为13，故选A．
2.C【解析】由轴对称图形与中心对称图形的概念可知，选项A的图形既不是轴对称图形，也不是中心对称图形，故选项A错误；选项B的图形是轴对称图形，但不是中心对称图形，故选项B错误；选项C的图形既是轴对称图形又是中心对称图形，故选项C正确；选项D的图形是中心对称图形，但不是轴对称图形，故选项D错误.综上，故选C．
3.B【解析】因为CD⊥AB，所以AE=BE=12AB=5，故选B．
4.D【解析】选项A中，b3·b3=b6，故选项A错误；选项B中，a－(b+c)=a－b－c，故选项B错误；选项C中，(a+b)2=a2+b2+2ab，故选项C错误；选项D中，(a5)2=a10，故选项D正确.综上，故选D．
5.B【解析】因为反比例函数y=－3x的图象分布在第二、四象限，且当x<0时，y>0；当x>0时，y<0，所以当x1<00>y2，故选B．
6.D【解析】对于选项A，为了了解全国中学生的睡眠情况，应该采用随机调查的方式，故选项A错误；对于选项B，某种彩票的中奖机会是1%，则买100张这种彩票不一定会中奖，故选项B错误；对于选项C，方差越小数据越稳定，S2甲=0.1,S2乙=0.2，甲组数据的方差比乙组数据的方差小，所以甲组数据比乙组数据稳定，故选项C错误；对于选项D，将这组数据按从小到大的顺序排列为1，2，3，3，4，5，8，其中3出现的次数最多，故众数是3，排在最中间的数据是3，故中位数是3，故选项D正确，故选D．
7.B【解析】由题知4(2x－3)<0 , －3(3x－1)<0,解得13 8.C【解析】由题知m－1≠0, Δ=4(m－1)2－4(m－1)=0,解得m=2，故选C．
9.A【解析】如图，作BE∥CD，连接AE，则∠AOC=∠ABE.由勾股定理得BE2=32+62=45，AE2=22+42=20，AB2=42+72=65，所以BE2+AE2=AB2，所以由勾股定理逆定理得∠AEB=90°，所以tan∠ABE=AEBE=2045=23，所以tan∠AOC=tan∠ABE=23，故选A．

10.D【解析】对于选项A，一次函数的图象经过第一、二、四象限，则－a＜0，即a＞0，b＞0，所以函数y=ax2+bx+2b的图象开口向上，对称轴x=-b2a＜0，与 y轴的交点位于直线的上方，由ax2+bx+2b=－ax+b整理得ax2+(a+b）x+b=0，由于Δ=(a+b）2－4ab=(a－b）2≥0，则两函数图象有交点，故选项A错误；对于选项B，一次函数的图象经过第二、三、四象限，则－a＜0，即a＞0，b＜0，所以函数y=ax2+bx+2b开口向上，对称轴x=-b2a＞0，故选项B错误；对于选项C，一次函数的图象经过第一、二、三象限，则－a＞0，即a＜0，b＞0，所以函数y=ax2+bx+2b开口向下，对称轴x=-b2a＞0，故选项C错误；对于选项D，一次函数的图象经过第二、三、四象限，则－a＜0，即a＞0，b＜0，所以函数y=ax2+bx+2b开口向上，对称轴x=-b2a>0，且两函数图象有交点,故选项D正确．综上，故选D．
11.x=-13【解析】方程两边同乘(x+3)(x-2),得2(x-2)=3(x+3),解得 x=-13.检验:当x=-13时,(x+3)(x-2)≠0,∴原方程的解为 x=-13.
12.x≥－2且x≠1【解析】由题知x+2≥0,x－1≠0,解得x≥－2且x≠1.
13.3(a+1)2【解析】原式=3(a2+2a+1)=3(a+1)2.
14.(1+x)2=121【解析】由题知，若一个人患流感，则第一轮感染后患流感的总人数为1+x，第二轮感染后患流感的总人数为(1+x)(1+x)，故可列方程为(1+x)2=121.
15.7【解析】在俯视图上标出相应位置摆放小正方体的个数，如图所示，由图知，需要小正方体的个数为7.

16.3π2【解析】∵∠C=90°，AC=8，BC=6，∴AB=10.∵⊙O为△ABC的内切圆，∴OD=6+8－102=2，OA平分∠BAC，OB平分∠ABC，∴∠CAO+∠CBO=12∠C,∴∠AOB=90°+12∠C=90°+12×90°=135°，∴劣弧的长为135π×2180=3π2．
17.①②③【解析】对于①，∵四边形ABCD为正方形，∴AB=CB，∠ABC=∠CBF=90°.∵AG⊥CF，∴∠AGF=90°，∴∠GAF+∠F=90°.∵∠BCF+∠F=90°，∴∠GAF=∠BCF，∴△ABE≌△CBF，故①正确；对于②，∵AG是∠CAB的平分线，∴∠BAG=∠CAG.∵∠AGF=∠AGC=90°，AG=AG，∴△AFG≌△ACG，∴GF=CG，故②正确；对于③，∵∠CBF=90°，GF=CG，∴BG=CG，∴∠CBG=∠BCG.∵∠ABC=∠DCB=90°，∴∠ABG=∠DCG.∵AB=DC，∴△ABG≌△DCG，∴∠AGB=∠DGC.∵∠DGC+∠AGD=∠AGC=90°，∴∠AGB+∠AGD=90°，∴BG⊥DG，故③正确；对于④，∵△ABG≌△DCG，∴∠CDG=∠BAG=∠CAG.∵∠DCH=∠ACE，∴△DCH∽△ACE，∴DHAE=DCAC=22，∴DH=22AE，故④错误．综上，正确的结论是①②③.
18.【解析】∵AC∥BD,
∴∠C=∠EBD.
又∵AC=BE,BC=BD,
∴△ABC≌△EDB(SAS),
∴AB=DE.
19.【解析】(1)P=(a−3)(a+3)+9a+3×(a+3)(a−3)a=a(a-3)=a2-3a,
即P=a2-3a.
(2)∵a为方程13x2-x-2=0的解,
∴13a2-a-2=0,∴a2-3a-6=0,
∴a2-3a=6,
∴P=6.
20.【解析】(1)20.
(2)40,72.
(3)B等级人数为20-3-8-4=5(人),其中2名男生、3名女生，从中选2名的所有可能情况如表所示.

由上述表格可知,总共有20种等可能的情况,其中恰好为一男一女的有12种结果,分别是(男1,女1),(男1,女2),(男1,女3),(女1,男1),(女1,男2),(女2,男1),(女2,男2),(女3,男1),(女3,男2),(男2,女1),(男2,女2),(男2,女3),
∴P（所选2名学生恰好是一名男生和一名女生）=1220=35.
21.【解析】(1)设A型口罩每盒a元,B型口罩每盒b元,
则10a+5b=1 000,4a+3b=550, 解得a=25,b=150,
答:A型口罩每盒25元,B型口罩每盒150元.
(2)设A型口罩购买m盒,则B型口罩购买(200-m)盒,此时总费用为y元,
则有y=25m+150(200-m),
化简得y=30 000-125m.
∵m≤6(200-m),
∴m≤17137.
又∵m为整数,∴m≤171.
在y=30 000-125m中,-125<0,
∴y随x的增大而减小.
又∵m≤171,
∴当m=171时,总费用y有最小值,
此时200-m=29.
答:购买A型口罩171盒,B型口罩29盒时最省钱.
22.【解析】(1)设点C(xc，yc）.
∵CE=2,∴xC=-2.
∵点C为直线y=k1x+8和双曲线y=k2x的交点,
∴yC=-2k1+8=k2−2,化简得4k1-k2=16.
(2)如图所示,过点D作DG⊥y轴于点G.

∵CE∥DG,
∴△ACE∽△ADG,
∴CEDG=ACAD.
∵CD=2AC,则AD=3AC,
∴DG=3CE=6.
∵点D在反比例函数y=k2x的图象上,
∴点D（-6,-k26）.
又∵点D（-6,-k26）在直线y=k1x+8上,
∴-k26=-6k1+8.①
又∵4k1-k2=16,②
联立方程①②解得k1=1,k2=-12,
∴反比例函数解析式为y=-12x.
23.【解析】(1)如图所示.

(2)证明:如图所示,连接OA.
∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=120°.
又∵OA=OB,
∴∠BAO=∠B=30°,
∴∠OAC=∠BAC-∠BAO=120°-30°=90°,
即OA⊥AC,
∴AC为⊙O的切线.
(3)①当点P在AB下方P1处时,如图所示,连接CP1.
∵=,
∴∠P1OB=∠P1OA=120°.
又∵∠AOC=60°,
∴∠COP1=60°,
∴△AOC≌△P1OC,
∴P1C=AC=23;
②当点P在AB上方P2处时,
如图所示,连接CP2,过点P2作P2H⊥BC于点H.
∵=,
∴∠AOP2=∠BOP2=60°.
∵AB=AC=23,OA⊥AC,∠ACB=30°,
∴在Rt△OAC中,OC=ACcos30°=4,OA=2,
∴OA=OB=OP2=2,BC=6.
又∵∠BOP2=60°,
∴在Rt△P2HO中,HO=OP2·cos60°=1,
P2H=OP2·sin60°=3,
∴HC=HO+OC=5,
∴在 Rt△P2HC 中,P2C=P2H2+HC2=3+25=27.
综上所述,PC=23或27.
24.【解析】(1)∵y=x2-2mx=(x-m)2-m2,
∴抛物线的顶点坐标是(m,-m2).
(2)∵直线l:y=3x+b经过抛物线G的顶点(m,-m2),
∴-m2=3m+b,则b=-m2-3m,
∴直线l:y=3x-m2-3m.
联立y=x2−2mx, y=3x−m2−3m,
消去y可得x2-(2m+3)x+m(m+3)=0,
即(x-m)［x-(m+3)］=0，
解得x=m或x=m+3.
∵点A的横坐标小于点B的横坐标,
∴xA=m,xB=m+3.
过点C作x轴的垂线交直线AB于点H ,如图1,

则S△ABC=12CH×｜xB-xA｜.
∵点C(-2,1),H(-2,-6-m2-3m),
∴CH=｜yC-yH｜=m2+3m+7,
∴S△ABC=32(m2+3m+7)=32（m+32）2+194,
∴当m=-32时,△ABC的面积有最小值578.
(3)由题可知抛物线G与x轴交于O(0,0),D(2m,0)两点.
①当m<0时,函数图象如图2所示.

由图可知,平移直线l时,若要求A,B两点都能够落在x轴下方,
只需要当l经过坐标原点O时,与抛物线的另一个交点E在x轴的下方,
此时直线l的解析式为y=3x.
令x2-2mx=3x,
解得x=0或x=2m+3,
当x=2m+3时,y=3x=3(2m+3)=6m+9,
即点E(2m+3,6m+9),
由6m+9<0,解得m<-32;
②当m=0时,抛物线为y=x2,平移直线l时,交点A,B不可能位于x轴下方;

③当m>0时,函数图象如图3所示.
由图可知,平移直线l时,若要求A,B两点都能够落在x轴下方,只需要当直线l经过点D时,与抛物线的另一个交点E在x轴的下方,
此时直线l的解析式为y=3(x-2m).
令x2-2mx=3(x-2m),
解得x=3或x=2m.
当x=3时,y=3(x-2m)=3(3-2m)=9-6m,
即点E(3,9-6m),
由9-6m<0,解得m>32.
综上所述,当m<-32或m>32时,平移直线l,可以使A,B两点都落在x轴的下方.
25.【解析】(1)如图1所示,过点A作AK⊥CD交CD的延长线于点K.
∵AB∥CD,
∴∠ADK=∠DAB=α.
∵cos∠DAB=513,AD=13,
∴DK=AD·cos∠ADK=5,
∴AK=AD2−DK2=12,
∴平行四边形ABCD的面积为AB×AK=25×12=300.

(2)当C,B,F三点共线时,如图1所示,延长CD到点P使得AP=AD,
∴∠ADP=∠P.
∵∠DAB=α,DC∥AB,
∴∠ADP=∠DAB=α,∴∠P=α.
又∵∠AEF=∠C=α,
∴∠PEA+∠CEF=180°-α,
∠EFC+∠CEF=180°-α,
∴∠PEA=∠EFC.
∵EA=EF,∠P=∠C=α,
∴△PEA≌△CFE,
∴CE=AP=13,PE=CF,
∴DE=CD-CE=25-13=12.
由(1)得AK=12,
∴在Rt△AKD中,DK=5,
∴PD=10,
∴PE=PD+DE=10+12=22=CF,
∴BF=CF-CB=22-13=9.
∵BG∥CE,∴△GBF∽△ECF,
∴BFCF=BGCE,
∴922=BG13,
∴BG=11722.
(3)如图2所示,作点A关于直线CD的对称点A′,连接EA′,AA′,A′F,以E为圆心,EA为半径作圆.

∵EA=EA′=EF,
∴点A,A′,F在⊙E上.
∵∠AEF=α,
∴∠AA′F=α2,
∴点F在与直线AA′夹角为α2且经过点A′的直线上运动.
设直线A′F与CD交于点Q,直线AA′与直线CD交于点M,直线A′F与直线CB交于点R,过点C作CH⊥A′F于点H,当点F与点H重合时,CF取得最小值.
易得Rt△A′MQ∽Rt△CHQ,
∴∠QCH=∠MA′Q=α2.
又∵∠DCB=α,
∴∠BCH=∠QCH=α2,
∴△QCR为等腰三角形,
∴CQ=CR.
由(2)得CR=22,MD=5,
∴CQ=22.
又∵CM=CD+DM=25+5=30,
∴MQ=CM-CQ=30-22=8,
∴在Rt△A′MQ中,A′Q=A′M2+MQ2=122+82=413.
∵Rt△A′MQ∽Rt△CHQ,
∴A′QCQ=A′MCH,
∴41322=12CH,
∴CH=661313,
即CF的长度的最小值是661313.