2020-2021学年第九章 图形的相似综合与测试复习课件ppt

这是一份2020-2021学年第九章 图形的相似综合与测试复习课件ppt，共12页。PPT课件主要包含了学习目标，活动探究一，活动探究二，挑战自我，畅谈收获，我学会了什么，我最感兴趣的是，我能解决等内容，欢迎下载使用。

1、能熟练应用等腰三角形的性质与判定；2、通过独立解决变化中的三角形问题，能够用运动变化的观点研究图形的变化规律，提高分析解决综合问题的能力；3、在探究过程中养成合作和交流意识，渗透“分类讨论”、“数形结合”的思想，积累基本数学活动体验。
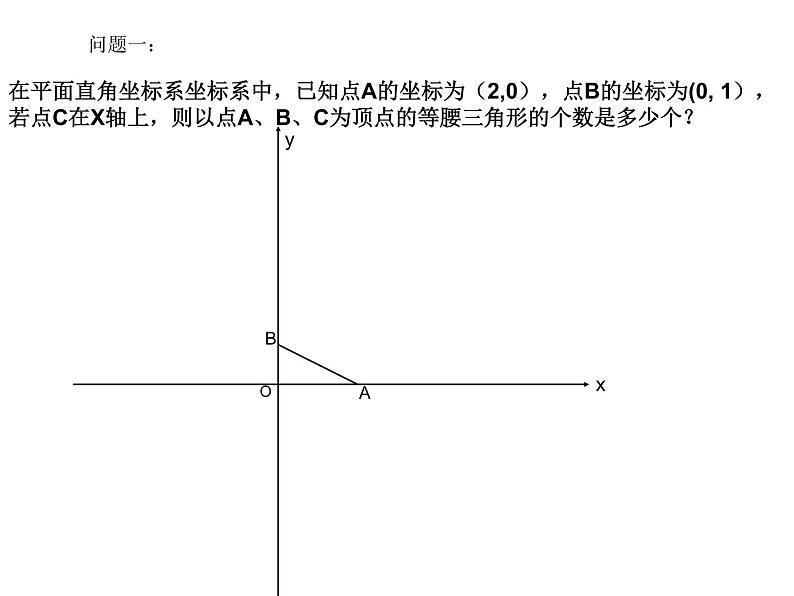
在平面直角坐标系坐标系中，已知点A的坐标为（2,0），点B的坐标为(0, 1），若点C在X轴上，则以点A、B、C为顶点的等腰三角形的个数是多少个？
当给出一条线段作为等腰三角形的一边时，我们要分类讨论
这条线段可能为底边，也可能为腰，当线段为腰时，线段的两端分别可以作为等腰三角形的顶点，共三种情况！
可以借助圆规利用圆的定义，找出三种情况的所有点
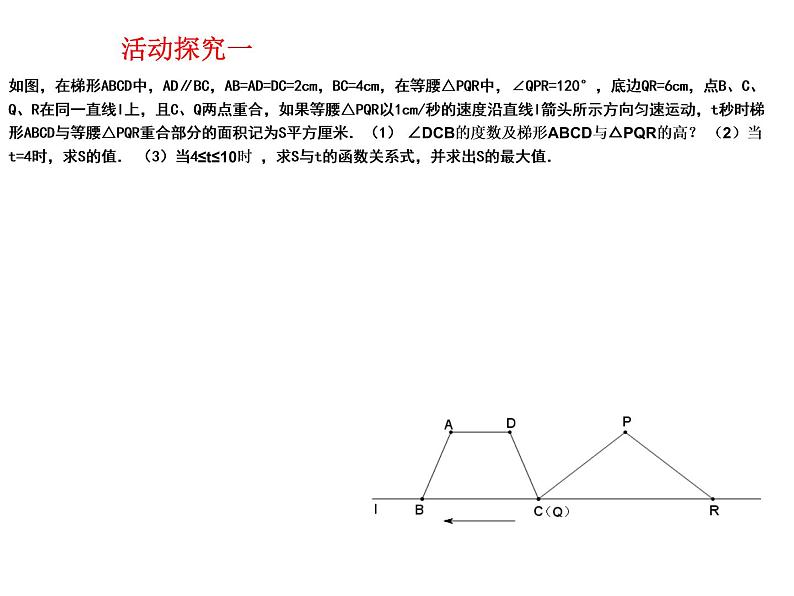
如图，在梯形ABCD中，AD∥BC，AB=AD=DC=2cm，BC=4cm，在等腰△PQR中，∠QPR=120°，底边QR=6cm，点B、C、 Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米．（1） ∠DCB的度数及梯形ABCD与△PQR的高？ （2）当t=4时，求S的值． （3）当4≤t≤10时 ，求S与t的函数关系式，并求出S的最大值．
解决动态问题时：首先需要把动态问题静态化，找准界点，化为几个静态的过程
“以静制动”，抓住变化中的“不变量”，以不变应万变
如图，有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板PHF的直角顶点P落在AD边上（不A、D重合），在AD上适当移动三角板顶点P（1）当三角板两边通过B与C时，求出AP的长？
（2）再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH始终通过点B，另一直角边PF与DC延长线交于点Q，与BC交于点E，能否使CQ=3cm？若能，请你求出这时AP的长；若不能，请你说明理由。
在几何图形中，求线段的问题，往往可以优先考虑三角形相似的问题
利用解方程来解决几何问题，是我们常用的数形结合的思想方法
在这样的综合题中，图形虽然变化了，但是往往解题的思路与方法并没有变化
如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是多少？
当遇到不太容易解决的问题时，可以将图形进行旋转，方向的变化有利于我们发现基本结合图形
我获得的数学方法是……