天津2022年中考数学模拟卷 含答案

天津2022届中考数学模拟卷

【满分：120】

一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.计算的结果是(   )

A.-18 B.2 C.18 D.-2

2.已知为锐角，且，则(   )

A.30° B.45° C.60° D.90°

3.一个由圆柱和长方体组成的几何体如图水平放置，它的俯视图是(   )

A.  B.

C.  D.

4.研究发现，银原子的半径约是0.00015微米，把0.00015用科学记数法表示应是(   )

A. B. C. D.

5.下列各数中，介于5和6之间的数是(   )

A. B. C. D.

6.下列运算中，结果正确的是(   )

A.  B.

C.  D.

7.方程组的解为(   )

A. B. C. D.

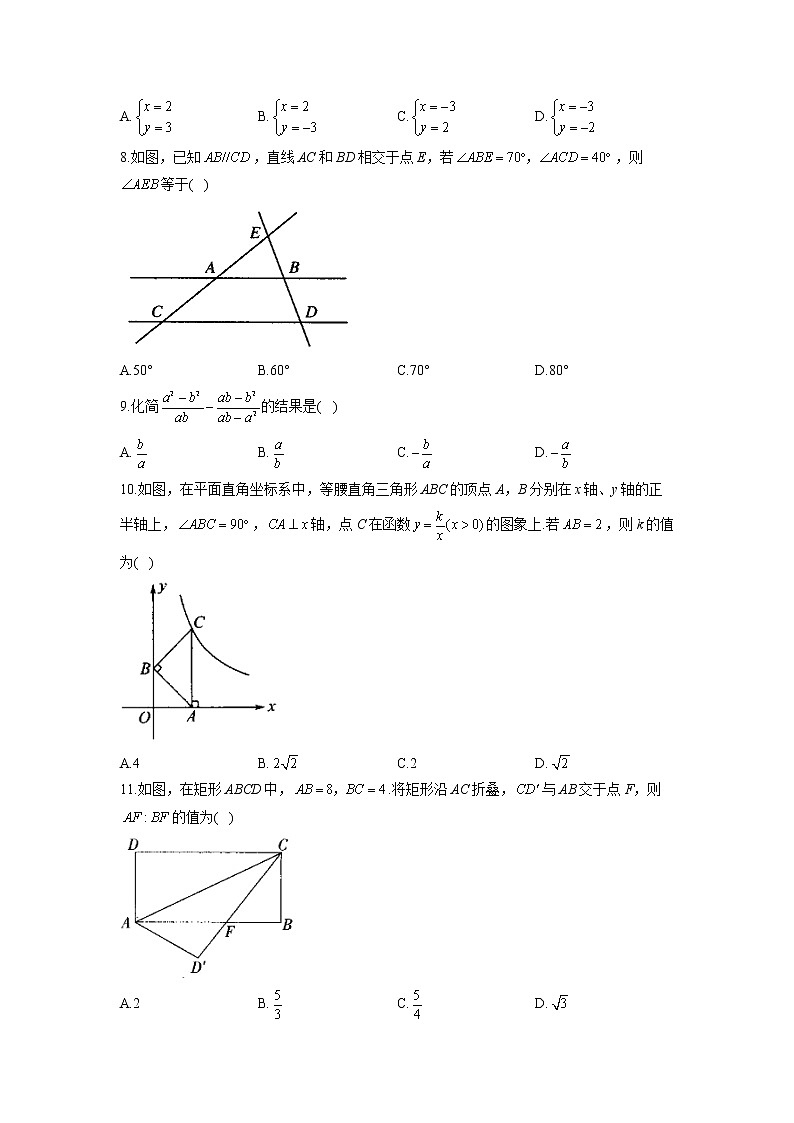
8.如图，已知，直线AC和BD相交于点E，若，则等于(   )

A.50° B.60° C.70° D.80°

9.化简的结果是(   )

A. B. C. D.

10.如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A，B分别在x轴、y轴的正半轴上，，轴，点C在函数的图象上.若，则k的值为(   )

A.4 B. C.2 D.

11.如图，在矩形ABCD中，.将矩形沿AC折叠，与AB交于点F，则的值为(   )

A.2 B. C. D.

12.二次函数的图像如图所示，它的对称轴为直线，与x轴交点的横坐标分别为，，且.下列结论中：①；②；③；④方程有两个相等的实数根；⑤.其中正确的有(   )

A.②③⑤ B.②⑤ C.②④ D.①④⑤

二、填空题（本大题共6小题，每小题3分，共18分）

13.计算的结果是_______________.

14.若,则_______.

15.某校开展以“我和我的祖国”为主题的“大合唱”活动，七年级准备从小明、小东、小聪三名男生和小红、小慧两名女生中各随机选出名男生和一名女生担任领唱，则小聪和小慧被同时选中的概率是___________.

16.关于x的一次函数的图像与直线平行，且过点，则的值是______.

17.如图，正方形ABCD和正方形EFCG的边长分别为3和1，点F，G分别在边BC，CD上，P为AE的中点，连接PG，则PG的长为_____________.

18.对于同一个正六边形花坛，甲、乙两工程师分别构建了如图（1）（2）所示的平面直角坐标系，且两个坐标系的单位长度一致，则在甲所建的坐标系中正六边形的中心G的坐标为______，在乙所建的坐标系中正六边形的中心G的坐标为______.

三、解答题（本大题共7小题，共66分.解答应写出文字说明、演算步骤或推理过程）

19.（8分）解不等式组：，并把解集在数轴上表示出来.

20.（8分）某校九年级共有400名学生，该校对九年级所有学生进行了一次体育测试，并随机抽取甲、乙两个班各50名学生的测试成绩（成绩均为整数，满分50分）进行整理、描述和分析.

下面给出了部分信息.

a.甲班成绩扇形统计图和乙班成绩频数分布直方图如图所示（用x表示成绩，数据分成5组：A.， B.，C.，D.，E. ）.

b.甲、乙两班成绩统计表如下.

c.乙班成绩在D组的具体分数是:

42,42,42,42,42,42,42,42,42,42,43,44,45,45

根据以上信息，回答下列问题：

（1）根据统计图，对比两个班成绩在的学生人数所占的百分比，甲班比乙班__________（填“大“小”“一样”）；

（2）直接写出m,n的值，___________, ___________；

（3）小明这次测试成绩是43分，在班上排名属中游略偏上，小明是甲、乙哪个班级的学生？说明理由；

（4）若成绩达到45分及以上为优秀，估计该校本次测试成绩优秀的学生人数.

21.（10分）某校为检测师生体温，在校门安装了某型号测温门.如图为该测温门截面示意图，已知测温门AD的顶部A处距地面高为2.2 m，为了解自己的有效测温区间，身高1.6 m的小聪做了如下实验：当他在地面N处时测温门开始显示额头温度，此时在额头B处测得A的仰角为18°；在地面M处时，测温门停止显示额头温度，此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度（额头到地面的距离以身高计，计算精确到0.1 m，，，）.

22.（10分）在学习函数时，我们经历了“确定函数的表达式—利用函数图象研究其性质—运用函数解决问题”的学习过程.在画函数图象时，我们通过列表、描点、连线的方法画出了所学的函数图象.同时，我们也学习过绝对值的意义.结合上面经历的学习过程，现在来解决下面的问题：

在函数中，当时，；当时，.

(1)求这个函数的表达式.

(2)在给出的平面直角坐标系中，请直接画出此函数的图象并写出这个函数的两条性质；

(3)函数的图象如图所示，结合你所画的函数图象，直接写出不等式的解集.

23.（10分）如图，PA为的切线，A为切点，点B在上，且，连接AO并延长交PB的延长线于点C，交于点D.

(1)求证：PB为的切线；

(2)连接OB，DP交于点E.若，，求的值.

24.（10分）众志成城抗疫情，全国人民在行动.某公司决定安排大、小货车共20辆，运送260吨物资到A地和B地，支援当地抗击疫情.每辆大货车装15吨物资，每辆小货车装10吨物资，这20辆货车恰好装完这批物资.已知这两种货车的运费如下表：

现安排上述装好物资的20辆货车（每辆大货车装15吨物资，每辆小货车装10吨物资）中的10辆前往A地，其余前往B地，设前往A地的大货车有x辆，这20辆货车的总运费为y元.

（1）这20辆货车中，大货车、小货车各有多少辆？

（2）求y与x的函数解析式，并直接写出x的取值范围；

（3）若运往A地的物资不少于140吨，求总运费y的最小值.

25.（10分）如图,在平面直角坐标系中,已知抛物线的解析式为,正方形OABC的边OA,OC在坐标轴上,且点B的坐标为(2,2).

(1)求抛物线的顶点坐标(用含b的代数式表示),并求出当其顶点在线段BC上时b的值.

(2)在抛物线与x轴所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,请直接写出当时“美点”的个数.

(3)设抛物线的顶点为点D.

①连接BD,CD,当时,求点D的坐标;

②作直线AC,当抛物线的顶点D位于直线AC的下方时,求当点D到直线AC的距离最大时点D的坐标.

答案解析

1.答案：C

解析：.故选C.

2.答案：A

解析：，故选A.

3.答案：C

解析：几何体的俯视图是C项中的图形，故选C.

4.答案：A

解析：，故选A.

5.答案：D

解析：，，

，故选D.

6.答案：D

解析：，故A选项错误；，故B选项错误；，故C选项错误；，故D选项正确.故选D.

7.答案：B

解析：

，得，

解得，把代入①，得，解得，

故方程组的解为故选B.

8.答案：C

解析：，

.

在中，，，

.

9.答案：B

解析：原式.

10.答案：A

解析：在中，，，，

，.

轴，，

，

是等腰直角三角形.

又，

由勾股定理，得.

点C的坐标为.

把点代入函数，得.

故选A.

11.答案：B

解析：设，由折叠的性质知，四边形ABCD是矩形，，

，

，

在中，，

，

，

的值为，故选B.

12.答案：B

解析：观察抛物线可知①，，，，故①错误；②对称轴为直线，与x轴交点的横坐标分别为，，且，，故②正确；③当时，，即，故③错误；④抛物线与直线有两个交点，方程有两个不相等的实数根，故④错误；⑤对称轴为直线，即，，当时，，且，即，，解得，故⑤正确.所以②⑤正确.

13.答案：

解析：.

14.答案：13

解析：.

15.答案：

解析：画树状图如下：

由树状图可知，共有6种等可能的结果，其中小聪和小慧同时被选中的情况有1种，小聪和小慧被同时选中的概率是.故答案为.

16.答案：5

解析：关于x的一次函数的图像与直线平行，

.一次函数的图像过点，，解得，

.

17.答案：

解析：如图，连接CE，过点G作于点H.易知点A，E，C在同一条直线上，是直角三角形.由勾股定理可得，，，.是等腰直角三角形，GH是斜边上的高线，，，.

18.答案：

解析：根据题图（1）中点的坐标，可知甲工程师建立的平面直角坐标系如图所示，连接.易知点G为线段的中点，故点G的坐标为，即.过点C作轴于点M，，即该正六边形的边长为2.在题图（2）中，连接，易知点G为的中点，平分，，又，∴点G的坐标为.

19.答案：

解不等式①，得，

解不等式②，得，

所以不等式组的解集是，

不等式组的解集在数轴上表示如图所示.

20.答案：（1）大

解法提示：甲班成绩在的学生人数所占的百分比为，

乙班成绩在的学生人数所占的百分比为，

故甲班比乙班大.

（2）45；42

解法提示：将乙班成绩按照从小到大的顺序排列，易知第25,26个数据都是42分，故.

由甲班成绩扇形统计图易知，甲班成绩在A组、B组、C组、D组、E组的人数分别为2,2,10,24,12.因为甲班成绩的中位数是44.5分，成绩是整数,所以将甲班成绩按照从小到大的顺序排列后，第25,26个数据分别是44分，45分，所以甲班成绩为45分的学生人数为，故甲班成绩的众数是45分，即.

（3）小明是乙班的学生.

理由：∵小明的成绩为43分，且在班上排名属中游略偏上，

∴小明所在班级成绩的中位数小于43分，

∴小明是乙班的学生.

（4）（人），

即估计该校本次测试成绩优秀的学生人数为188人.

21.答案：小聪在地面的有效测温区间MN的长度约为1.5 m

解析：如图，延长BC交AD于E.

由题意得四边形DEBN、四边形MCBN都为矩形，

，，，.

，

.

，

.

，

.

.

.

答：小聪在地面的有效测温区间MN的长度约为1.5 m.

22.答案：（1）把分别代入表达式，得，把分别代入表达式 ，得，解得，所以函数表达式为：.

如图所示：

函数性质举例：①函数图象关于直线对称（或函数图象是个轴对称图形）；

②函数的最小值是-3；

③当时，y随x的增大而减小，当时，y随x的增大而增大；

（写对两个即可）

（3）或.

23.答案：(1)见解析

(2)

解析：(1)如图，连接OB，OP.

为的切线，，.

在与中，

，，

.

是的半径，是的切线.

(2)如图，连接BD，AB交OP于点G.设.在中，，，，，.

，PB是的切线，，，，.

设.在中，，

，，.

在中，，

，.

在中，.

，，，

，，.

24.答案：（1）这20辆货车中，大货车有12辆，小货车有8辆.

（2）y与x的函数解析式为，x的取值范围为且x是正整数.

（3）若运往A地的物资不少于140吨，总运费y的最小值为16400元.

解析：（1）设大货车有a辆，小货车有b辆，

根据题意得解得.

答：这20辆货车中，大货车有12辆，小货车有8辆.

（2）因前往A地货车共10辆，其中大货车x辆，则前往A地小货车有辆，

前往B地大货车有辆，前往B地小货车有辆，

根据题意得，

化简得

x的取值范围为，且x是正整数.

答：y与x的函数解析式为，

x的取值范围为且x是正整数.

（3）根据题意得，解得.

由（2）知.

.

又，

y随x的增大而增大.

当时，y最小，且.

答：若运往A地的物资不少于140吨，总运费y的最小值为16400元.

25.答案：(1),

抛物线的顶点坐标为.

当顶点在线段BC上时,

易知,

.

(2)当时,“美点”的个数为4 040.

解法提示:,

抛物线.

令,

解得,

故该抛物线与x轴有两个交点,交点坐标分别为.

易知抛物线与x轴所围成的封闭图形的边界上,位于x轴上的“美点”的个数为2 021,位于抛物线上的“美点”的个数为2 019(除点和),

故当时,“美点”的个数为4 040.

(3)①,点D的坐标为,

,

整理,得,

解得或0.

故点D的坐标为或.

②,

点D在抛物线上.

方法一:如图,设抛物线与直线AC交于点H,K,点E为线段压上一点(不与点H,K重合),

过点E作轴交抛物线于点F.

由,

易得直线AC的解析式为.

设点F的横坐标为a,则,

.

设点F到直线AC的距离为h,则,

故当EF最大,且点D与点F重合时,点D到直线AC的距离最大.

,

当EF最大时,,

此时,

当点D到直线AC的距离最大时,点D的坐标为.

方法二:过直线AC下方抛物线上的一点,作直线AC的平行线l,当直线l与抛物线有且只有一个交点时,该交点到直线AC的距离最大,即当点D与该交点重合时,点D到直线AC的距离最大.

易求直线AC的解析式为,

故设直线l的解析式为,

令,整理得.

当此方程有两个相等的实数根时,

,解得,代入,解得,

故当点D到直线AC的距离最大时点D的坐标为.