

初中第三章 投影与三视图综合与测试单元测试课时作业
展开第三次质量评估试卷
[考查范围:上册+下册第1~3章]
一、选择题(每小题3分,共30分)
1.下列说法正确的是( C )
A.物体在阳光下的投影只与物体的高度有关
B.小明的个子比小亮高,因此无论在什么情况下,小明的影子一定比小亮的影子长
C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化
D.物体在阳光照射下,影子的长度和方向都是固定不变的
2.晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影是( D )
A.变长 B.变短 C.先变长后变短 D.先变短后变长
3.下面四个立体图形中,主视图是三角形的是( C )
A. B. C. D.
4.下列说法中正确的是( D )
A.任意两个矩形都相似 B.任意两个菱形都相似
C.相似图形一定是位似图形 D.位似图形一定是相似图形
5.在△ABC中,∠C=90°,AC=1,BC=2,则 cos A的值是( B )
A. B. C. D.
第6题图
6.如图所示,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=5 m,则点P到CD的距离是3 m,则点P到AB的距离是( C )
A. m B. m C. m D. m
7.已知在△ABC中,∠C=Rt∠,AC=3,BC=4,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙O内,点B在⊙C外,则半径r的取值范围是( D )
A.<r<4 B.<r<3 C.r>3 D.3<r<4
第8题图
8.如图所示,圆锥的表面展开图由一扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,则这个扇形的面积为( C )
A.100π B.200π C.300π D.400π
9.若二次函数y=x2+(m+1)x-m的图象与坐标轴只有两个交点,则满足条件的m的值有( C )
A.1个 B.2个 C.3个 D.4个
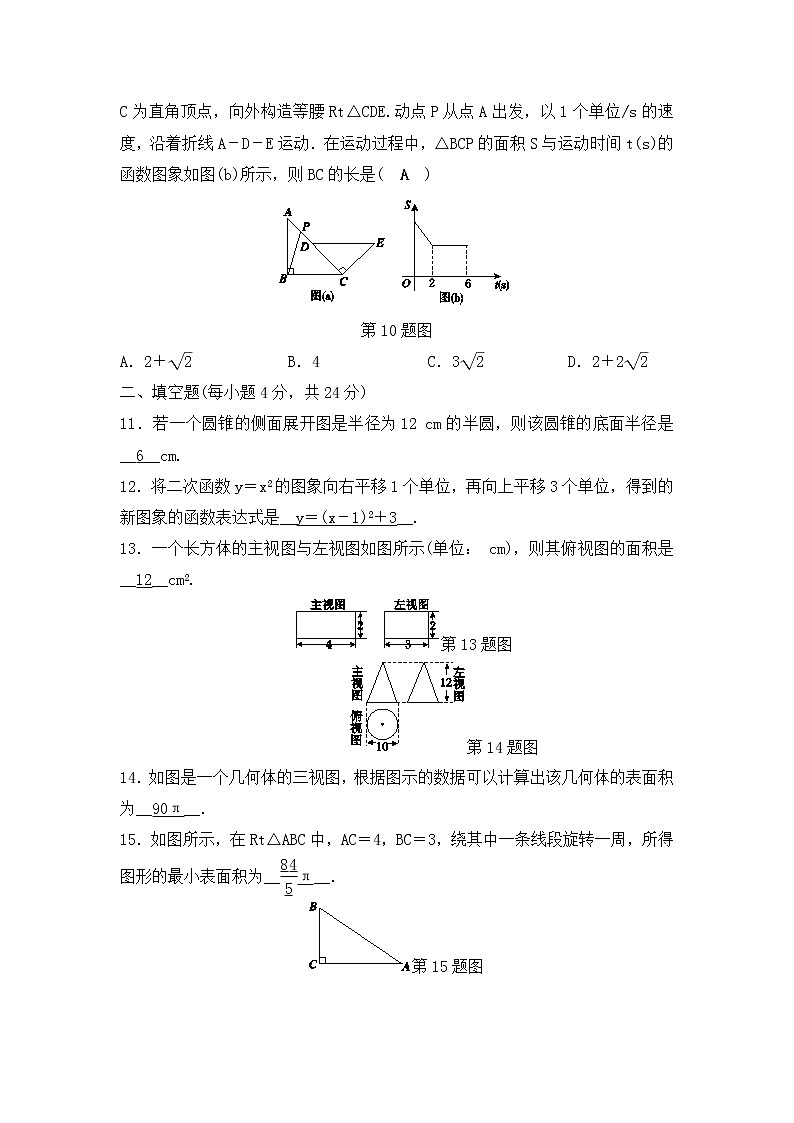
10.如图所示,在等腰Rt△ABC中,D为斜边AC边上一点,以CD为直角边、点C为直角顶点,向外构造等腰Rt△CDE.动点P从点A出发,以1个单位/s的速度,沿着折线A-D-E运动.在运动过程中,△BCP的面积S与运动时间t(s)的函数图象如图(b)所示,则BC的长是( A )
第10题图
A.2+ B.4 C.3 D.2+2
二、填空题(每小题4分,共24分)
11.若一个圆锥的侧面展开图是半径为12 cm的半圆,则该圆锥的底面半径是__6__cm.
12.将二次函数y=x2的图象向右平移1个单位,再向上平移3个单位,得到的新图象的函数表达式是__y=(x-1)2+3__.
13.一个长方体的主视图与左视图如图所示(单位: cm),则其俯视图的面积是__12__cm2.
第13题图
第14题图
14.如图是一个几何体的三视图,根据图示的数据可以计算出该几何体的表面积为__90π__.
15.如图所示,在Rt△ABC中,AC=4,BC=3,绕其中一条线段旋转一周,所得图形的最小表面积为__π__.
第15题图
第16题图
16.如图所示,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A′时,竹竿的另一端B向右滑到了点B′,此时倾斜角为β.
(1)线段AA′的长为__a(sin_α-sin_β)__;
(2)当竹竿AB滑到A′B′位置时,AB的中点P滑到了P′位置,则点P所经过的路线长为____.(两小题均用含a,α,β的代数式表示)
三、解答题(共66分)
第17题图
17.(6分)指出图中的图形分别能折成什么几何体.
解:图(1)沿虚线折叠后得到四棱锥.
图(2)以小圆作底,将扇形两半径叠合会得到一个圆锥.
图(3)以两个正六边形为底,长方形沿虚线依次折叠,使宽叠合围成一个六棱柱.
第18题图
18.(8分)如图所示,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影EF.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4.2 m,请你计算DE的长.
第18题答图
解:(1)连结AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AB=5 m,某一时刻AB,DE在阳光下的投影BC=3 m,EF=4.2 m,
∴=,则=,解得DE=7.
即DE的长为7 m.
第19题图
19. (8分)如图所示,抛物线y=-x2+2x+3与y轴交于点C,顶点为D.
(1)求顶点D的坐标;
(2)求△OCD的面积.
解:(1)y=-x2+2x+3=-(x-1)2+4,
即顶点D的坐标为(1,4).
(2)把x=0代入y=-x2+2x+3,得y=3,
即OC=3,
S△OCD=×3×1=.
第20题图
20.(8分)某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图如图所示,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
解:由三视图可知:茶叶罐的形状为圆柱体,且茶叶罐的底面半径R为50毫米,高h为150毫米,
∵每个密封罐所需钢板的面积即为圆柱体的表面积,
∴S表面积=2πR2+2πRh
=2π×502+2π×50×150
=20000π(平方毫米).
即制作每个密封罐所需钢板的面积为20000π平方毫米.
21.(8分)图(a)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(b)所示.
(1)请画出这个几何体的俯视图;
(2)图(c)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6 m,圆柱部分的高OO1=4 m,底面圆的直径BC=8 m,求∠EAO的度数.(结果精确到0.1°)
第21题图
解:(1)画出俯视图,如图(a)所示.
第21题答图(a)
第21题答图(b)
(2)如图(b),连结EO1,则EO1经过点O,
∵EO1=6 m,OO1=4 m,
∴EO=EO1-OO1=6-4=2 m,
∵AD=BC=8 m,
∴OA=OD=4 m,
在Rt△AOE中,tan∠EAO===,
∴∠EAO≈26.6°.
第22题图
22.(8分)一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,已知木箱高PQ=h,斜面坡角α满足tan α=(α为锐角),求木箱顶端P离地面AB的距离PC.
解:由题意,得∠DPQ=α,
∴tan∠DPQ=,即=,∴DQ=h,
∴PD== h,AD=m-h,
∵△ACD∽△PQD,
∴=,即=,解得CD=m-h,∴PC=CD+PD=m+h.
23.(10分)某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2-2kn+9(k+3)(k为常数),且得到了表中的数据.
月份n(月) | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)求y与x满足的关系式,并说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.
解:(1)由题意,设y=a+,
由表中数据可得解得∴y=6+,
由题意,若12=18-,则=0,∵x>0,∴>0,
∴不可能.
(2)将n=1,x=120代入x=2n2-2kn+9(k+3),得:120=2-2k+9k+27,
解得k=13,∴x=2n2-26n+144,
将n=2,x=100代入x=2n2-26n+144也符合,
∴k=13,
由题意,得18=6+,解得x=50,
∴50=2n2-26n+144,即n2-13n+47=0,
∵Δ=(-13)2-4×1×47<0,
∴方程无实数根,∴不存在.
(3)第m个月的利润为W,
W=x(18-y)=18x-x=12(x-50)
=24(m2-13m+47),
∴第(m+1)个月的利润为W′=24[(m+1)2-13(m+1)+47]=24(m2-11m+35),
若W≥W′,W-W′=48(6-m),m取最小1,W-W′取得最大值240;
若W<W′,W′-W=48(m-6),由m+1≤12知m取最大11,W′-W取得最大值240;
∴m=1或11.
24.(10分)如果正方形网格中的每一个小正方形边长都是1,则每个小格的顶点叫做格点.
(1)在图(a)中以格点为顶点画一个三角形,使三角形的三边长分别为3,,2.
(2)在图(b)中以格点为顶点画一个面积为10的正方形.
(3)观察图(c)中带阴影的图形,请你将它适当剪开,重新拼成一个正方形[要求:在图(c)中用虚线作出,并用文字说明剪拼方法];图c说明:______________.
(4)观察图(d)中的立方体,沿着一些棱将它剪开,展开成平面图形.若正方体的表面积为12,请你在图中以格点为顶点画出一个立方体的平面展开图.(只需画出一种情形)
图(a) 图(b) 图(c) 图(d)
第24题图
解:(1)如图(a)所示,△ABC即为所求的三角形.
图(a) 图(b) 图(c) 图(d)
第24题答图
(2)如图(b)所示,正方形ABCD的面积为10.
(3)如图(c)所示,说明沿虚线剪开,然后①,②,③分别对应拼接即可.
(4)∵立方体有6个表面,∴每一个面的面积为12÷6=2,
所以如图(d)所示.答案不唯一.
浙教版九年级下册第三章 投影与三视图综合与测试单元测试课堂检测: 这是一份浙教版九年级下册第三章 投影与三视图综合与测试单元测试课堂检测,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙教版九年级下册第二章 直线与圆的位置关系综合与测试单元测试达标测试: 这是一份浙教版九年级下册第二章 直线与圆的位置关系综合与测试单元测试达标测试,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中第三章 投影与三视图综合与测试单元测试课后复习题: 这是一份初中第三章 投影与三视图综合与测试单元测试课后复习题,共10页。













