2020-2021学年吉林省四平市某校初三（下）5月月考数学试卷 含解析

这是一份2020-2021学年吉林省四平市某校初三（下）5月月考数学试卷 含解析，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 如图，给出了吉林市2021年4月13日的最高气温和最低气温，则这天的温差是( )

A.−4∘CB.4∘C C.8∘CD.12∘C

2. 《中国5G经济报告2020》预计到2025年，中国5G用户将达到816000000，数据816000000用科学记数法表示为( )
×107×108×109×1010

3. 三星堆考古成果是中华文明多元一体发展模式的重要实物例证．下列出土文物从图案看不是轴对称图形的是( )
A.B.
C.D.

4. 如图，一个倾斜的天平两边分别放有小立方体和砝码，每个砝码的质量都是5g，每个小立方体的质量都是m(g)，则m的取值范围为( )

A.m>15B.m<15C.m>152D.m<152

5. 如图，建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，其数学道理是( )

A.两点确定一条直线
B.两点之间，线段最短
C.垂线段最短
D.平行于同一条直线的两条直线平行

6. 如图，直线a//b，点A在直线b上，以点A为圆心，2cm长度为半径画弧，分别交直线a，b于C，B两点，连接AC，BC．若∠1=60∘，则△ABC的周长为( )

A.3cmB.2cmC.23cmD.6cm
二、填空题

计算： 9−2=________.

一本笔记本的原价是n元，现在按8折出售，购买5本笔记本需要付费________元．

若分式1x−1 的值等于−3，则x=________.

若关于x的一元二次方程x2=c−1有实数根，则c的值可以为________（写出一个即可）．

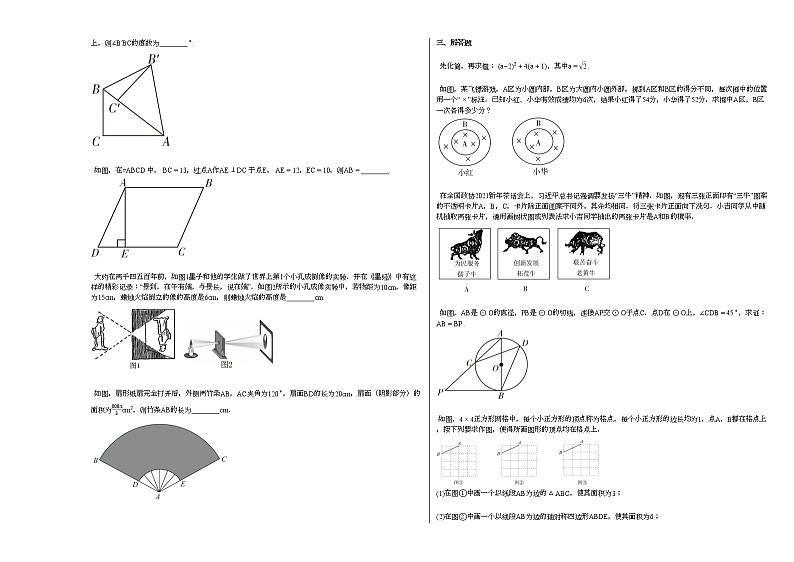
如图，在Rt△ABC中， ∠C=90∘ ，∠BAC=40∘，将Rt△ABC绕点A旋转得到Rt△AB′C′，且点C′落在AB上，则∠B′BC的度数为________​∘.


如图，在▱ABCD 中， BC=13，过点A作AE⊥DC 于点E， AE=12，EC=10，则AB=________.


大约在两千四五百年前，如图1墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是6cm，则蜡烛火焰的高度是________cm.


如图，扇形纸扇完全打开后，外侧两竹条AB，AC夹角为120∘，扇面BD的长为20cm，扇面（阴影部分）的面积为800π3cm2，则竹条AB的长为________cm．

三、解答题

先化简，再求值： a−22+4a+1，其中a=2 .

如图，某飞镖游戏，A区为小圆内部，B区为大圆内小圆外部，掷到A区和B区的得分不同，每次掷中的位置用一个“×”标注．已知小红、小华有效成绩均为6次，结果小红得了54分，小华得了52分．求掷中A区，B区一次各得多少分？


在全国政协2021新年茶话会上，习近平总书记强调要发扬“三牛”精神．如图，现有三张正面印有“三牛”图案的不透明卡片A，B，C，卡片除正面图案不同外，其余均相同．将三张卡片正面向下洗匀．小吉同学从中随机抽取两张卡片，请用画树状图或列表法求小吉同学抽出的两张卡片是A和B的概率．


如图，AB是⊙O的直径，PB是⊙O的切线，连接AP交⊙O于点C．点D在⊙O上，∠CDB=45∘，求证：AB=BP .


如图，4×4正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A，B都在格点上，按下列要求作图，使得所画图形的顶点均在格点上．

(1)在图①中画一个以线段AB为边的△ABC，使其面积为3；

(2)在图②中画一个以线段AB为边的轴对称四边形ABDE，使其面积为6；

(3)在图③中画一个以线段AB为边的中心对称四边形ABFG，使其面积为6.

2021年3月29日是我国第26个“全国中小学生安全教育日”．某校随机抽取了八年级学生的10%进行了一次安全知识测试，将这些学生的测试成绩（x）分为四个等级：优秀85≤x≤100；良好75≤x<85；及格60≤x<75；不及格0≤x<60. 并绘制成如图两幅统计图．
根据以上信息，解答下列问题：
(1)在抽取的学生中不及格人数所占的百分比是________；

(2)若抽取的学生中不及格人数为2人，估算该校八年级学生的人数约为________人，该校八年级学生中优秀等级的人数约为________人；

(3)估算该校八年级学生此次测试成绩的平均分．

某人乘车从A地去B地．如图所示，B 地在A地的正北方向，且距离A地9km，但A，B两地之间道路维修无法通过．按导航指示，车辆沿正西方向行驶至C地，再沿北偏东26∘方向行驶到达B地，求车辆共行驶了多少千米（结果精确到0.1km）．（参考数据：sin26∘=0.44，cs26∘=0.90，tan26∘=0.49）


“黄金1号”玉米种子的价格为5元/kg．如果一次购买2kg以上的种子，超过2kg部分的种子价格打8折．

(1)填表：

(2)直接写出付款金额关于购买量的函数解析式，并在给出的平面直角坐标系中画出函数图象．

如图，点P3,2在反比例函数y=kxx>0的图象上，过点P作PM//x轴交反比例函数y=2x 的图象于点M，作PN//y轴交反比例函数y=2x的图象于点N，连接MN．

(1)求k的值；

(2)求△PMN的面积；

(3)连接OM，ON，直接写出△MON的面积．

在四边形ABCD中， AB=AD=1，∠B=∠D=90∘，点E为BC上一点（不与点B，点C重合），连接AE，将△ABE沿AE翻折得到△AB′E，延长EB′交CD于点F．

(1)如图①，当∠C=90∘时，四边形ABCD的形状为________；

(2)在(1)的条件下，随着点E位置的变化， △CEF的周长是否发生变化？若变化，请说明理由；若不变化，请求出它的值；

(3)如图②，当∠C=60∘时，请直接写出△CEF的周长．

如图，在正方形ABCD中，AB=2，连接AC．P，Q两点分别从A，D同时出发，点P以每秒1个单位长度的速度沿线段AB向终点B运动；点Q沿折线D→A→C向终点C运动，在DA上的速度为每秒2个单位长度，在AC上的速度为每秒22个单位长度．在运动过程中，以AP，AQ为邻边作平行四边形APMQ．设运动时间为x秒，平行四边形APMQ和正方形ABCD重叠部分的图形面积为y．

(1)当点M在BC上时， x=________；

(2)求y关于x的函数解析式，并写出x的取值范围；

(3)连接MB．当0∘<∠MBP<90∘时，直接写出tan∠MBP=12时x的值．

如图，抛物线y=ax+22−9aa>0与x轴相交于A，B两点（点A在点B的左侧），顶点为C，连接BC．

(1)直接写出点C的坐标________（用含a的式子表示）；

(2)求点B的坐标：

(3)以BC为边，在BC边的右下方作正方形BCDE，设点D的坐标为m,n.
①当∠ABC=30∘时，求点D的坐标；
②当∠ABC=45∘时，直接写出点D的坐标：
③直接写出n关于m的函数解析式及自变量m的取值范围．
参考答案与试题解析
2020-2021学年吉林省四平市某校初三(下)5月月考数学试卷
一、选择题
1.
【答案】
D
【考点】
有理数的减法
【解析】
此题暂无解析
【解答】
解：由图可知，最高气温为8∘C，最低气温为−4∘C，
所以温差为：8−(−4)=8+4=12∘C.
故选D.
2.
【答案】
B
【考点】
科学记数法--表示较大的数
【解析】
此题暂无解析
【解答】
解：科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．
816000000=8.16×108.
故选B.
3.
【答案】
C
【考点】
轴对称图形
【解析】
直接判断各图形是否为对称图形，即可得出答案.
【解答】
解：如果一个平面图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形.
A，是轴对称图形，故A不符合题意；
B，是轴对称图形，故B不符合题意；
C，不是轴对称图形，故C符合题意；
D，是轴对称图形，故D不符合题意.
故选C.
4.
【答案】
C
【考点】
一元一次不等式的实际应用
【解析】
根据图形可得：2个小立方体的质量>3个砝码的质量，据此解答即可．
【解答】
解：由题意得：2m>3×5，
解得：m>152.
故选C．
5.
【答案】
A
【考点】
直线的性质：两点确定一条直线
【解析】
直接利用直线的性质分析得出答案．
【解答】
解：建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，
这种做法运用到的数学原理是：两点确定一条直线．
故选A.
6.
【答案】
D
【考点】
平行线的性质
等边三角形的性质与判定
【解析】
根据题意可得∠ACB为等腰三角形，边长为2cm,再由平行线的性质求出∠CAB的度数，可得∠ACB为等边三角形，即可解题．
【解答】
解：根据题意得，△ABC为等腰三角形，边长为2cm，
∵ a//b，∠1=60∘，
∴ ∠CAB=∠1=60∘，
∴ △ABC为等边三角形，
∴ △ABC的周长为：2+2+2=6cm.
故选D．
二、填空题
【答案】
1
【考点】
二次根式的性质与化简
【解析】
此题暂无解析
【解答】
解：9−2=3−2=1.
故答案为：1.
【答案】
4n
【考点】
列代数式
【解析】
直接根据条件，表示即可.
【解答】
解：原价n元，8折出售，则为0.8n元，
购买5本笔记本需要付费5×0.8n=4n(元).
故答案为：4n.
【答案】
23
【考点】
分式方程的解
【解析】
直接解分式方程，得出答案.
【解答】
解：由题意得，1x−1=−3，
解得，x=23，
经检验，x=23是原分式方程的根.
故答案为：23.
【答案】
1
【考点】
根的判别式
【解析】
利用方程有解，构造不等式，解出即可.
【解答】
解：若关于x的一元二次方程x2=c−1有实数根，
则c−1≥0，
解得c≥1，
所以c的值可以为1.
故答案为：1.
【答案】
120
【考点】
旋转的性质
等腰三角形的性质与判定
三角形内角和定理
【解析】
利用旋转后的相似关系求解
【解答】
解：设∠B′BC′=α，∠BB′C′=β，
∵B′C′⊥AB，
∴ 在△BCB′ 中，α+β=90∘①，
又AB=AB′，
∴ 在△ABB′中，α=∠AB′B=β+∠AB′C′，
∵ 在Rt△ABC中， ∠C=90∘ ，∠BAC=40∘，
∴ ∠ABC=50∘，
又∵ ∠AB′C′=∠ABC=50∘，
∴α=β+50∘②，
联立①②得β=20∘，α=70∘，
则∠B′BC=α+∠ABC=70∘+50∘=120∘.
故答案为：120.
【答案】
15
【考点】
平行四边形的性质
勾股定理
【解析】
根据平行四边形的性质，结合勾股定理，即可得出答案.
【解答】
解：∵ AE⊥DC，
∴ AD2=AE2+DE2，
又AD=BC=13，AE=12，
∴ 132=DE2+122，
∴ DE=5，
∴ AB=DC=DE+EC=5+10=15.
故答案为：15.
【答案】
4
【考点】
相似三角形的应用
【解析】
根据小孔成像的性质及相似三角形的性质求解即可．
【解答】
解：根据小孔成像的性质及相似三角形的性质可得：
蜡烛火焰的高度与火焰的像的高度的比值等于物距与像距的比值，
设蜡烛火焰的高度为xcm，
则x6=1015，
解得x=4，
即蜡烛火焰的高度为4cm.
故答案为：4．
【答案】
30
【考点】
弧长的计算
扇形面积的计算
【解析】
扇面部分的面积等于大扇形减去小扇形的面积，以此列式即可求解.
【解答】
解： 120360×π×AB2−AB−202=8003π（平方厘米），
解得AB=30cm．
故答案为：30.
三、解答题
【答案】
解：原式=a2−4a+4+4a+4
=a2+8 .
当a=2，原式=22+8=10 .
【考点】
整式的混合运算——化简求值
完全平方公式
【解析】
此题暂无解析
【解答】
解：原式=a2−4a+4+4a+4
=a2+8 .
当a=2，原式=22+8=10 .
【答案】
解：设掷中A区一次得x分，B区次得y分，
根据题意，得3x+3y=54,2x+4y=52,
解得x=10,y=8.
答：掷中A区一次得10分，掷中B区一次得8分．
【考点】
二元一次方程组的解
【解析】
此题暂无解析
【解答】
解：设掷中A区一次得x分，B区次得y分，
根据题意，得3x+3y=54,2x+4y=52,
解得x=10,y=8.
答：掷中A区一次得10分，掷中B区一次得8分．
【答案】
解：根据题意，画树状图如下：
由树状图可以看出，所有等可能出现的结果共有6种，
其中抽出的两张卡片是A和B的情况有2种．
所以P(抽出的两张卡片是A和B)=26=13 .
【考点】
列表法与树状图法
【解析】
此题暂无解析
【解答】
解：根据题意，画树状图如下：
由树状图可以看出，所有等可能出现的结果共有6种，
其中抽出的两张卡片是A和B的情况有2种．
所以P(抽出的两张卡片是A和B)=26=13 .
【答案】
证明：∵ PB是⊙O的切线，
∴ AB⊥BP .
∴ ∠ABP=90∘，
∴ ∠A+∠P=90∘ .
∵ ∠A=∠CDB=45∘，
∴ ∠P=45∘，
∴ ∠A=∠P .
∴ AB=BP .
【考点】
切线的性质
等腰三角形的性质与判定
圆心角、弧、弦的关系
【解析】

【解答】
证明：∵ PB是⊙O的切线，
∴ AB⊥BP .
∴ ∠ABP=90∘，
∴ ∠A+∠P=90∘ .
∵ ∠A=∠CDB=45∘，
∴ ∠P=45∘，
∴ ∠A=∠P .
∴ AB=BP .
【答案】
解：(1)△ABC如图所示.
(2)四边形ABDE如图所示.
(3)四边形ABFG如图所示.
【考点】
作图—应用与设计作图
【解析】
此题暂无解析
【解答】
解：(1)△ABC如图所示.
(2)四边形ABDE如图所示.
(3)四边形ABFG如图所示.
【答案】
5%
400,200
(3)所抽取学生测试成绩的平均分：
90×50%+78×25%+66×20%+42×5%=79.8（分）．
【考点】
扇形统计图
用样本估计总体
加权平均数
条形统计图
【解析】
(1)根据百分比的和等于1求解即可．
(2)首先确定总人数，根据优秀人数=总人数×优秀率计算即可；
(3)利用加权平均数求解即可．
【解答】
解：(1)在抽取的学生中不及格人数所占的百分比为：
1−20%−25%−50%=5%.
故答案为：5%.
(2)由题意得，总人数=2÷5%÷10%=400（人），
400×50%=200（人），
∴ 该校八年级学生的人数约为400人，该校八年级学生中优秀等级的人数约为200人．
故答案为：400；200.
(3)所抽取学生测试成绩的平均分：
90×50%+78×25%+66×20%+42×5%=79.8（分）．
【答案】
解：根据题意，得∠B=26∘，AB=9km．
在Rt△ABC中，tanB=ACAB，csB=ABBC，
∴ AC=AB⋅tanB=9×0.49=4.41，
BC=ABcsB=90.90=10，
∴ AC+BC=4.41+10=14.41≈14.4km .
答：车辆共行驶了14.4千米．
【考点】
解直角三角形的应用-方向角问题
【解析】
无
【解答】
解：根据题意，得∠B=26∘，AB=9km．
在Rt△ABC中，tanB=ACAB，csB=ABBC，
∴ AC=AB⋅tanB=9×0.49=4.41，
BC=ABcsB=90.90=10，
∴ AC+BC=4.41+10=14.41≈14.4km .
答：车辆共行驶了14.4千米．
【答案】
5,10,14
(2)由题意可得，
当0≤x≤2时，y=5x，
当x>2时，y=5×2+x−2×5×0.8=4x+2，
所以付款金额关于购买量的函数解析式为：
y=5x(0≤x≤2)，4x+2(x>2)，
相应的函数图象如图所示.
【考点】
一次函数的应用
一次函数的图象
分段函数
【解析】
(1)根据题意可以将表格中的数据补充完整；
(2)根据题意和表格中的数据可以写出相应的函数解析式和画出相应的函数图象．
【解答】
解：(1)设购买种子为xkg，付款金额为y元，
当x=1时，y=5×1=5元；
当x=2时，y=5×2=10元；
当x=3时，y=5×2+3−2×5×0.8=14元，
填表如下.
故答案为：5；10；14.
(2)由题意可得，
当0≤x≤2时，y=5x，
当x>2时，y=5×2+x−2×5×0.8=4x+2，
所以付款金额关于购买量的函数解析式为：
y=5x(0≤x≤2)，4x+2(x>2)，
相应的函数图象如图所示.
【答案】
解：(1)∵ 点P3,2在反比例函数y=kx的图象上，
∴ 2=k3，
解得k=6 .
(2)∵ 点P的坐标为3,2 ，PM//x轴， PN//y轴，
∴ 点M的纵坐标为2，点N的横坐标为3，
∵ 点M，N在反比例函数y=2x的图象上，
∴ 点M的坐标为1,2，点N的坐标为3,23 ，
∴ PM=2， PN=43，
∴ S△PMN=12PM⋅PN=12×2×43=43.
(3)延长PM交y轴于A，延长PN交x轴于B，
则S△AMO=S△BON=k2=1，
∴S△MON=S矩形AOBP−S△AMO−S△BNO−S△PMN
=6−1−1−43
=83.
【考点】
待定系数法求反比例函数解析式
反比例函数的应用
反比例函数图象上点的坐标特征
三角形的面积
反比例函数系数k的几何意义
【解析】
（1）利用待定系数法即可求解
利用坐标关系求得三角形两直角边的长，代入面积公式即可求解.
利用k的几何意义结合题意求解.
【解答】
解：(1)∵ 点P3,2在反比例函数y=kx的图象上，
∴ 2=k3，
解得k=6 .
(2)∵ 点P的坐标为3,2 ，PM//x轴， PN//y轴，
∴ 点M的纵坐标为2，点N的横坐标为3，
∵ 点M，N在反比例函数y=2x的图象上，
∴ 点M的坐标为1,2，点N的坐标为3,23 ，
∴ PM=2， PN=43，
∴ S△PMN=12PM⋅PN=12×2×43=43.
(3)延长PM交y轴于A，延长PN交x轴于B，
则S△AMO=S△BON=k2=1，
∴S△MON=S矩形AOBP−S△AMO−S△BNO−S△PMN
=6−1−1−43
=83.
【答案】
正方形
(2)△CEF的周长不发生变化．
理由：连接AF，
由折叠可知AB=AB′，∠AB′E=∠B=90∘，BE=B′E．
∴ ∠AB′F=90∘．
∵ AB=AD，
∴ AB′=AD．
在Rt△AB′F和Rt△ADF中，
AF=AF，AB′=AD，
∴ Rt△AB′F≅Rt△ADFHL，
∴ B′F=DF，
∴ △CEF的周长=EC+CF+EF
=EC+CF+B′E+B′F
=EC+CF+BE+DF
=BC+CD
=1+1=2 ．
(3)连接AF，
由(2)可得，Rt△AB′F≅Rt△ADFHL，
∴ ∠DAF=∠B′AF，
由旋转的性质可得∠BAE=∠B′AE，
在四边形ABCD中，当∠C=60∘时，∠BAD=120∘，
∴ ∠FAE=∠B′AF+∠B′AE=12∠BAD=60∘，
∴ △AEF为等边三角形，
∵ AB′⊥EF，
∴ ∠EAB′=∠FAB′=30∘，
∴ ∠BAE=∠B′AE=30∘，∠DAE=90∘，
在△ABE中，∠AEB=90∘−30∘=60∘，
∴ ∠FEC=60∘，
∴ △CEF为等边三角形，
作EG⊥FC于G，
可知四边形AEGD为矩形，
∴ AD=EG=1，
∴ CF=233，
∴ △CEF的周长为3×233=23，
∴ △CEF的周长为23.
【考点】
正方形的判定
翻折变换（折叠问题）
全等三角形的性质与判定
全等三角形的性质
矩形的判定与性质
等边三角形的性质与判定
【解析】
此题暂无解析
【解答】
解：(1)∵ ∠B=∠D=90∘，
当∠C=90∘时，∠A=90∘，
又AB=AD，
∴ 四边形ABCD为正方形.
故答案为：正方形.
(2)△CEF的周长不发生变化．
理由：连接AF，
由折叠可知AB=AB′，∠AB′E=∠B=90∘，BE=B′E．
∴ ∠AB′F=90∘．
∵ AB=AD，
∴ AB′=AD．
在Rt△AB′F和Rt△ADF中，
AF=AF，AB′=AD，
∴ Rt△AB′F≅Rt△ADFHL，
∴ B′F=DF，
∴ △CEF的周长=EC+CF+EF
=EC+CF+B′E+B′F
=EC+CF+BE+DF
=BC+CD
=1+1=2 ．
(3)连接AF，
由(2)可得，Rt△AB′F≅Rt△ADFHL，
∴ ∠DAF=∠B′AF，
由旋转的性质可得∠BAE=∠B′AE，
在四边形ABCD中，当∠C=60∘时，∠BAD=120∘，
∴ ∠FAE=∠B′AF+∠B′AE=12∠BAD=60∘，
∴ △AEF为等边三角形，
∵ AB′⊥EF，
∴ ∠EAB′=∠FAB′=30∘，
∴ ∠BAE=∠B′AE=30∘，∠DAE=90∘，
在△ABE中，∠AEB=90∘−30∘=60∘，
∴ ∠FEC=60∘，
∴ △CEF为等边三角形，
作EG⊥FC于G，
可知四边形AEGD为矩形，
∴ AD=EG=1，
∴ CF=233，
∴ △CEF的周长为3×233=23，
∴ △CEF的周长为23.
【答案】
43
(2)如图①，
当0≤x≤1时， AQ=2−2x，AP=x，
∴ y=AQ⋅AP=2−2x⋅x=−2x2+2x；
如图②，
当1∵ AQ=22x−1，∠QAE=45∘，
∴ QE=2x−1，
∵ AP=x，
∴ y=AP⋅QE=x⋅2x−1=2x2−2x；
如图③，
当43∵ AQ=22x−1，
∴ CQ=22−(22x−22)=42−22x，
∵ ∠QCG=45∘，
∴ QG=4−2x，
∴ GM=QM−QG=x−4−2x=3x−4，
∴ y=S四边形APMQ−S△MFG
=2x2−2x−123x−42
=−52x2+10x−8，
综上，y=−2x2+2x,0(3)当 0∘<∠MBP<90∘，M在正方形ABCD内部，
∴ 0①当 0AP=x，AQ=2−2x=MP，BP=2−x，
tan∠MBP=MPPB=2−2x2−x=12，
解得x=23；
②当 1作MN⊥AB于点N，
则MN=22⋅22x−1=2x−2 ，
易知∠MPN=45∘，△PMN为等腰直角三角形 ，
∴PN=MN=2x−2，
∴NB=2−AP−PN=2−x−2x−2=4−3x，
∴tan∠MBP=MNNB=2x−24−3x=12，
解得x=87，
综上， x=23或x=87．
【考点】
动点问题
勾股定理
相似三角形的性质与判定
四边形综合题
【解析】
此题暂无解析
【解答】
解：(1)当点Q在DA上运动时，∠QAP=90∘，
则平行四边形APMQ为矩形（此时MP//BC），
当M在BC上时，Q点应在AC上运动，
如图所示，
则AP=x，AQ=22x−1，AC=22+22=22 ，
∴QC=22−22(x−1)=−22x+42，
BP=2−AP=2−x，
∵ 四边形APMQ为平行四边形，
∴MP//AC，MP=AQ=22x−1，
∴△PBM∽△ABC．
∴PBAB=PMAC⇒PBPM=ABAC=22，
∴2−x22x−1=22，
∴x=43．
故答案为：43．
(2)如图①，
当0≤x≤1时， AQ=2−2x，AP=x，
∴ y=AQ⋅AP=2−2x⋅x=−2x2+2x；
如图②，
当1∵ AQ=22x−1，∠QAE=45∘，
∴ QE=2x−1，
∵ AP=x，
∴ y=AP⋅QE=x⋅2x−1=2x2−2x；
如图③，
当43∵ AQ=22x−1，
∴ CQ=22−(22x−22)=42−22x，
∵ ∠QCG=45∘，
∴ QG=4−2x，
∴ GM=QM−QG=x−4−2x=3x−4，
∴ y=S四边形APMQ−S△MFG
=2x2−2x−123x−42
=−52x2+10x−8，
综上，y=−2x2+2x,0(3)当 0∘<∠MBP<90∘，M在正方形ABCD内部，
∴ 0①当 0AP=x，AQ=2−2x=MP，BP=2−x，
tan∠MBP=MPPB=2−2x2−x=12，
解得x=23；
②当 1作MN⊥AB于点N，
则MN=22⋅22x−1=2x−2 ，
易知∠MPN=45∘，△PMN为等腰直角三角形 ，
∴PN=MN=2x−2，
∴NB=2−AP−PN=2−x−2x−2=4−3x，
∴tan∠MBP=MNNB=2x−24−3x=12，
解得x=87，
综上， x=23或x=87．
【答案】
−2,−9a
(2)当y=0时，ax+22−9a=0，
解得：x1=1, x2=−5，
∵点A在点B的左侧，
∴点B的坐标为1,0 .
解：①当∠ABC=30∘时，过点C作CM⊥AB于点M，
过点D作DN⊥MC交MC的延长线于点N．
在Rt△BMC中，∠MBC=30∘，BM=3，∴CM=3，
∵∠MBC+∠MCB=90∘, ∠NCD+∠MCB=90∘,
∴∠MBC=∠NCD,
∵∠BMC=∠CND, BC=CD,
∴△BMC≅△CND,
∴CN=BM=3，DN=CM=3,
∴MN=3+3，OM−DN=2−3，
∴点D的坐标为−2+3,−3−3 ；
②当∠ABC=45∘时，过点C作CM⊥AB于点M，
过点D作DN⊥MC交MC的延长线于点N．
在Rt△BMC中，∠MBC=45∘，BM=3，∴CM=3,
∵∠MBC+∠MCB=90∘, ∠NCD+∠MCB=90∘,
∴∠MBC=∠NCD，
∵∠BMC=∠CND, BC=CD,
∴△BMC≅△CND,
∴CN=BM=3，DN=CM=3,
∴MN=3+3=6，DN−OM=3−2=1，
∴点D的坐标为1,−6 ；
③过点C作CM⊥AB于点M，
过点D作DN⊥MC交MC的延长线于点N．
∵∠MBC+∠MCB=90∘, ∠NCD+∠MCB=90∘,
∴∠MBC=∠NCD，
∵∠BMC=∠CND, BC=CD,
∴△BMC≅△CND,
∴CN=BM=3，DN=CM,
∴MN=MC+CN=MC+3，OM−DN=2−CM，
∵点D的坐标为m,n,
∴MC+3=−n，2−CM=−m,
∴n=−m−5.
要以BC边的右下方作正方形BCDE，则点D必须在对称轴的右侧，
∵抛物线y=ax+22−9aa>0的对称轴为：x+2=0，即x=−2，
∴m>−2.
∴ n=−m−5m>−2.
【考点】
二次函数y=ax^2 、y=a（x-h）^2+k (a≠0)的图象和性质
抛物线与x轴的交点
全等三角形的性质与判定
二次函数图象上点的坐标特征
二次函数图象与几何变换
【解析】
本题可根据抛物线解析式得到对称轴，再代入求对应的纵坐标，得到顶点的坐标。
本题可根据抛物线与x轴的交点，观察图象得到点B的坐标为1,0。
本题根据直角三角形的性质，余角的性质，全等三角形的判定及其性质，及二次函数图象上的点的坐标特征，及其与几何的变换得到答案。
【解答】
解：(1)抛物线y=ax+22−9aa>0的对称轴为：x=−2,
当x=−2时，y=a−2+22−9a=−9a,
故顶点C的坐标为−2,−9a.
故答案为：−2,−9a .
(2)当y=0时，ax+22−9a=0，
解得：x1=1, x2=−5，
∵点A在点B的左侧，
∴点B的坐标为1,0 .
解：①当∠ABC=30∘时，过点C作CM⊥AB于点M，
过点D作DN⊥MC交MC的延长线于点N．
在Rt△BMC中，∠MBC=30∘，BM=3，∴CM=3，
∵∠MBC+∠MCB=90∘, ∠NCD+∠MCB=90∘,
∴∠MBC=∠NCD,
∵∠BMC=∠CND, BC=CD,
∴△BMC≅△CND,
∴CN=BM=3，DN=CM=3,
∴MN=3+3，OM−DN=2−3，
∴点D的坐标为−2+3,−3−3 ；
②当∠ABC=45∘时，过点C作CM⊥AB于点M，
过点D作DN⊥MC交MC的延长线于点N．
在Rt△BMC中，∠MBC=45∘，BM=3，∴CM=3,
∵∠MBC+∠MCB=90∘, ∠NCD+∠MCB=90∘,
∴∠MBC=∠NCD，
∵∠BMC=∠CND, BC=CD,
∴△BMC≅△CND,
∴CN=BM=3，DN=CM=3,
∴MN=3+3=6，DN−OM=3−2=1，
∴点D的坐标为1,−6 ；
③过点C作CM⊥AB于点M，
过点D作DN⊥MC交MC的延长线于点N．
∵∠MBC+∠MCB=90∘, ∠NCD+∠MCB=90∘,
∴∠MBC=∠NCD，
∵∠BMC=∠CND, BC=CD,
∴△BMC≅△CND,
∴CN=BM=3，DN=CM,
∴MN=MC+CN=MC+3，OM−DN=2−CM，
∵点D的坐标为m,n,
∴MC+3=−n，2−CM=−m,
∴n=−m−5.
要以BC边的右下方作正方形BCDE，则点D必须在对称轴的右侧，
∵抛物线y=ax+22−9aa>0的对称轴为：x+2=0，即x=−2，
∴m>−2.
∴ n=−m−5m>−2.购买量/kg
1
2
3
⋯
付款金额/元
________
________
________
⋯
购买量/kg
1
2
3
…
付款金额/元
5
10
14
…