

2022年陕西省宝鸡市渭滨区初中学业水平模拟考试数学试题(四)(word版含答案)
展开初中学业水平模拟考试数学试卷
第一部分(选择题 共24分)
一.选择题(共8小题,每小题3分,计24分)
1.计算:(−13)×3等于( )
A.4 B.﹣4 C.1 D.﹣1
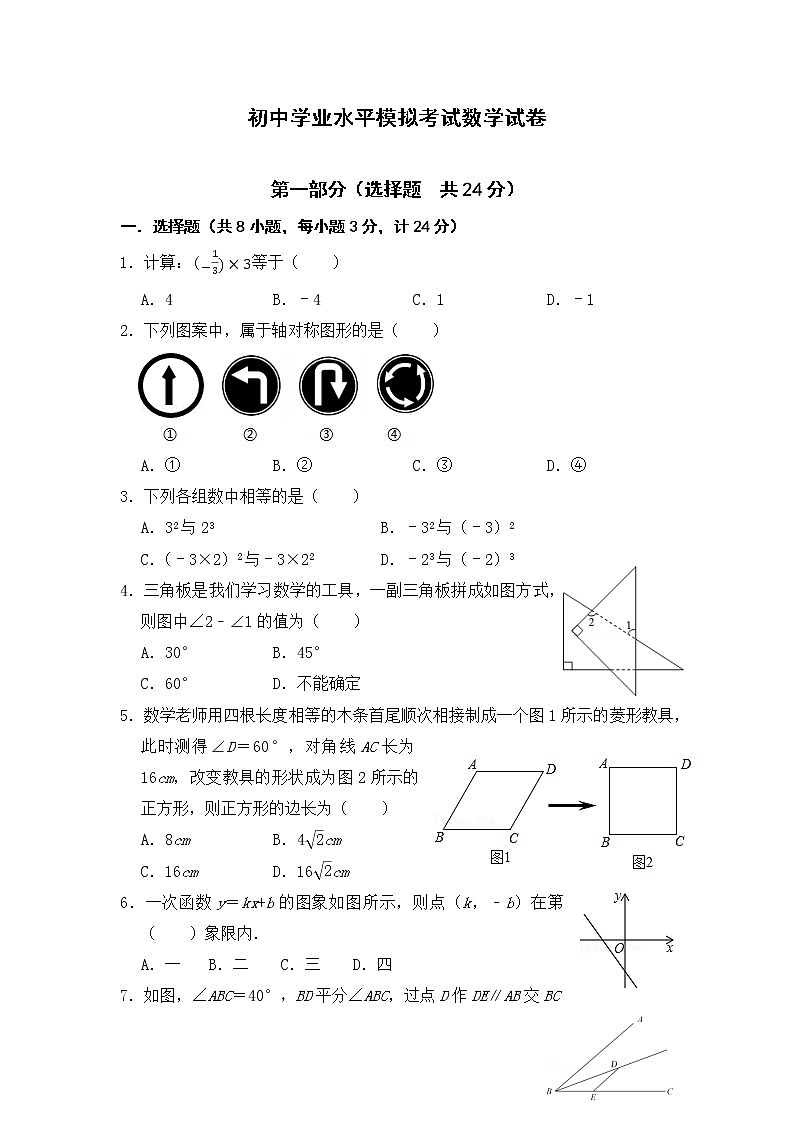
2.下列图案中,属于轴对称图形的是( )
A.① B.② C.③ D.④
3.下列各组数中相等的是( )
A.32与23 B.﹣32与(﹣3)2
C.(﹣3×2)2与﹣3×22 D.﹣23与(﹣2)3
4.三角板是我们学习数学的工具,一副三角板拼成如图方式,则图中∠2﹣∠1的值为( )
A.30° B.45°
C.60° D.不能确定
5.数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得∠D=60°,对角线AC长为16cm,改变教具的形状成为图2所示的正方形,则正方形的边长为( )
A.8cm B.42cm
C.16cm D.162cm
6.一次函数y=kx+b的图象如图所示,则点(k,﹣b)在第( )象限内.
A.一 B.二 C.三 D.四
7.如图,∠ABC=40°,BD平分∠ABC,过点D作DE∥AB交BC于点E,若点F在AB上,且满足DF=DE,则∠DFB的度数为( )
A.20° B.140°
C.40°或140° D.20°或140°
8.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:
x
…
﹣2
﹣1
0
1
2
…
y=ax2+bx+c
…
t
m
﹣2
﹣2
n
…
且当x=−12时,与其对应的函数值y>0,有下列结论:
①abc<0;②m=n;③﹣2和3是关于x的方程ax2+bx+c=t的两个根;④a<83.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
第二部分(非选择题 共96分)
二.填空题(共5小题,每小题3分,计15分)
9.分解因式:﹣9a2+b2= .
10.)若一个多边形每一个内角都是与它相邻的外角的4倍,则此多边形的边数为 .
11.古代名著《算学启蒙》中有一题:良马日行二百里.驽马日行一百二十里.驽马先行一十二日,问良马几何追及之.意思是:跑得快的马每天走200里,跑得慢的马每天走120里.慢马先走12天,快马几天可追上慢马?则快马
天可追上慢马.
12.如图,点B在反比例函数y=6x(x>0)的图象上,点C在反比例函数y=−2x(x>0)的图象上,且BC∥y轴,AC⊥BC,垂足为点C,交y轴于点A,则△ABC的面积为 .
13.(3分)如图.A(3,0).动点B到点M(3,4)的距离为1,连接BO,BO的中点为C,则线段AC的最小值为 .
三.解答题(共13小题,满分81分)
14.(本题满分5分)
计算:(12)0+|−8|×tan60°﹣616.
15.(本题满分5分)
解不等式组:4(x−1)>3x−21+x2+1−x3≥1.
16.(本题满分5分)
解方程:3x−2−x2−x=−2.
17.(本题满分5分)
已知:如图,∠MON及边ON上一点A.
求作:在∠MON内部的点P,使得PA⊥ON,且点P到∠MON两边的距离相等.
18.(本题满分5分)
如图,在△ABC中,AB=AC,BD=CF,BE=CD,∠FDE=58°,求∠A的度数.
19.(本题满分5分)
为积极响应“文明城区”创建工作,某校六年级学生组建了一支“垃圾分类”志愿者服务队.报名时男生人数是女生人数的23,活动时又有3名男生加入,同时有3名女生有事离开,此时男生人数是女生人数的34,那么原来报名时志愿者服务队中男生、女生各有多少人?
20.(本题满分5分)
国庆期间,甲、乙两人分别从《长津湖》、《我和我的父辈》、《皮皮鲁与鲁西西》三部电影中随机选择两部观看.
(1)甲选择《长津湖》、《我和我的父辈》观看的概率为 ;
(2)求甲、乙两人选择观看的两部电影恰好相同的概率.
21.(本题满分6分)港珠澳大桥,从2009年开工建造,于2018年10月24日正式通车.其全长55公里,连接港珠澳三地,集桥、岛、隧于一体,是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知3≈1.73,tan20°≈0.36,结果精确到0.1)
22.(本题满分7分)开展党史学习教育,是党中央因时因势作出的重大决策,是大力推进红色基因传承的重要举措,是凝聚智慧力量奋进新征程的现实需要.某学校在党员教师中开展了学习党史知识竞赛,将参赛的甲,乙两组党员教师成绩整理如下:
整理数据:
甲组:6,7,7,8,9,10,10,10,9,8
乙组:7,5,6,6,10,10,10,9,10,9
分析数据:
组别
平均数(分)
中位数(分)
众数(分)
甲组
8.4
b
d
乙组
a
c
e
根据以上信息解答下列问题:
(1)a= ,b= ,c= ,d= ,e= ;
(2)学校计划从每个组选5人代表学校参加区党委组织的党史知识竞赛,甲组张老师的成绩为8分,请从表格中选择合适的统计量判断张老师能否代表学校参加;
(3)请你从“平均数”,“中位数”,“众数”中任选一个角度对甲、乙两组党员的成绩进行评价.
23.(本题满分7分)研学旅行继承和发展了我国传统游学,“读万卷书,行万里路”的教育理念和人文精神,成为素质教育的新内容和新方式,提升了中小学生的自理能力,创新精神和实践能力.某校组织甲、乙两班学生分别乘坐两辆校车从学校出发,前往300km外的红色革命圣地﹣﹣延安,开展“传承红色基因 争做时代新人”研学旅行,已知乙班比甲班晚出发1.5h,且乙班以80km/h的速度行驶了1h后,提高了速度,并以提高后的速度匀速行驶至终点.如图,线段OA表示甲班离学校的距离y甲(km)与行驶时间x(h)之间的函数关系;折线BCD表示乙班离学校的距离y乙(km)与甲班行驶时间x(h)之间的函数关系,请根据图象解答下列问题:
(1)图中m= ,n= ;
(2)求线段CD所在直线的函数表达式;
(3)乙班出发多久后追上甲班?此时两班距离延安有多远?
24.(本题满分8分)如图,在⨀O中,AB为直径,BC为弦.过AC延长线上一点D,作DF⊥BO于点F,交BC于点G,交⨀O于点H,点I是DG的中点,连接CI.
(1)判断CI与⨀O的位置关系,并说明理由;
(2)连接CH,若∠GCH=2∠B,CI=6,CH=4,求HI的长.
25.(本题满分8分)如图,已知一次函数y=kx﹣2的图象与x轴交于点A,与y轴交于点B,二次函数y=x2+bx+c经过点B,且与一次函数y=kx﹣2的图象交于点C(6,4).
(1)求一次函数与二次函数的解析式.
(2)在y轴上是否存在点M,使得以点B,M,C为顶点的三角形与△BAO相似?若存在,请求出点M的坐标;若不存在,请说明理由.
26.(本题满分10分)如图,在矩形ABCD中,CD=3cm,BC=4cm,连接BD,并过点C作CN⊥BD,垂足为N,直线l垂直BC,分别交BD、BC于点P、Q.直线l从AB出发,以每秒1cm的速度沿BC方向匀速运动到CD为止;点M沿线段DA以每秒1cm的速度由点D向点A匀速运动,到点A为止,直线l与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN= ;(直接写答案,不需要说明理由)
(2)如图1,连接PM和QN,当四边形MPQN为平行四边形时,求t的值;
(3)在整个运动过程中,当t为何值时,△PMN的面积取得最大值,最大值是多少?
初中学业水平模拟考试数学试卷参考答案
一.选择题(共8小题,满分24分,每小题3分)
1—4.DADB; 2—4.CBCB
二.填空题(共5小题,满分15分,每小题3分)
9.(b+3a)(b﹣3a); 10. 十; 11. 18; 12. 4; 13. 2
三.解答题(共13小题,满分81分)
14.(5分)
解:原式=1+22×3−6×66
=1+26−6
=1+6.………………5分
15.(5分)
解:解不等式4(x﹣1)>3x﹣2,得:x>2,………………2分
解不等式1+x2+1−x3≥1,得:x≥1, ………………4分
则不等式组的解集为x>2. ………………5分
16.
解:原方程化为:
3x−2+xx−2=−2,
两边同乘(x﹣2),得:
3+x=﹣2(x﹣2),
去括号得:3+x=﹣2x+4,
移项合并得:3x=1,
解得:x=13, ………………4分
经检验,x=13是原方程的解.………………5分
17.(5分)
解:如图所示,点P即为所求.………………5分
18.(5分)
解:∵AB=AC,
∴∠B=∠C, ………………1分
在△BED与△CDF中,
BD=CF∠B=∠CBE=CD,
∴△BED≌△CDF(SAS), ………………3分
∴∠BED=∠CDF,
∵∠EDF=58°,
∴∠BDE+∠CDF=122°,
∴∠BDE+∠BED=122°,
∴∠B=58°,
∴∠C=58°, ………………4分
∴∠A=180°﹣∠B﹣∠C=64°. ………………5分
19.(5分)
解:设原来报名时志愿者服务队中有女生x人,则有男生23x人,………………1分
根据题意得23x+3=34(x﹣3), ………………3分
解得x=63, ………………4分
所以23×63=42(人),
答:原来报名时志愿者服务队中有男生42人、女生63人.………………5分
20.(5分)
解:(1)将《长津湖》、《我和我的父辈》、皮皮鲁与鲁西西》三部电影分别用字母A、B、C表示,
画树状图为:
………………1分
共有6种等可能的结果,其中AB、BA占2种,
所以甲选择《长津湖》、《我和我的父辈》观看的概率=26=13;
故答案为13; ………………2分
(2)将《长津湖》、《我和我的父辈》、皮皮鲁与鲁西西》三部电影分别用字母A、B、C表示.
画树状图为:
………………4分
共有9种等可能的结果,其中AB、BA占2种,其中甲、乙两人选择观看的两部电影相同的结果有3种,
所以甲、乙两人选择观看的两部电影恰好相同的概率=39=13. ………………5分
21.(6分)
解:在Rt△ADC中,
∵tan30°=ADCD,CD=100米,
∴AD=tan30°•CD=33×100≈57.7(米), ………………2分
在Rt△BDC中,
∵tan20°=BDCD,CD=100米,
∴BD=tan20°•CD≈0.36×100=36(米), ………………5分
∴AB=57.7+36=93.7(米). ………………6分
22.(7分)
解:(1)由题可得:b=8.5,c=9,d=10,e=10,
而a=(7+5+6+6+10+10+10+9+10+9)÷10=8.2,
故答案为:8.2,8.5,9,10,10; ………………4分
(2)甲组的中位数为8.5分,而张老师的成绩为8分,低于中间水平.因为每组抽取半数教师,所以张老师不能代表学校参加; ………………5分
(3)平均数:甲组党员的平均成绩为8.4分,乙组党员的平均成绩为8.2分,说明甲组党员平均水平略高于乙组党员;
中位数:甲组党员成绩的中位数为8.5分,乙组党员成绩的中位数为9分,说明甲组党员的中间水平略低于乙组党员的中间水平;
众数:甲乙两组党员成绩的众数都是10分,但甲组党员满分的人数略低于乙组党员满分的人数. ………………7分
23.(7分)
解:(1)∵乙班比甲班晚出发1.5h,且乙班以80km/h的速度行驶了1h后,提高了速度,
∴m=1.5+1=2.5,n=80,
故答案为:2.5,80; ………………2分
(2)设线段CD所在直线的函数表达式是y=kx+b,
根据题意得:2.5k+b=804.5k+b=300,
解得:k=110b=−195,
则线段CD所在直线的函数表达式为:y=110x﹣195(2.5≤x≤4.5);………………4分
(3)设OA的解析式是:y=mx,
根据题意得:5m=300,
解得:m=60,
则函数解析式是:y=60x,
根据题意得:y=110x−195y=60x,
解得:x=3.9y=234.
则乙班出发后经过3.9﹣1.5=2.4(h)追上甲班,
此时两班距离延安有300﹣234=66(km).
答:乙班出发后经过2.4h追上甲班,此时两班距离延安有66km.………………7分
24.(8分)
解:(1)连接OC,如下图所示,
∵DF⊥BO于点F,
∴∠B+∠BGF=90°,
∵AB为直径,
∴∠ACB=90°, ………………1分
∵I为DG的中点,
∴CI=DI=GI,
∴∠IGC=∠ICG, ………………2分
∵OB=OC,
∴∠B=∠BCO,
∵∠BGF=∠IGC,
∴∠BCO+∠ICG=90°,
∴CI⊥CO, ………………3分
∴CI为⨀O的切线; ………………4分
(2)连接CH和CO,如下图所示,
∵∠DCI+∠ICG=90°,∠ICG+∠BCO=90°,
∴∠DCI=∠BCO, ………………5分
∵∠B=∠BCO,
∵CI=DI,
∴∠D=∠DCI,
∴∠D=∠B,
∴∠A=∠DGC, ………………6分
∵∠IGC=∠ICG,∠A=∠OCA,
∴∠ICG=∠OCA,
∴△ICG∽△OCA,
∵∠GCH=2∠B,∠AOC=2∠B,
∴∠GCH=∠AOC,
∴△GCH∽△AOC,
∴△ICG∽△CHG,CG=CH=4,
∴64=IGCG=CGHG,
∴IG=6,HG=83, ………………7分
∴HI=IG﹣HG=6−83=103. ………………8分
25.(8分)
解:(1)∵一次函数y=kx﹣2的图象与y轴交于点B,
∴当x=0时,y=﹣2,
∴B(0,﹣2),
又∵一次函数y=kx﹣2的图象过点C(6,4),
∴4=6k﹣2,
∴k=1,
∴一次函数解析式为:y=x﹣2, ………………2分
又∵二次函数y=x2+bx+c过点B、C,将其坐标代入得:
36+6b+c=4c=−2,
解得:b=−5c=−2,
∴二次函数的解析式为:y=x2﹣5x﹣2; ………………4分
(2)存在,理由如下:
∵一次函数y=x﹣2的图象与x轴交于点A,
∴当y=0时,x=2,
∴A(0,2),
由(1)知,B(0,﹣2),
∴OA=2,OB=2,∠AOB=90°,
在Rt△BAO中,AB=22+22=22,
同理,由勾股定理可求:BC=(6−0)2+(4+2)2=62, ………………5分
①当点M为直角顶点时,CM⊥y轴,CM∥OA,如图所示:
∴∠MCB=∠OAB,∠MBC=∠OBA,
∴△CMB∽△AOB,
∴BMBO=BCBA,即BM2=6222,
∴BM=6,
∴MO=BM﹣BO=6﹣2=4,
∴M(0,4), ………………6分
②当点C为直角顶点时,如图所示:
∵CM⊥BC,
∴∠MCB=∠AOB=90°,∠MBC=∠ABO,
∴△MCB∽△AOB,
∴BCBO=BMAB,即622=BM22,
∴BM=12,
∴MO=BM﹣BO=12﹣2=10,
∴M(0,10),
综上,以点B,M,C为顶点的三角形与△BAO相似时,点M的坐标为(0,4)或(0,10). ………………8分
26.(10分)
解:(1)∵四边形ABCD是矩形
∴BC=AD=4cm,∠BCD=90°=∠A,
∴BD=BC2+CD2=42+32=5(cm),
∵S△BCD=12BC×CD=12×BD×CN
∴CN=BC×CDBD=4×35=125(cm),
故答案为:125cm; ………………3分
(2)在Rt△CDN中,DN=CD2−CN2=32−(125)2=95(cm),
∵四边形MPQN为平行四边形,
∴PQ∥MN,且PQ⊥BC,AD∥BC,
∴MN⊥AD,
∴MN∥AB,
∴△DMN∽△DAB,
∴DMAD=DNBD,即DM4=955,
解得:DM=3625(cm),
∴t=3625s; ………………6分
(3)∵BD=5,DN=95,
∴BN=BD﹣DN=165,
如图1,过点M作MH⊥BD于点H,
∵sin∠MDH=sin∠BDA,
∴MHMD=ABBD,
即MHt=35,
∴MH=35t,
当0<t<6425,
∵BQ=t,
∴BP=54t,
∴PN=BD﹣BP﹣DN=5−95−54t=165−54t,
∴S△PMN=12×PN×MH=12×35t×(165−54t)=−38t2+2425t,
∴当t=3225s时,S△PMN有最大值,且最大值为384625,
当t=6425s时,点P与点N重合,点P,点N,点M不构成三角形;
当6425<t≤4时,如图2,
∴PN=BP﹣BN=54t−165,
∴S△PMN=12×PN×MH=12×35t×(54t−165)=38t2−2425t,
当6425<t≤4时,S△PMN随t的增大而增大,
∴当t=4时,S△PMN最大值为5425,
∵5425>384625,
∴t=4s时,△PMN的面积取得最大值,最大值为5425. ………………10分
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/12/1 16:40:41;用户:宝鸡文理学院附中;邮箱:wenlifz@xyh.号:41820414
2022年陕西省宝鸡市渭滨区初中学业水平模拟考试数学试题(二)(word版含答案): 这是一份2022年陕西省宝鸡市渭滨区初中学业水平模拟考试数学试题(二)(word版含答案),共31页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年陕西省宝鸡市渭滨区初中学业水平模拟考试数学试题(三)(word版含答案): 这是一份2022年陕西省宝鸡市渭滨区初中学业水平模拟考试数学试题(三)(word版含答案),共13页。试卷主要包含了计算−3×5=,下列运算正确的是,如图所示,在边长为1的小正方形,分解因式等内容,欢迎下载使用。
2022年陕西省宝鸡市渭滨区初中学业水平模拟考试数学试题(五)(word版含答案): 这是一份2022年陕西省宝鸡市渭滨区初中学业水平模拟考试数学试题(五)(word版含答案),共21页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。












