2022年中考数学三轮冲刺《函数实际问题》冲刺练习五（含答案）

这是一份2022年中考数学三轮冲刺《函数实际问题》冲刺练习五（含答案），共7页。试卷主要包含了5，2，5元．，6万元等内容，欢迎下载使用。
某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种，如图是某天恒温系统从开启到关闭及关闭后，大棚里温度y（℃）随时间x（h）变化的函数图象，其中AB段是恒温阶段，BC段是双曲线y=的一部分.
请根据图中信息解答下列问题：
（1）求0到2小时期间y随x的函数解析式；
（2）恒温系统在一天内保持大棚内温度不低于15℃的时间有多少小时？
甲、乙两人分别站在相距6m的A，B两点练习打羽毛球，已知羽毛球飞行的路线为抛物线的一部分，甲在离地面1m的C处发出一球，乙在离地面1.5m的D处成功击球，球飞行过程中的最高点H与甲的水平距离AE为4m.现以点A为原点，直线AB为x轴，建立平面直角坐标系(如图所示).求羽毛球飞行的路线所在的抛物线的函数表达式及飞行的最大高度.
某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销.据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式；
(2)求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
(3)如果该企业要使每天的销售利润不低于4000元，那么销售单价应控制在什么范围内？
某玩具厂在圣诞节期间准备生产A、B两种玩具共80万套，两种玩具的成本和售价如下表：
(1)若该厂所筹集资金为2180万元，且所筹资金全部用于生产，则这两种玩具各生产多少万套？
(2)设该厂生产A种玩具x万套，两种玩具所获得的总利润为w万元，请写出w与x的关系式。
(3)由于资金短缺，该厂所筹集的资金有限，只够生产A种49万套、B种31万套或者A种50万套、B种30万套.但根据市场调查，每套A种玩具的售价将提高a元(a＞0)，B种玩具售价不变，且所生产的玩具可全部售出，该玩具厂将如何安排生产才能获得最大利润？
某网店尝试用单价随天数而变化的销售模式销售一种商品，利用30天的时间销售一种成本为10元/件的商品售后，经过统计得到此商品单价在第x天（x为正整数）销售的相关信息，如表所示：
（1）请计算第几天该商品单价为25元/件？
（2）求网店销售该商品30天里所获利润y（元）关于x（天）的函数关系式；
（3）这30天中第几天获得的利润最大？最大利润是多少？
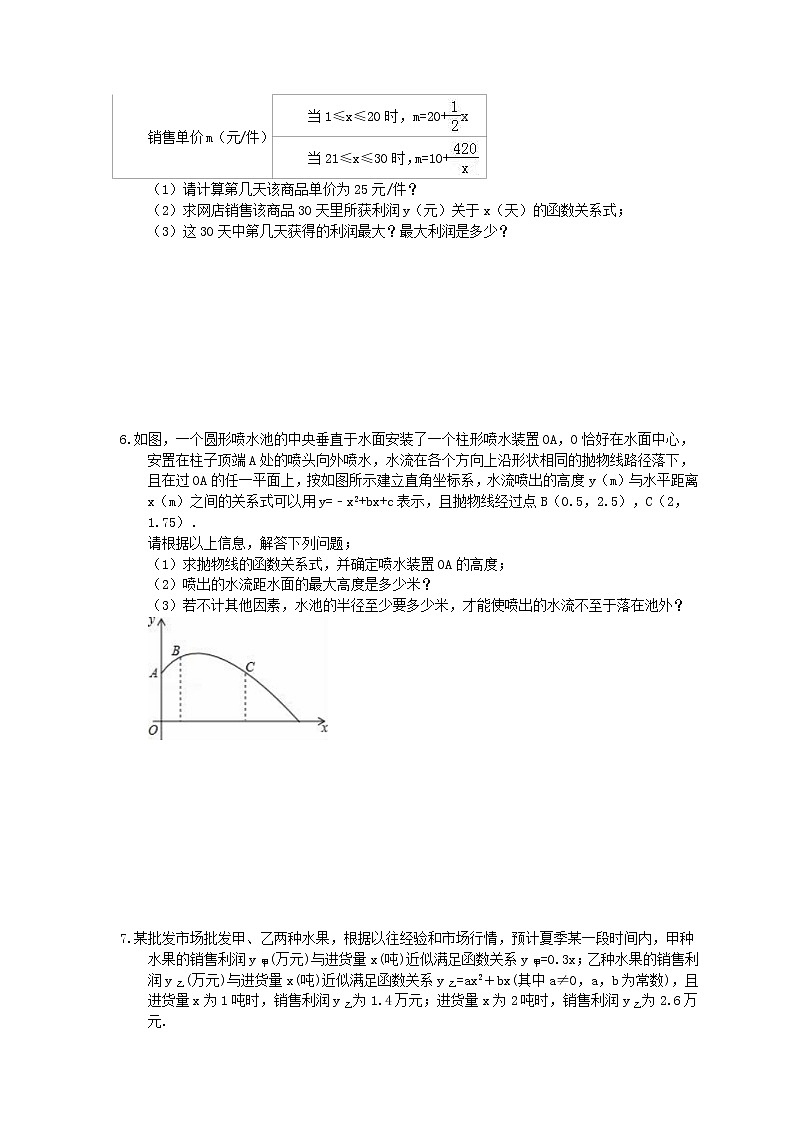
如图，一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA，O恰好在水面中心，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA的任一平面上，按如图所示建立直角坐标系，水流喷出的高度y（m）与水平距离x（m）之间的关系式可以用y=﹣x2+bx+c表示，且抛物线经过点B（0.5，2.5），C（2，1.75）．
请根据以上信息，解答下列问题；
（1）求抛物线的函数关系式，并确定喷水装置OA的高度；
（2）喷出的水流距水面的最大高度是多少米？
（3）若不计其他因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外？
某批发市场批发甲、乙两种水果，根据以往经验和市场行情，预计夏季某一段时间内，甲种水果的销售利润y甲(万元)与进货量x(吨)近似满足函数关系y甲=0.3x；乙种水果的销售利润y乙(万元)与进货量x(吨)近似满足函数关系y乙=ax2＋bx(其中a≠0，a，b为常数)，且进货量x为1吨时，销售利润y乙为1.4万元；进货量x为2吨时，销售利润y乙为2.6万元.
(1)求y乙(万元)与x(吨)之间的函数关系式；
(2)如果市场准备进甲、乙两种水果共10吨，设乙种水果的进货量为t吨，请你写出这两种水果所获得的销售利润之和W(万元)与t(吨)之间的函数关系式，并求出这两种水果各进多少吨时获得的销售利润之和最大，最大利润是多少？
某花店专卖某种进口品种的月季花苗，购进时每盆花苗的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600盆，而销售单价每上涨1元，就会少售出10盆．
（1）设该种月季花苗的销售单价在40元的基础上涨了x元（x＞0），若要使得花店每盆的利润不得低于14元，且花店要完成不少于540盆的销售任务，求x的取值范围；
（2）在（1）问前提下，若设花店所获利润为W元，试用x表示W，并求出当销售单价为多少时W最大，最大利润是什么？
\s 0 答案解析
解：（1）当x=12时，y==20，B（12，20），
∵AB段是恒温阶段，
∴A（2，12），
设函数解析式为y=kx+b，代入（0，10），和（2，20），得
，解得，
0到2小时期间y随x的函数解析式y=5x+10；
（2）把y=15代入y=5x+10，即5x+10=15，解得x1=1，
把y=15代入y=，即15=，解得x2=16，
∴16﹣1=15，
答：恒温系统在一天内保持大棚内温度不低于15℃的时间有15小时.
解：由题意得C(0，1)，D(6，1.5)，抛物线的对称轴为直线x=4.
设抛物线的函数表达式为y=ax2+bx+1(a≠0)，
根据题意得 SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 .
∴羽毛球飞行的路线所在的抛物线的函数表达式为y=- SKIPIF 1 < 0 x2+ SKIPIF 1 < 0 x+1.
∵y=- SKIPIF 1 < 0 x2+ SKIPIF 1 < 0 x+1=- SKIPIF 1 < 0 (x-4)2+ SKIPIF 1 < 0 ，
∴飞行的最大高度为 SKIPIF 1 < 0 m.
解：(1)y=(x﹣50)[50+5(100﹣x)]
=(x﹣50)(﹣5x+550)
=﹣5x2+800x﹣27500，
∴y=﹣5x2+800x﹣27500(50≤x≤100)；
(2)y=﹣5x2+800x﹣27500=﹣5(x﹣80)2+4500，
∵a=﹣5＜0，
∴抛物线开口向下.
∵50≤x≤100，对称轴是直线x=80，
∴当x=80时，y最大值=4500；
(3)当y=4000时，﹣5(x﹣80)2+4500=4000，
解得x1=70，x2=90.
∴当70≤x≤90时，每天的销售利润不低于4000元.
解：(1)设生产A种玩具x万套，B种玩具(80-x)万套，
根据题意得，25x×10000+28(80-x)×10000=2180×10000，
解得x=20，
80-20=60，
答：生产A种玩具20万套，B种玩具60万套。
(2)w×10000=(30-25)x×10000+(34-28)(80-x)×10000。
化简，得
w=-x+480。
即w与x的关系式是；w=-x+480。
(3)根据题意可得，获得的利润为：w=-x+480+ax。
当x=49时，w1=-49+480+49a=431+49a①；
当x=50时，w2=-50+480+50a=430+50a②。
①-②，得w1-w2=1-a。
∴当a＜1时，选择生产A种49万套、B种31万套；
当a＞1时，选择生产A种50万套、B种30万套。
即当a＜1时，玩具厂将选择生产A种49万套、B种31万套能获得最大利润；当a＞1时，玩具厂将选择生产A种50万套、B种30万套能获得最大利润。
【解答】解：（1）分两种情况
①当1≤x≤20时，将m=25代入m=20+x，解得x=10
②当21≤x≤30时，25=10+，解得x=28
经检验x=28是方程的解∴x=28答：第10天或第28天时该商品为25元/件．
（2）分两种情况
①当1≤x≤20时，y=（m﹣10）n=（20+x﹣10）（50﹣x）=﹣x2+15x+500，
②当21≤x≤30时，y=（10+﹣10）（50﹣x）=
综上所述：
（3）①当1≤x≤20时 由y=﹣x2+15x+500=﹣（x﹣15）2+，
∵a=﹣＜0，∴当x=15时，y最大值=，
②当21≤x≤30时 由y=﹣420，可知y随x的增大而减小
∴当x=21时，y最大值=﹣420=580元
∵∴第15天时获得利润最大，最大利润为612.5元．

解：(1)由题意，得eq \b\lc\{(\a\vs4\al\c1(a＋b＝1.4，,4a＋2b＝2.6.))解得eq \b\lc\{(\a\vs4\al\c1(a＝－0.1，,b＝1.5.))
∴y乙=－0.1x2＋1.5x.
(2)W=y甲＋y乙=0.3(10－t)＋(－0.1t2＋1.5t)
=－0.1t2＋1.2t＋3=－0.1(t－6)2＋6.6.
∵－0.1