2022河南省八所名校高二下学期第三次联考数学（理）试题含答案

河南省八所名校2021-2022学年高二下学期联考三

理科数学试卷

注意事项：

1、本试卷分为第1卷（选择题）和第2卷（非选择题）两部分。

2、本场考试150分钟，满分150分。

    3、答卷前考生务必将自己的姓名和考号填写在答题卡上，并使用2B铅笔填涂。

    4、考试结束后，将答题卡交回。

一、选择题(每小题5分,共60分)

1.已知复数，则复数z在复平面内对应的点位于

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

2.有一机器人的运动方程为是时间，s是位移，则该机器人在时刻时的瞬时速度为     

A.  B.  C.  D.

3.已知复数，i为虚数单位，则等于   

A.  B.  C.  D.

4.下列运算正确的个数为

，，，．

A. 0 B. 1 C. 2 D. 3

5.指数函数是R上的增函数，是指数函数，所以是R上的增函数．以上推理

A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 正确

6.已知曲线上一点，则过点P的切线的倾斜角为     

A.  B.  C.         D.

7.设函数在定义域内可导，的图象如图所示，则导函数的图象可能是

A.           B.

C.            D.

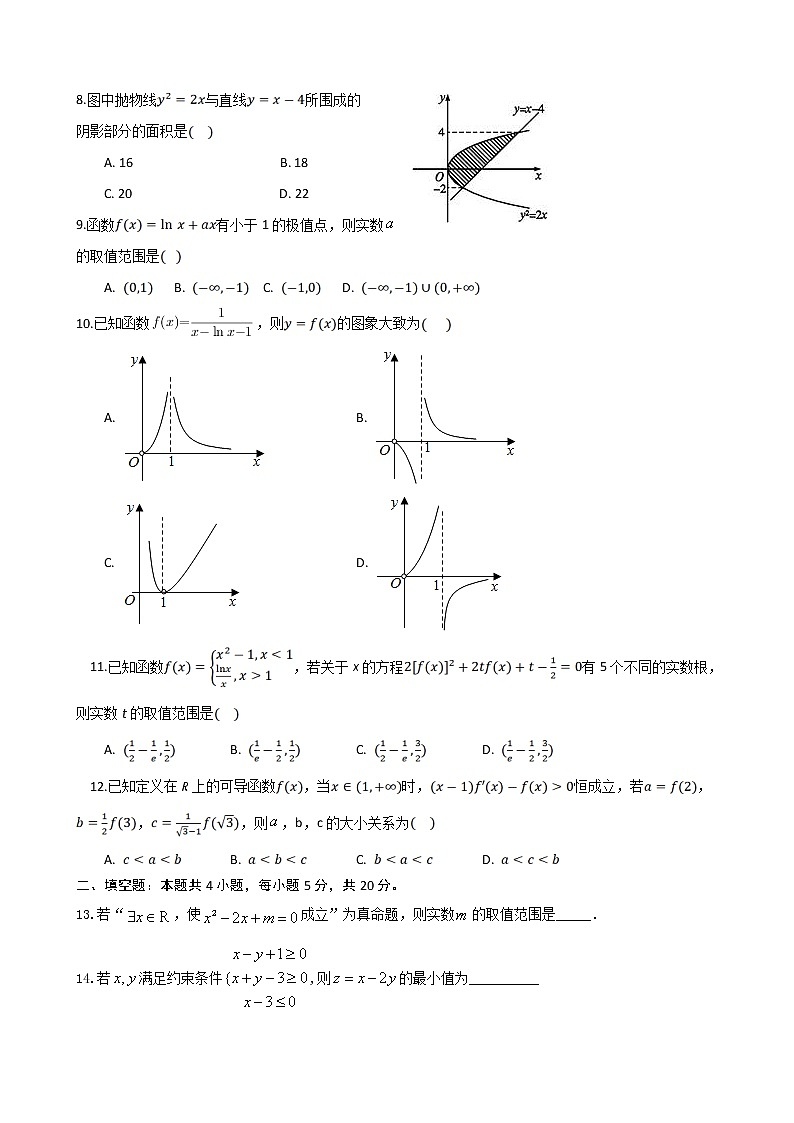
8.图中抛物线与直线所围成的

阴影部分的面积是

A. 16                     B. 18

C. 20                     D. 22

9.函数有小于1的极值点，则实数的取值范围是 

A.  B.   C.  D.

10.已知函数，则的图象大致为      

A.  B.

C.  D.

11.已知函数，若关于x的方程有5个不同的实数根，则实数t的取值范围是

A.  B.  C.  D.

12.已知定义在R上的可导函数，当时，恒成立，若，，，则，b，c的大小关系为

A.  B.  C.  D.

二、填空题：本题共4小题，每小题5分，共20分。

13.若“，使成立”为真命题，则实数的取值范围是_____．

14.若满足约束条件,则的最小值为__________

15.在平面直角坐标系中，点，若在曲线上存在点使得，则实数的取值范围为_______.

16.平面直角坐标系中,双曲线的渐近线与抛物线交于点.若的垂心为的焦点,则的离心率为__________.

三、解答题（本大题共6小题，共70分）

17．(10分)

已知函数f(x)＝x﹣lnx

（1）求曲线y＝f(x)在点（1，f(1)）处的切线方程；

（2）求函数f(x)的极值．

18．(12分)

已知抛物线：的焦点为，上的一点到焦点的距离是，

求抛物线的方程；

过作直线，交于，两点，若线段中点的纵坐标为，求直线的方程.

19．(12分)

在直三棱柱ABC﹣A1B1C1中，AB⊥AC，AB=AC=2，

A1A=4，点D是BC的中点；

（1）求异面直线A1B，AC1所成角的余弦值；

（2）求直线AB1与平面C1AD所成角的正弦值．

20．(12分)

已知，是函数的两个极值点.

（1）求的解析式；

（2）记，，若函数有三个零点，求的取值范围.

21．(12分)

如图，直角梯形与等腰直角三角形所在的平面互相

垂直，，=2，.

（1）求点C到平面的距离；

（2）线段上是否存在点F，使与平面所成角正弦值为，若存在，求出，若不存在，说明理由.

22．(12分)

设函数．

（1）求的单调区间；

（2）若a=1，k为整数，且当x>0时，恒成立，求k的最大值．（其中为的导函数．）

理科答案

13.14.1516.

17.解：（1） ，       ………………………………2分

则，，

即切线的斜率为0，              ……………………………………4分

所以曲线y＝f(x)在点（1，f(1)）处曲线的切线方程为；…………5分

（2）当时，，当时，，

所以函数在上递减，在上递增，    ………………………9分

函数的极小值为，无极大值.      ………………………10分

18.解：抛物线：的准线方程为，

由抛物线的定义可知，       ………………………………2分

解得，

的方程为．       ………………………………………………4分

由得抛物线的方程为，焦点，

设，两点的坐标分别为，，

则，     ………………………………………………………6分

两式相减，，

整理得，     ………………………………………………8分

线段中点的纵坐标为，

直线的斜率，   …………………………10分

直线的方程为，即．  ……………12分

19.解：（I）以，，为x，y，z轴建立空间直角坐标系A﹣xyz，

则可得B（2，0，0），A1（0，0，4），C1（0，2，4），D（1，1，0），

∴=（2，0，﹣4），=（0，2，4）， ………………………3分

∴cos＜，＞==

∴异面直线A1B，AC1所成角的余弦值为； …………………………6分

（II）由（I）知，=（2，0，﹣4），=（1，1，0），

设平面C1AD的法向量为=（x，y，z），

则可得，即，取x=1可得=（1，﹣1，），……9分

设直线AB1与平面C1AD所成的角为θ，则sinθ=|cos＜，＞|=

∴直线AB1与平面C1AD所成角的正弦值为 ………………………12分

20.解：（1）因为，所以………1分

根据极值点定义，方程的两个根即为，，

，代入，，可得

，解之可得，，        …………………………3分

故有；      ………………………………………4分

（2）根据题意，，，，

根据题意，可得方程在区间，内有三个实数根，

即函数与直线在区间，内有三个交点，

又因为，

则令，解得；令，解得或，

所以函数在，上单调递减，在上单调递增；…6分

又因为， ，， ，……10分

函数图象如右所示：

若使函数与直线有三个交点，

则需使，即．    …………………12分

21.解：解：如图所示，取中点，连结，，

因为三角形是等腰直角三角形，所以，

因为面面，面面面，

所以平面，又因为，

所以四边形是矩形，可得，

则，

建立如图所示的空间直角坐标系，则：

   ………………………………1分

据此可得，

设平面的一个法向量为，

则，令可得，……………………………3分

从而，又，

故求点到平面的距离．……………………5分

（2）假设存在点，，满足题意，

点在线段上，则，    ……………………………6分

即：，，，，，

据此可得：，，从而，，，，…8分

设与平面所成角所成的角为，

则，  ………………………………10分

整理可得：，

解得：或（舍去）．              ……………………………11分

据此可知，存在满足题意的点，点为的中点，即．………12分

22.解：（Ⅰ）函数的定义域为，………………1分

当时，对于恒成立，此时函数在上单调递增；

当时，由可得；由可得；

此时在上单调递减，在上单调递增；…………3分

综上所述：当时，函数的单调递增区间为，

当时，单调递减区间为，单调递增区间为，…4分

（Ⅱ）若，由可得，

因为，所以，

所以

所以对于恒成立，         ……………………………5分

令，则，

，

令，则对于恒成立，

所以在单调递增，          ……………………7分

因为，，

所以在上存在唯一的零点，

即，可得：，       ……………………9分

当时，，则，

当时，，则，

所以在上单调递减，在上单调递增，

所以，……………11分

因为，所以的最大值为.        …………………………12分