2022年重庆市中考数学第二轮复习：一次函数和反比例函数综合训练1

这是一份2022年重庆市中考数学第二轮复习：一次函数和反比例函数综合训练1，共9页。
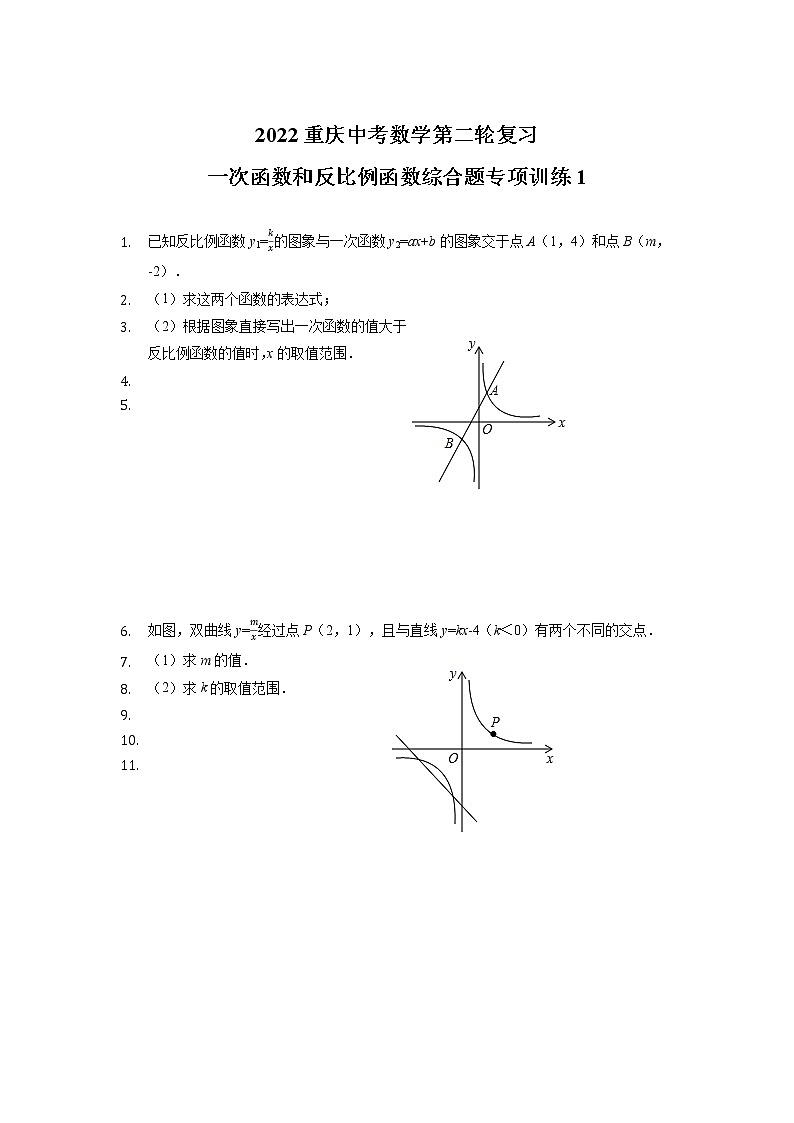
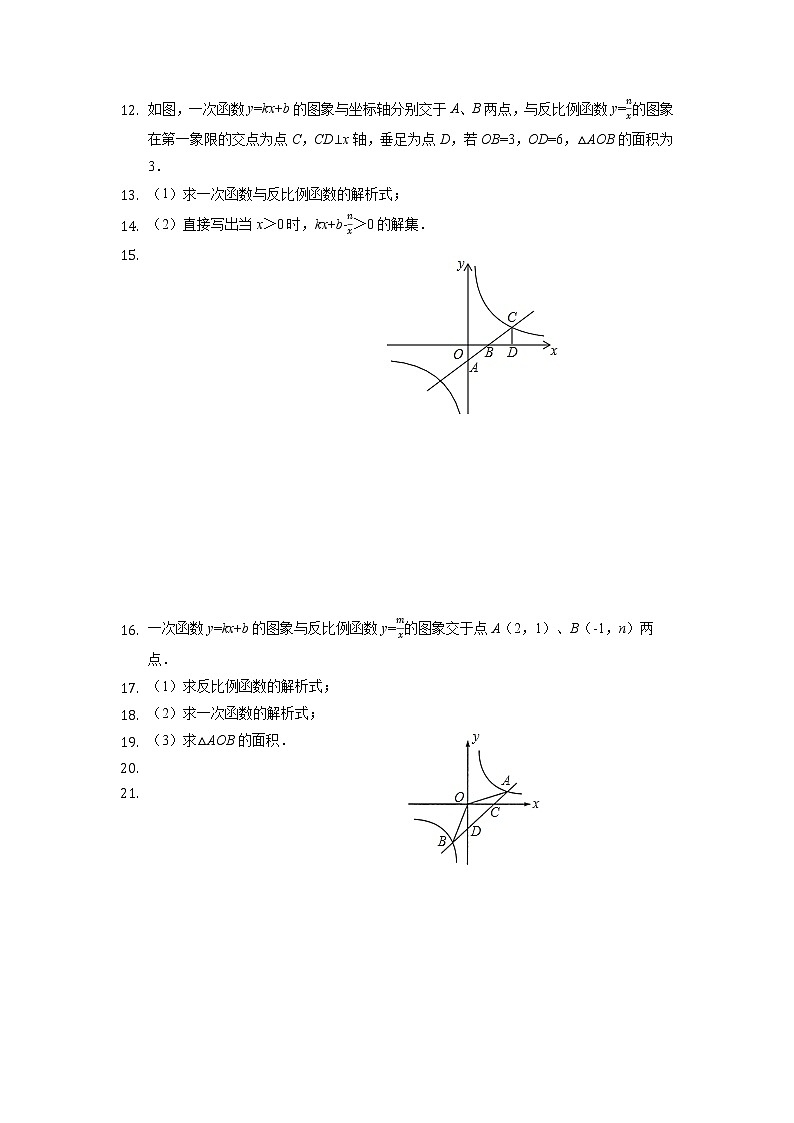
 2022重庆中考数学第二轮复习一次函数和反比例函数综合题专项训练1 已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A（1，4）和点B（m，-2）．（1）求这两个函数的表达式；（2）根据图象直接写出一次函数的值大于反比例函数的值时，x的取值范围．        如图，双曲线y=经过点P（2，1），且与直线y=kx-4（k＜0）有两个不同的交点．（1）求m的值．（2）求k的取值范围．            如图，一次函数y=kx+b的图象与坐标轴分别交于A、B两点，与反比例函数y=的图象在第一象限的交点为点C，CD⊥x轴，垂足为点D，若OB=3，OD=6，△AOB的面积为3．（1）求一次函数与反比例函数的解析式；（2）直接写出当x＞0时，kx+b-＞0的解集．          一次函数y=kx+b的图象与反比例函数y=的图象交于点A（2，1）、B（-1，n）两点．（1）求反比例函数的解析式；（2）求一次函数的解析式；（3）求△AOB的面积．        如图，已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A（1，4）和点B（m，-2），一次函数的图象交x轴于点C．（1）求这两个函数的关系式；（2）求△AOB的面积；
（3）结合图象直接写出y1＞y2时，x的取值范围． 如图，一次函数y=-x+b与反比例函数y=（x> 0）的图象交于点A（m，4）和B（4，1）（1）求b、k、m的值；（2）根据图象直接写出-x+b<（x> 0）的解集；（3）点P是线段AB上一点，过点P作PD⊥x轴于点D，连接OP，若△POD的面积为S，求S的最大值和最小值．         如图，反比例函数y1＝和一次函数y2＝mx+n相交于点A（1，3），B（﹣3，a），（1）求一次函数和反比例函数解析式；（2）连接OA，试问在x轴上是否存在点P，使得△OAP为以OA为腰的等腰三角形，若存在，直接写出满足题意的点P的坐标；若不存在，说明理由．       如图，一次函数的图象与反比例函数的图象交于点A、C两点，其中点，与x轴交于点​​​​​​​求一次函数和反比例函数的表达式；求C点坐标；根据图象，直接写出不等式的解集．         如图，一次函数、为常数，的图象与轴、轴分别交于、两点，且与反比例函数为常数且的图象在第二象限交于点，轴，垂足为，若．求一次函数与反比例函数的解析式；求两个函数图象的另一个交点的坐标；请观察图象，直接写出不等式的解集．       如图，反比例函数y1=的图象与一次函数y2=的图象交于点A，B，点B的横坐标实数4，点P（1，m）在反比例函数y1=的图象上．（1）求反比例函数的表达式；（2）观察图象回答：当x为何范围时，y1＞y2；（3）求△PAB的面积．          如图，直线y=-x+5与双曲线y=（x＞0）相交于A、B两点，与x轴相交于C点，且△BOC的面积是．（1）求反比例函数的表达式及点A的坐标；（2）点E为线段AB上一个动点，且直线OE将△AOB的面积分成1：2的两部分，求点E的坐标．       如图，在直角坐标系xOy中，一直线经过点A（﹣1，0）与y轴正半轴交于B点，在x轴正半轴上有一点D，且OB=OD，过D点作DC⊥x轴交直线y=2x+b于C点，反比例函数（x＞0）经过点C． （1）求b，k的值；（2）求△BDC的面积；（3）在反比例函数（x＞0）的图象上找一点P（异于点C），使△BDP与△BDC的面积相等，求出P点坐标．          如图，一次函数y=kx+b与反比例函数y=（x＞0）的图象交于A（m，6），B（n，3）两点．（1）求一次函数的解析式；（2）根据图象直接写出kx+b-＞0时，x的取值范围；（3）若M是x轴上一点，S△MOB=S△AOB，求点M的坐标．        如图,已知正比例函数y=kx与反比例函数y=的图象在第一象限交于点A(2,4).(1)求正比例函数与反比例函数的表达式;(2)平移直线OA,平移后的直线与x轴交于点B,与反比例函数的图象交于第一象限的点C(4,n).求直线BC的表达式;线段BC的长是          .       如图,直线=-x+4,=x+b都与双曲线y=(x>0)交于点A(1,m),这两条直线分别与x轴交于B,C两点.(1)求k的值;(2)直接写出当x>0时,不等式x+b>的解集;(3)若点P在x轴上,连结AP,且AP把ABC的面积分成1:2两部分,求此时点P的坐标.       如图,已知反比例函数y=(k0)与一次函数y=ax+b相交于点A(n,-1),B(1,3),过点A作ADy轴于点D,过点B作BCx轴于点C,连结CD.(1)求反比例函数的表达式;(2)求四边形ABCD的面积.