

第四章 第1讲 曲线运动 运动的合成与分解—2022高中物理一轮复习学案
展开第1讲 曲线运动 运动的合成与分解
ZHI SHI SHU LI ZI CE GONG GU
知识梳理·自测巩固
知识点1 曲线运动
1.速度方向:质点在某一点的速度方向,沿曲线上该点的切线方向。
2.运动性质:做曲线运动的物体,速度的方向时刻改变,故曲线运动一定是变速运动,即必然具有加速度。
3.曲线运动的条件:
(1)运动学角度:物体的加速度方向跟速度方向不在同一条直线上。
(2)动力学角度:物体所受合外力的方向跟速度方向不在同一条直线上。
思考:当物体的初速度v0和所受的外力F分别满足下列问题中所给定的条件时,物体的运动情况将会是怎样的?
①v0=0,F=0。静止运动
②v0≠0,F=0。匀速直线运动
③v0≠0,F≠0且恒定,两者方向相同。匀加速直线运动
④v0≠0,F≠0且恒定,两者方向相反。匀减速直线运动
⑤v0≠0,F≠0且恒定,两者方向不在一条直线上。匀变速曲线运动
⑥v0≠0,F≠0不恒定且大小、方向都随着时间变化。变速曲线运动。
知识点2 运动的合成与分解
1.分运动和合运动的关系
(1)等时性、独立性、等效性
各分运动与合运动总是同时开始,同时结束。经历的时间一定相等;各分运动是各自独立的,不受其他分运动的影响;各分运动的叠加与合运动具有相同的效果。
(2)合运动的性质是由分运动的性质决定的
2.运动的合成与分解
(1)运动的合成
由几个分运动求合运动。合成的方法是平行四边形定则。
(2)运动的分解
已知合运动求分运动,分解时应根据运动的效果确定两分运动的方向,然后由平行四边形定则确定大小,分解时也可按正交分解法分解,运动的分解与合成是互逆运算。
思考:
如图所示,在军事演习中,飞机常常一边匀加速收拢绳索提升战士,一边沿着水平方向匀速飞行。
(1)战士在水平方向上和竖直方向上分别做什么运动?
(2)战士的合速度的大小、合位移的大小如何计算?
[答案] (1)水平方向做匀速直线,竖直方向做匀加速直线
(2)求出分速度、分位移,再利用平行四边形定则求合速度、合位移。
思维诊断:
(1)曲线运动一定是变速运动。( √ )
(2)曲线运动的速度大小可能不变。( √ )
(3)曲线运动的加速度可以为零。( × )
(4)曲线运动的加速度可以不变。( √ )
(5)合运动不一定是物体的实际运动。( × )
(6)合运动的速度一定大于分运动的速度。( × )
,
1.(2019·江苏黄桥中学模拟)关于物体的受力和运动,下列说法中正确的是( D )
A.物体在不垂直于速度方向的合力作用下,速度大小可能一直不变
B.物体做曲线运动时,某点的加速度方向就是通过这一点曲线的切线方向
C.物体受到变化的合力作用时,它的速度大小一定改变
D.做曲线运动的物体,一定受到与速度不在同一直线上的外力作用
[解析] 本题考查曲线运动的条件。如果合力与速度方向不垂直,必然有沿速度方向的分力,速度大小一定改变,故A错误;物体做曲线运动时,通过某一点的曲线的切线方向是该点的速度方向,而不是加速度方向,比如平抛运动,故B错误;物体受到变化的合力作用时,它的速度大小可以不改变,比如匀速圆周运动,故C错误;物体做曲线运动的条件是一定受到与速度不在同一直线上的外力作用,故D正确。
2.某人骑自行车以4 m/s的速度向正东方向行驶,天气预报报告当时是正北风,风速为4 m/s,那么,骑车人感觉到的风向和风速为( D )
A.西北风 风速为4 m/s B.西北风 风速为4 m/s
C.东北风 风速为4 m/s D.东北风,风速为4 m/s
[解析] 以骑车人为参考系,人向正东方向骑行,感觉风向正西,风速大小为v1=4 m/s,当时有正北风,风速为v2=4 m/s,如图所示,可求得人感觉到的风向为东北风,风速为v=4 m/s,D正确。
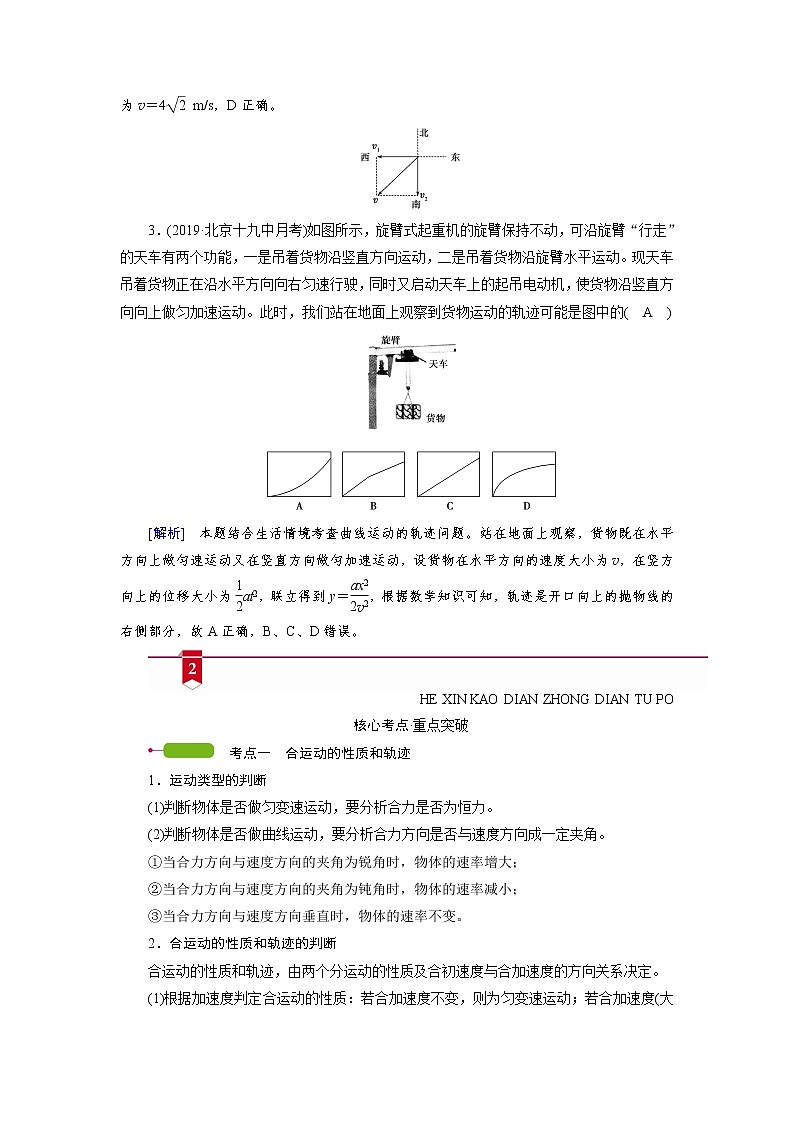
3.(2019·北京十九中月考)如图所示,旋臂式起重机的旋臂保持不动,可沿旋臂“行走”的天车有两个功能,一是吊着货物沿竖直方向运动,二是吊着货物沿旋臂水平运动。现天车吊着货物正在沿水平方向向右匀速行驶,同时又启动天车上的起吊电动机,使货物沿竖直方向向上做匀加速运动。此时,我们站在地面上观察到货物运动的轨迹可能是图中的( A )
[解析] 本题结合生活情境考查曲线运动的轨迹问题。站在地面上观察,货物既在水平方向上做匀速运动又在竖直方向做匀加速运动,设货物在水平方向的速度大小为v,在竖方向上的位移大小为at2,联立得到y=,根据数学知识可知,轨迹是开口向上的抛物线的右侧部分,故A正确,B、C、D错误。
HE XIN KAO DIAN ZHONG DIAN TU PO
核心考点·重点突破
考点一 合运动的性质和轨迹
1.运动类型的判断
(1)判断物体是否做匀变速运动,要分析合力是否为恒力。
(2)判断物体是否做曲线运动,要分析合力方向是否与速度方向成一定夹角。
①当合力方向与速度方向的夹角为锐角时,物体的速率增大;
②当合力方向与速度方向的夹角为钝角时,物体的速率减小;
③当合力方向与速度方向垂直时,物体的速率不变。
2.合运动的性质和轨迹的判断
合运动的性质和轨迹,由两个分运动的性质及合初速度与合加速度的方向关系决定。
(1)根据加速度判定合运动的性质:若合加速度不变,则为匀变速运动;若合加速度(大小或方向)变化,则为非匀变速运动。
(2)根据合加速度的方向与合初速度的方向判定合运动的轨迹:若合加速度的方向与合初速度的方向在同一直线上则为直线运动,否则为曲线运动。
(3)合力(或合加速度)方向与轨迹的关系
物体做曲线运动的轨迹一定夹在合力(或合加速度)方向和速度方向之间,速度方向与轨迹相切,合力(或合加速度)方向指向曲线的凹侧。
例1 (多选)如图所示的直角三角板紧贴在固定的刻度尺上方,若使三角板沿刻度尺向右匀速运动的同时,一支铅笔从三角板直角边的最下端,由静止开始沿此边向上做匀加速直线运动,下列关于铅笔尖的运动及其留下的痕迹的判断,其中正确的有( AD )
A.笔尖留下的痕迹是一条抛物线
B.笔尖留下的痕迹是一条倾斜的直线
C.在运动过程中,笔尖的速度方向始终保持不变
D.在运动过程中,笔尖的加速度方向始终保持不变
[解析] 笔尖水平方向是匀速直线运动,竖直方向是初速度为零的匀加速直线运动,故笔尖做匀变速曲线运动,其轨迹是抛物线,A、D正确。
规律总结:
两个直线运动的合运动性质的判断
根据合加速度方向与合初速度方向判定合运动是直线运动还是曲线运动,具体分以下几种情况:
两个互成角度的分运动 | 合运动的性质 |
两个匀速直线运动 | 匀速直线运动 |
一个匀速直线运动、一个匀变速直线运动 | 匀变速曲线运动 |
两个初速度为零的匀加速直线运动 | 匀加速直线运动 |
两个初速度不为零 的匀变速直线运动 | 如果v合与a合共线,为匀变速直线运动 |
如果v合与a合不共线,为匀变速曲线运动 |
〔类题演练1〕
(2019·浙江月考)如图所示,一物块仅在三个共点恒力F1、F2、F3的作用下以速度v0水平向右做匀速直线运动,其中F1斜向右上方,F2竖直向下,F3水平向左。某时刻撤去其中的一个力,其他力的大小和方向不变,一段时间后恢复该力,则下列说法不正确的是( D )
A.如果撤去的是F1,则物块先做匀变速曲线运动,恢复该力之后将做直线运动
B.如果撤去的是F1,恢复F1时物块的速度大小可能为v0
C.如果撤去的是F3,物块将向右做匀加速直线运动,恢复该力之后做匀速直线运动
D.如果撤去的是F2,在恢复该力之前的时间内,因物块做曲线运动,故在相等时间间隔内其速度的变化量Δv的方向时刻在改变
[解析] A项,物块在三个共点力F1、F2、F3的作用下以速度v0水平向右做匀速直线运动,说明三个共点力平衡,如果撤去F1,则F2、F3的合力与F1等大反向,合力与初速度不在一条直线上,物块做匀变速曲线运动,恢复F1,物块又处于平衡状态,做匀速直线运动,故A项正确;B项,撤去F1,F2、F3的合力对物块可能先做负功后做正功,有可能总功为零,即恢复F1时物块的速度大小可能为v0,故B项正确;C项,撤去F3后,合力水平向右,故物块向右做匀加速直线运动,恢复该力之后做匀速直线运动,故C项正确;D项,撤去F2之后,物块做类平抛运动,则Δv=aΔt,因为加速度a是恒定的矢量,故在相等时间间隔内Δv的大小和方向都不变,故D项错误。
考点二 运动的合成与分解的应用
1.合运动和分运动的关系
(1)等时性:各个分运动与合运动总是同时开始,同时结束,经历时间相等(不同时的运动不能合成)。
(2)独立性:一个物体同时参与几个分运动时,各分运动独立进行,互不影响。
(3)等效性:各分运动叠加起来与合运动有完全相同的效果。
(4)同一性:各分运动与合运动是指同一物体参与的分运动和实际发生的运动,不能是几个不同物体发生的不同运动。
2.运动的合成与分解的运算法则
运动的合成与分解是指描述运动的各物理量即位移、速度、加速度的合成与分解,由于它们均是矢量,故合成与分解都遵守平行四边形定则。
例2 (2020·河北邯郸模拟)质量为2 kg的质点在直角坐标系xOy平面内做曲线运动,在x轴方向的速度—时间图象和y轴方向的位移—时间图象分别如图甲、乙所示,下列说法正确的是( B )
A.质点的初速度大小为3 m/s
B.质点所受的合外力大小为3 N
C.质点初速度的方向与合外力方向垂直
D.2 s末质点速度大小为6 m/s
[解析] 本题借助v-t图象和s-t图象分析运动的合成问题。当t=0时通过图甲可以看出质点在x轴方向的分运动为匀加速直线运动,初速度为vx=3 m/s,通过图乙可以看出质点在y轴方向的分运动为匀速直线运动,速度大小为vy=4 m/s,因此质点的初速度为v0==5 m/s,故A错误,质点在y轴方向上做匀速运动,所受合力为零,在x轴方向加速度为ax== m/s2=1.5 m/s2,由牛顿第二定律可知质点在x轴方向所受合力为Fx=max=3 N,所以质点所受合外力为3 N,故B正确;质点初速度方向与x轴方向成锐角,与合外力方向不垂直,故C错误;在2 s末质点在x轴方向分速度为6 m/s,y轴方向分速度为4 m/s,合速度为2 m/s,故D错误。
考点三 绳、杆上速度的分解(牵连速度问题)
解决绳、杆上速度的分解问题,非常重要的一点是清楚绳或杆的特点:(1)不计质量;(2)不可伸长;(3)沿绳(或杆)方向的速度分量大小相等。
解题的一般思路与方法:
合运动→绳拉物体的实际运动速度v
分运动→
方法:v1与v2的合成遵循平行四边形定则。
常见的模型如图所示。
例3 人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度v0匀速地拉绳,使物体A到达如图所示位置时,绳与竖直杆的夹角为θ,则物体A实际运动的速度为( D )
A.v0sin θ B.
C.v0cos θ D.
[解析] 由运动的合成与分解可知,物体A参与两个分运动:一个是沿着它相连接的绳子的运动,另一个是垂直于绳子斜向上的运动,而物体A的实际运动轨迹是沿着竖直杆向上的,这一轨迹所对应的运动就是物体A的合运动,它们之间的关系如图所示。由几何关系可得v=,所以D项正确。
〔类题演练2〕
如图所示,一根长为L的轻杆OA,O端用铰链固定在水平面上,轻杆靠在一个高为h的物块上,某时刻杆与水平方向的夹角为θ,物块水平向右运动的速度为v,则此时A点速度为( C )
A. B.
C. D.
[解析] 根据运动的效果可将物块水平向右运动的速度,沿垂直于杆和沿平行于杆的方向分解成v2和v1,根据平行四边形定则可得v1=vcos θ,v2=vsin θ,根据几何关系可得OB=,由于B点的线速度为v2=vsin θ=OBω,所以ω==,所以A点的线速度vA=Lω=,C正确。
JIE DUAN PEI YOU CHA QUE BU LOU
阶段培优·查缺补漏
“小船渡河”模型
一条宽为L的河流,水流的速度为v1,船在静水中的速度为v2,船从河的一边渡到对岸。船过河的过程同时参与了两种运动,即船相对于水的运动和随水流的运动,船的实际运动为合运动。船在静水中的速度v2方向取决于船头朝向,船的实际运动方向取决于合速度方向。
1.船过河的最短时间
如图甲所示,设船头斜向上游与河岸成θ角,船在垂直于河岸方向的速度为:v⊥=v2sin θ,渡河所需时间为:t==,当θ=90°时,t最小。所以当船头垂直于河岸渡河时,渡河所需时间最短,最短时间为t=。
2.船过河的最短航程
(1)当v2>v1时,如图乙所示,为了使船过河的航程最短,必须使船的合速度v方向与河岸垂直,则船头指向上游,与河岸成一定的角度θ,cos θ=。由于0<cos θ<1,因此只有在v2>v1时,船才可以垂直河岸过河。所以当v2>v1时,船头与上游河岸成θ=arccos的角,船过河的航程最短,最短航程为L。
(2)当v2<v1时,不论船头方向如何,船都会被冲向下游,不可能垂直河岸过河。如图丙所示,设船头与上游河岸成θ角,合速度与下游河岸成α角。由图可知:α角越大,航程越短。以v1的矢尖为圆心、以v2的大小为半径画圆,当v与圆相切时,α角最大,此时cos θ=。所以当v2<v1时,船头与上游河岸成θ=arccos的角,船过河的最短航程为:=L。
(3)当v2=v1时,最短航程趋近于L。
例4 一小船渡河,河宽d=180 m,水流速度v1=2.5 m/s。
(1)若船在静水中的速度为v2=5 m/s,求:
①欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?
②欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
(2)若船在静水中的速度v2=1.5 m/s,要使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
[解析] (1)若v2=5 m/s
①欲使船在最短时间内渡河,船头应朝垂直河岸方向。
当船头垂直河岸时,如图所示,合速度为倾斜方向,垂直分速度为v2=5 m/s。t== s=36 s
v合== m/s
s合=v合t=90 m
②欲使船渡河航程最短,合运动应垂直
河岸,船头应朝上游,与上游河岸方向夹角为α
垂直河岸过河就要求v水平=0,如图所示,有v2cos α=v1得α=60°,所以当船头与上游河岸夹角为60°时航程最短。
s=d=180 m
t===s=24s。
(2)若v2=1.5 m/s,与(1)中②不同,因为船速小于水速,所以船一定向下游漂移,设合速度方向与河岸下游方向夹角为α,则航程s=。欲使航程最短,需α最大,如图所示,由出发点A作出v1矢量,以v1矢量末端为圆心,v2大小为半径作圆,A点与圆周上某点的连线即为合速度方向,欲使v合与水平方向夹角最大,应使v合与圆相切,即v合⊥v2。
sin α===,解得α=37°。
所以船头与上游河岸夹角为90°-37°=53°
t=== s=150 s
v合=v1cos 37°=2 m/s
s=v合·t=300 m
[答案] (1)①垂直河岸方向 36 s 90 m
②与上游河岸夹角为60° 24 s 180 m
(2)与上游河岸夹角为53° 150 s 300 m
〔类题演练3〕
(2020·山东潍坊模拟)河宽d,一小船从A岸到B岸。已知船在静水中的速度v大小不变,航行中船头始终垂直河岸,水流的速度方向与河岸平行,若小船的运动轨迹如图所示,则( B )
A.越接近河岸船的速度越大
B.越接近河岸水的流速越小
C.各处水的流速相同
D.船渡河所用的时间小于
[解析] 从轨迹曲线的弯曲形状上可以知道,小船先具有向下游的加速度,后具有向上游的加速度,故水流是先加速后减速,即越接近河岸水流速度越小,而船的速度v船=,越接近河岸船的速度越小,故A、C错误B正确;由于船身方向垂直于河岸,无论水流速度是否变化,这种渡河方式耗时最短,即为,故D错误。
2 NIAN GAO KAO MO NI XUN LIAN
2年高考·模拟训练
1.(2018·北京理综,20)根据高中所学知识可知,做自由落体运动的小球,将落在正下方位置。但实际上,赤道上方200 m处无初速下落的小球将落在正下方位置偏东约6 cm处。这一现象可解释为,除重力外,由于地球自转,下落过程小球还受到一个水平向东的“力”,该“力”与竖直方向的速度大小成正比。现将小球从赤道地面竖直上抛,考虑对称性,上升过程该“力”水平向西,则小球( D )
A.到最高点时,水平方向的加速度和速度均为零
B.到最高点时,水平方向的加速度和速度均不为零
C.落地点在抛出点东侧
D.落地点在抛出点西侧
[解析] A错:将小球竖直上抛的运动分解为水平和竖直两个分运动。上升阶段,随着小球竖直分速度的减小,其水平向西的力逐渐变小,因此水平向西的分加速度逐渐变小,小球的水平分运动是向西的变加速运动,故小球到最高点时水平向西的速度达到最大值,在最高点速度不为零。
B错:小球到最高点时竖直方向的分速度为零,由题意知小球这时不受水平方向的力,故小球到最高点时水平分加速度为零。
C错、D对:下降阶段,随着小球竖直分速度的变大,其水平向东的力逐渐变大,水平向东的分加速度逐渐变大,小球的水平分运动是向西的变减速运动,故小球的落地点应在抛出点的西侧。
2.(2018·江苏单科,3)某弹射管每次弹出的小球速度相等。在沿光滑竖直轨道自由下落过程中,该弹射管保持水平,先后弹出两只小球。忽略空气阻力,两只小球落到水平地面的( B )
A.时刻相同,地点相同 B.时刻相同,地点不同
C.时刻不同,地点相同 D.时刻不同,地点不同
[解析] 弹出的小球做平抛运动,竖直方向的分运动为自由落体运动,水平方向的分运动为匀速直线运动。弹射管自由下落,两只小球始终处于同一水平面,因此两只小球同时落地。由h=gt2知,两只小球在空中运动的时间不相等,由x=vt知水平位移不相等,落地点不同。
3.(2019·四川成都石室中学一诊)一条小船在静水中的速度为3 m/s,它要渡过一条宽为60 m的长直河道,河水流速为4 m/s,则( D )
A.这条船不可能渡过这条河
B.这条船过河时间可能为15 s
C.这条船可以渡过这条河,而且过河时的合速度可以为 9 m/s
D.这条船能够过河的最小位移为80 m
[解析] 本题考查小船渡河问题。当船在垂直于河岸方向有分速度,船就能渡过河,故A错误;当船头与河岸垂直时,渡河时间最短,最短时间tmin== s=20 s,可知小船过河时间不可能为15 s,故B错误;当船头与河岸方向平行时,合速度最大为7 m/s,小于9 m/s,故C错误;当船头与合速度方向垂直时,船的位移最小,设合速度与河岸间的夹角为θ,则sin θ==,x=80 m,故D正确。
4.(2019·陕西宝鸡二模)如图所示的机械装置可以将圆周运动转化为直线上的往复运动。连杆AB、OB可绕图中A、B、O三处的转轴转动,连杆OB在竖直面内的圆周运动可通过连杆AB使滑块在水平横杆上左右滑动。已知OB杆长为L,绕O点沿逆时针方向匀速转动且角速度为ω,当连杆AB与水平方向夹角为α,AB杆与OB杆的夹角为β时,滑块的水平速度大小为( D )
A. B.
C. D.
[解析] 本题借助杆模型考查运动的合成与分解。设滑块的速度大小为v,A点的速度的方向沿水平方向,
如图将A点的速度进行分解,根据运动的合成与分解可知,A点在沿杆AB方向的分速度为vA分=vcos α,B点做圆周运动,实际速度是圆周运动的线速度,可以分解为沿杆方向的分速度和垂直于杆方向的分速度,如图设B的线速度为v′,设v′与杆AB夹角为θ,由几何知识可知θ=β-,则vB分=v′·cos θ=v′cos(90°-β)=v′sin β,v′=ωL,二者沿杆AB方向的分速度是相等的,即vA分=vB分,联立可得v=,故D正确。
备考2024届高考物理一轮复习讲义第四章曲线运动第1讲曲线运动运动的合成与分解考点2运动的合成与分解: 这是一份备考2024届高考物理一轮复习讲义第四章曲线运动第1讲曲线运动运动的合成与分解考点2运动的合成与分解,共4页。
备考2024届高考物理一轮复习讲义第四章曲线运动第1讲曲线运动运动的合成与分解考点1曲线运动中力和运动的关系: 这是一份备考2024届高考物理一轮复习讲义第四章曲线运动第1讲曲线运动运动的合成与分解考点1曲线运动中力和运动的关系,共4页。
高中物理高考 第1讲 曲线运动 运动的合成与分解: 这是一份高中物理高考 第1讲 曲线运动 运动的合成与分解,共30页。学案主要包含了堵点疏通,对点激活等内容,欢迎下载使用。












