专题15 二次函数中的圆和直线相切问题-2021-2022学年九年级数学上册难点突破（人教版）

这是一份专题15 二次函数中的圆和直线相切问题-2021-2022学年九年级数学上册难点突破（人教版），文件包含专题15二次函数中的圆和直线相切问题解析版docx、专题15二次函数中的圆和直线相切问题原卷版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
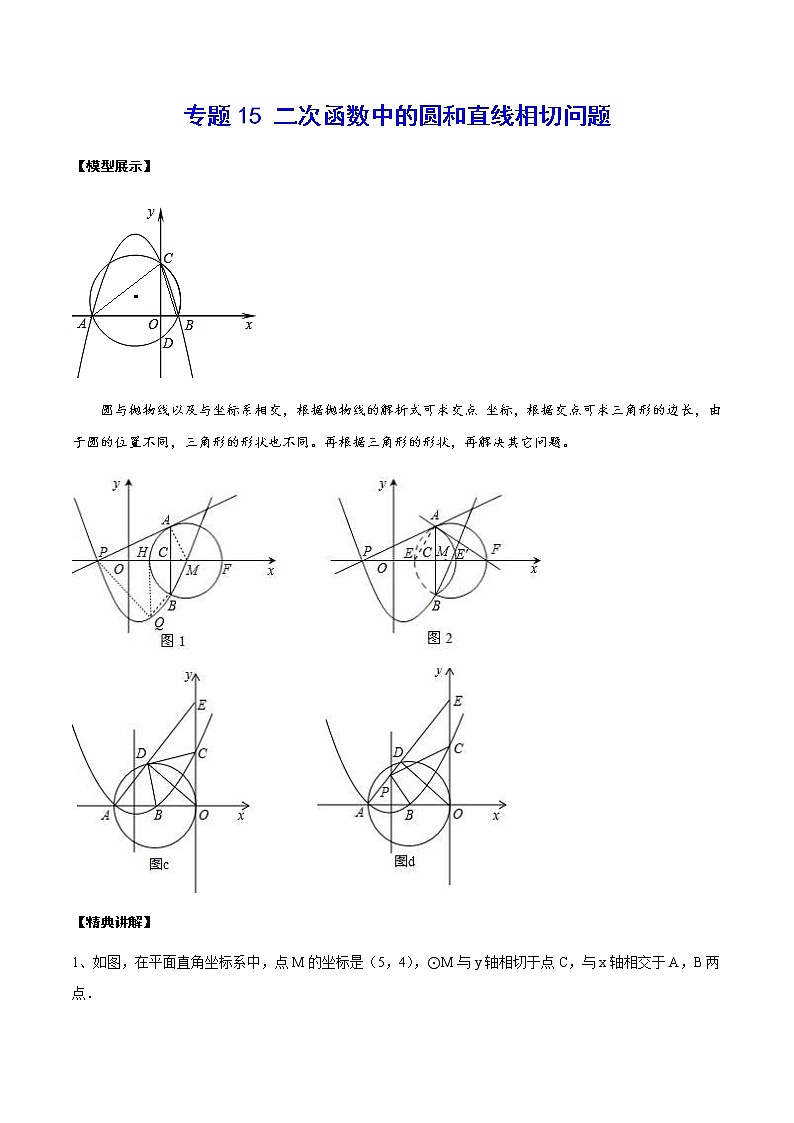
专题15 二次函数中的圆和直线相切问题【模型展示】圆与抛物线以及与坐标系相交，根据抛物线的解析式可求交点 坐标，根据交点可求三角形的边长，由于圆的位置不同，三角形的形状也不同。再根据三角形的形状，再解决其它问题。【精典讲解】1、如图，在平面直角坐标系中，点M的坐标是（5，4），⊙M与y轴相切于点C，与x轴相交于A，B两点．（1）则点A，B，C的坐标分别是A （2，0） ，B （8，0） ，C  （0，4） ；（2）设经过A，B两点的抛物线解析式为y=（x-5）2+k，它的顶点为E，求证：直线EA与⊙M相切；（3）在抛物线的对称轴上，是否存在点P，且点P在x轴的上方，使△PBC是等腰三角形？如果存在，请求出点P的坐标；如果不存在，请说明理由．    2、如图，已知抛物线y=-（x2-7x+6）的顶点坐标为M，与x轴相交于A，B两点（点B在点A的右侧），与y轴相交于点C．（1）用配方法将抛物线的解析式化为顶点式：y=a（x-h）2+k（a≠0），并指出顶点M的坐标；（2）在抛物线的对称轴上找点R，使得CR+AR的值最小，并求出其最小值和点R的坐标；（3）以AB为直径作⊙N交抛物线于点P（点P在对称轴的左侧），求证：直线MP是⊙N的切线． 3、已知二次函数y＝－x2＋bx＋c＋1.(1)当b＝1时，求这个二次函数的对称轴的方程；(2)若c＝－b2－2b，问：b为何值时，二次函数的图象与x轴相切；(3)如图所示，若二次函数的图象与x轴交于点A(x1，0)，B(x2，0)，且x1＜x2，与y轴的正半轴交于点M，以AB为直径的半圆恰好经过点M，二次函数的对称轴l与x轴，直线BM，直线AM分别相交于点D，E，F，且满足＝，求二次函数的表达式． 4、如图所示，已知抛物线y＝ax2＋bx＋c(a≠0)的图象的顶点坐标是(2，1)，并且经过点(4，2)．直线y＝x＋1与抛物线交于B，D两点，以BD为直径作圆，圆心为点C，⊙C与直线m交于对称轴右侧的点M(t，1)．直线m上每一点的纵坐标都等于1.(1)求抛物线的表达式；(2)证明：⊙C与x轴相切；(3)过点B作BE⊥m，垂足为E，再过点D作DF⊥m，垂足为F.求BE∶MF的值． 5、已知抛物线y＝x2＋mx－2m－4(m>0)．(1)证明：该抛物线与x轴总有两个不同的交点．(2)设该抛物线与x轴的两个交点分别为A，B(点A在点B的右侧)，与y轴交于点C，A，B，C三点都在⊙P上．①试判断：不论m取任何正数，⊙P是否经过y轴上某个定点？若是，求出该定点的坐标；若不是，说明理由；②若点C关于直线x＝－的对称点为点E，点D(0，1)，连结BE，BD，DE，△BDE的周长记为l，⊙P的半径记为r，求的值．设BD＝a，BE＝2a，则DE＝a，∴＝＝.   6、在平面直角坐标系中，二次函数y＝ax2＋x＋c的图象经过点C(0，2)和点D(4，－2)，点E是直线y＝－x＋2与二次函数图象在第一象限内的交点．(1)求二次函数的表达式及点E的坐标；(2)如图1，若点M是二次函数图象上的点，且在直线CE的上方，连结MC，OE，ME，求四边形COEM面积的最大值及此时点M的坐标；(3)如图2，经过A，B，C三点的圆交y轴于点F，求点F的坐标．7、若抛物线L：y=ax2+bx+c（a，b，c是常数，abc≠0）与直线l都经过y轴上的同一点，且抛物线L的顶点在直线l上，则称次抛物线L与直线l具有“一带一路”关系，并且将直线l叫做抛物线L的“路线”，抛物线L叫做直线l的“带线”．（1）若“路线”l的表达式为y=2x﹣4，它的“带线”L的顶点的横坐标为﹣1，求“带线”L的表达式；（2）如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系，求m，n的值；（3）设（2）中的“带线”L与它的“路线”l在y轴上的交点为A．已知点P为“带线”L上的点，当以点P为圆心的圆与“路线”l相切于点A时，求出点P的坐标．8、如图①已知抛物线y=ax2﹣3ax﹣4a（a＜0）的图象与x轴交于A、B两点（A在B的左侧），与y的正半轴交于点C，连结BC，二次函数的对称轴与x轴的交点为E．（1）抛物线的对称轴与x轴的交点E坐标为_____，点A的坐标为_____；（2）若以E为圆心的圆与y轴和直线BC都相切，试求出抛物线的解析式；（3）在（2）的条件下，如图②Q（m，0）是x的正半轴上一点，过点Q作y轴的平行线，与直线BC交于点M，与抛物线交于点N，连结CN，将△CMN沿CN翻折，M的对应点为M′．在图②中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．9、如图，在平面直角坐标系xOy中，经过C（1，1）的抛物线y＝ax2+bx+c（a＞0）顶点为M，与x轴正半轴交于A，B两点．（1）如图1，连接OC，将线段OC绕点O逆时针旋转使得C落在y轴的正半轴上，求线段OC过的面积；（2）如图2，延长线段OC至N，使得ON＝OC，若∠ONA＝∠OBN且tan∠BAM＝，求抛物线的解析式；（3）如图3，已知以直线x＝为对称轴的抛物线y＝ax2+bx+c交y轴于（0，5），交直线l：y＝kx+m（k＞0）于C，D两点，若在x轴上有且仅有一点P，使∠CPD＝90°，求k的值．10、如图1，抛物线与y轴交于点C，与x轴交于点A、B（点A在点B左边），O为坐标原点．点D是直线BC上方抛物线上的一个动点，过点D作DE∥x轴交直线BC于点E．点P为∠CAB角平分线上的一动点，过点P作PQ⊥BC于点H，交x轴于点Q；点F是直线BC上的一个动点．（1）当线段DE的长度最大时，求DF+FQ+PQ的最小值．（2）如图2，将△BOC沿BC边所在直线翻折，得到△BOC′，点M为直线BO′上一动点，将△AOC绕点O顺时针旋转α度（0°＜α＜180°）得到△A′OC′，当直线A′C′，直线BO′，直线OM围成的图形是等腰直角三角形时，直接写出该等腰直角三角形的面积．11、如图，抛物线y＝﹣x2+bx+c与x轴交于A、B（A左B右），与y轴交于C，直线y＝﹣x+5经过点B、C．（1）求抛物线的解析式；（2）点P为第二象限抛物线上一点，设点P横坐标为m，点P到直线BC的距离为d，求d与m的函数解析式；（3）在（2）的条件下，若∠PCB+∠POB＝180°，求d的值．12、在平面直角坐标系中，对“隔离直线”给出如下定义：点是图形上的任意一点，点是图形上的任意一点，若存在直线：满足且，则称直线：是图形与的“隔离直线”，如图，直线：是函数的图像与正方形的一条“隔离直线”.
 （1）在直线①，②，③，④中，是图函数的图像与正方形的“隔离直线”的为          .（2）如图，第一象限的等腰直角三角形的两腰分别与坐标轴平行，直角顶点的坐标是，⊙O的半径为，是否存在与⊙O的“隔离直线”？若存在，求出此“隔离直线”的表达式：若不存在，请说明理由；（3）正方形的一边在轴上，其它三边都在轴的左侧，点是此正方形的中心，若存在直线是函数的图像与正方形的“隔离直线”，请直接写出的取值范围.13、如图，已知直角坐标平面上的，，，且，，．若抛物线经过、两点．求、的值；将抛物线向上平移若干个单位得到的新抛物线恰好经过点，求新抛物线的解析式；设中的新抛物的顶点点，为新抛物线上点至点之间的一点，以点为圆心画图，当与轴和直线都相切时，联结、，求四边形的面积．14、如图，在直角坐标系中，直线y=﹣x﹣1与x轴，y轴的交点分别为A、B，以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C，直线x=﹣1与x轴交于点D．（1）求抛物线的解析式；（2）在线段AB上是否存在一点P，使以A，D，P为顶点的三角形与△AOB相似？若存在，求出点P的坐标；如果不存在，请说明理由；（3）若点Q在第三象限内，且tan∠AQD=2，线段CQ是否存在最小值，如果存在直接写出最小值；如果不存在，请说明理由．15、如图，抛物线y＝ax2+bx+6与x轴交于点A（6，0），B（﹣1，0），与y轴交于点C．（1）求抛物线的解析式；（2）若点M为该抛物线对称轴上一点，当CM+BM最小时，求点M的坐标．（3）抛物线上是否存在点P，使△BCP为等腰三角形？若存在，有几个？并请在图中画出所有符合条件的点P，（保留作图痕迹）；若不存在，说明理由．