初中数学苏科版九年级下册第7章 锐角函数综合与测试单元测试课后作业题

《第7章 锐角三角函数》单元练习

一．选择题

1．在一个直角三角形中，如果三角形各边的长度都扩大3倍，那么这个三角形的两个锐角的余弦值（　　）

A．都没有变化 B．都扩大3倍 

C．都缩小为原来的 D．不能确定是否发生变化

2. 在Rt△ABC中，∠C = 90°，若sin A=，BC =4，则AB的长是（   ）

A.   6     B.     C.      D.

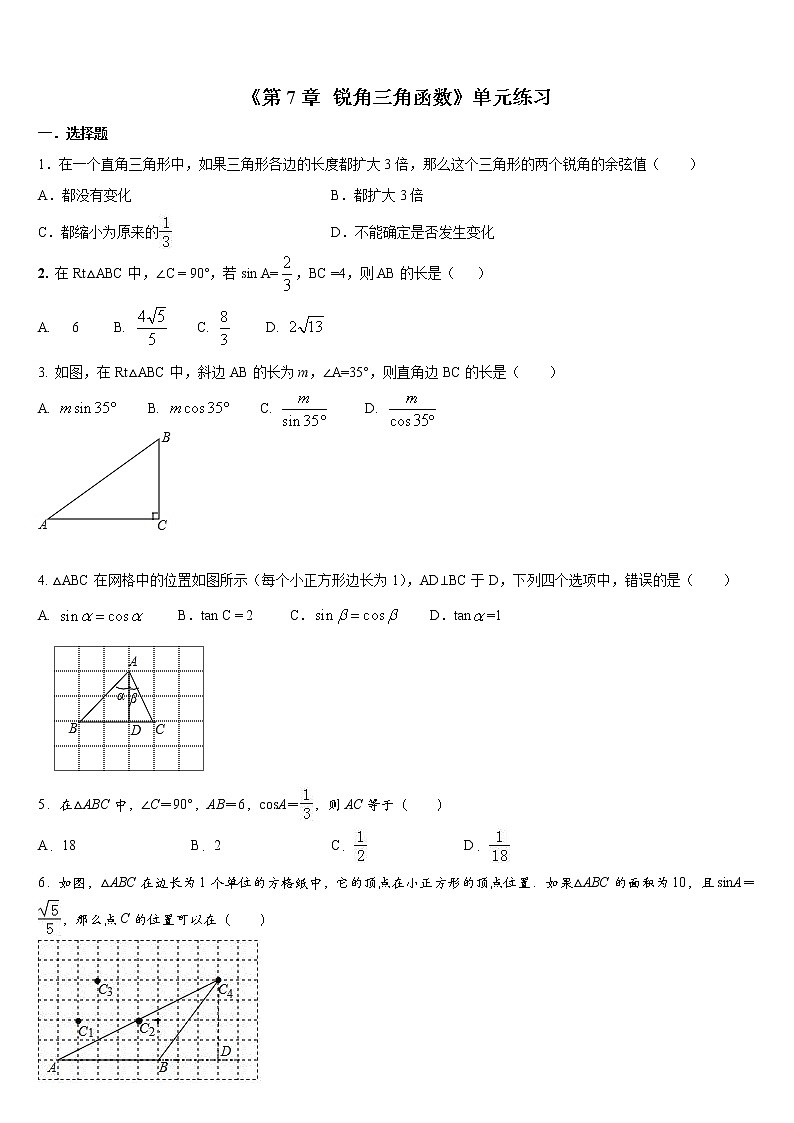
3. 如图，在Rt△ABC中，斜边AB的长为m，∠A=35°，则直角边BC的长是（　　）

A.     B.     C.      D.

4. △ABC在网格中的位置如图所示（每个小正方形边长为1），AD⊥BC于D，下列四个选项中，错误的是（　　）

A.      B．tan C = 2     C．     D．tan=1

5．在△ABC中，∠C＝90°，AB＝6，cosA＝，则AC等于（　　）

A．18 B．2 C． D．

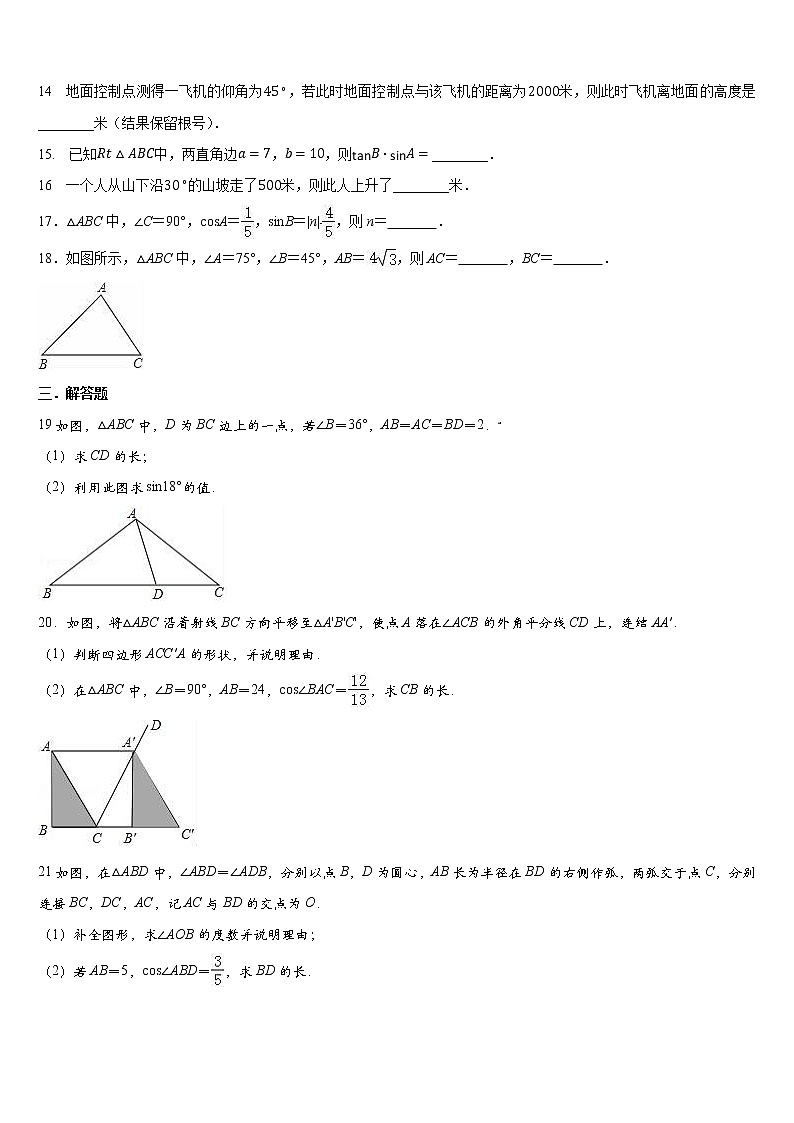
6．如图，△ABC在边长为1个单位的方格纸中，它的顶点在小正方形的顶点位置．如果△ABC的面积为10，且sinA＝，那么点C的位置可以在（　　）

A．点C1处 B．点C2处 C．点C3处 D．点C4处

7．如图，一块三角形空地上种草皮绿化，已知AB＝20米，AC＝30米，∠A＝150°，草皮的售价为a元/米2，则购买草皮至少需要（　　）

A．450a元 B．225a元 C．150a元 D．300a元

8．已知sinα＝，求α，若用计算器计算且结果为“30”，最后按键（　　）

A．AC10N B．SHIET C．MODE D．SHIFT

9．一个三角形的一边是2m，这边上的中线为m，另两边之和为m+m，则这个三角形的面积是（　　）

A．m2 B． m2 C． m2 D．3m2

10．水库大坝横断面是梯形ABCD，坝顶宽AD＝6m，坝高DE＝24m，斜坡AB的坡角是45°，斜坡CD的坡比i＝1：2，则坝底BC的长是（　　）m．

A．30+8 B．30+24 C．42 D．78

二．填空题

11．如图，B、C是河岸边两点，A是对岸岸边一点，测得∠ABC＝45°，∠ACB＝45°，BC＝60 m，则点A到对岸BC的距离是　   　m．

12.  如图，在 中， ， ，，则 ________.

 

13．若△ABC中，∠C＝90°，则是∠A的　   　函数．

14  地面控制点测得一飞机的仰角为，若此时地面控制点与该飞机的距离为米，则此时飞机离地面的高度是________米（结果保留根号）．  

15.  已知中，两直角边，，则________．  

16  一个人从山下沿的山坡走了米，则此人上升了________米．

17．△ABC中，∠C＝90°，cosA＝，sinB＝|n|﹣，则n＝　   　．

18．如图所示，△ABC中，∠A＝75°，∠B＝45°，AB＝，则AC＝　   　，BC＝　   　．

三．解答题

19如图，△ABC中，D为BC边上的一点，若∠B＝36°，AB＝AC＝BD＝2．

（1）求CD的长；

（2）利用此图求sin18°的值．

20．如图，将△ABC沿着射线BC方向平移至△A'B'C'，使点A落在∠ACB的外角平分线CD上，连结AA′．

（1）判断四边形ACC′A的形状，并说明理由．

（2）在△ABC中，∠B＝90°，AB＝24，cos∠BAC＝，求CB的长．

21如图，在△ABD中，∠ABD＝∠ADB，分别以点B，D为圆心，AB长为半径在BD的右侧作弧，两弧交于点C，分别连接BC，DC，AC，记AC与BD的交点为O．

（1）补全图形，求∠AOB的度数并说明理由；

（2）若AB＝5，cos∠ABD＝，求BD的长．

22如图，小华家的住宅楼AB与北京奥运会主体育场鸟巢隔水相望且能看到鸟巢的最高处CD，两建筑物的底部在同一水平面上，视野开阔，但不能直接到达，小华为了测量鸟巢的最大高度CD，只能利用所在住宅楼的地理位置．现在小华仅有的测量工具是皮尺和测角仪（皮尺可测量长度，测角仪可测量仰角、俯角），请你帮助小华设计一个测量鸟巢的最大高度的方案．

（1）要求写出测量步骤和必需的测量数据（用字母表示）并画出测量图形（测角仪高度忽略不计）；

（2）利用小华测量的数据（用字母表示），写出计算鸟巢最大高度CD的表达式．

23．如图，点A、B为地球仪的南、北极点，直线AB与放置地球仪的平面交于点D，所成的角度约为67°，半径OC所在的直线与放置平面垂直，垂足为点E．DE＝15cm，AD＝14cm．求半径OA的长．（精确到0.1cm） （参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）

24．某太阳能热水器的横截面示意图如图所示，已知真空热水管AB与支架CD所在直线相交于点O，且OB＝OD，支架CD与水平线AE垂直，∠BAC＝30°，∠CDE＝45°，DE＝80cm，AC＝180cm．

（1）求支架CD的长；

（2）求真空热水管AB的长．（结果保留根号）

参考答案与试题解析

1. A  2. A  3.A  4. C 5.D 6.D 7.B 8. D 9. B 10. D

11．30米．

12.

13.

14.

15．解：△ABC中，∠C＝90°，是∠A的对边与邻边的比值，

∴是∠A的正切函数．

16．解：在△ABC中，∠C＝90°，

∴∠A+∠B＝90°，

∴sinB＝cosA，

∴|n|﹣＝，

∴|n|＝1，

∴n＝±1．

故答案为±1．

17．解：作AE⊥BC于E点．

在Rt△ABE中，∠B＝45°，

则△ABC为等腰直角三角形，

∴AE＝BE＝；

在Rt△ACE中，

可得∠CAE＝30°，

则CE＝tan30°×AB＝，

AC＝＝，

故BC＝BE+CE＝．

18．解：设直角△ABC中，∠C＝90°，AB＝c＝13cm，BC＝a，AC＝b，

设a＜b，较小锐角α就是∠A，

根据条件可得：，解得：，

∴锐角α的各三角函数值分别是：sinα＝，cosα＝，tanα＝，cotα＝．

19【答案】

增大．

【解答】

解：（1）∵   ，
∴   和均为直角三角形．
∴   ，．
∴   ．

（2）由（1）可知锐角的正切函数值随角度的增大而增大．
 

20．解：（1）四边形ACC'A'是菱形．理由如下：

由平移的性质得到：AC∥A′C′，且AC＝A′C′，

则四边形ACC'A'是平行四边形．

又∵CD平分∠ACB的外角，

∴∠ACA′＝∠A'CC'，

∵AA'∥BB'，

∴∠C'CA'＝∠AA'C，

∴∠AA'C＝∠ACA'，

∴AA'＝AC，

∴四边形ACC'A'是菱形．

（2）∵在△ABC中，∠B＝90°，AB＝24，cos∠BAC＝，

∴cos∠BAC＝＝，即＝，

∴AC＝26．

∴由勾股定理知：BC＝＝＝10．

21．解：（1）补全的图形，如图所示，可得出∠AOB＝90°，理由如下：

证明：由题意可知BC＝AB，DC＝AB，

∵在△ABD中，∠ABD＝∠ADB，

∴AB＝AD，

∴BC＝DC＝AD＝AB，

∴四边形ABCD为菱形，

∴AC⊥BD，

∴∠AOB＝90°；

（2）∵四边形ABCD为菱形，

∴OB＝OD．

在Rt△ABO中，∠AOB＝90°，AB＝5，cos∠ABD＝，

∴OB＝AB•cos∠ABD＝3，

∴BD＝2OB＝6．

22．解：（1）如图，连接AD、AC，过点A作AE⊥CD，垂足为E．测量步骤为：

①测量楼顶到地面的高度AB＝a（米）；

②在楼顶处测点D的俯角∠EAD＝α；

③在楼顶处测点C的仰角∠EAC＝β．

（2）在Rt△AED中，DE＝AB＝a，

∵∠ADE＝90°﹣α∴AE＝DEtan（90°﹣α）＝atan（90°﹣α），

在Rt△AEC中，CE＝AEtanβ＝atan（90°﹣α）tanβ，

∴CD＝DE+CE＝a+atanβtan（90°﹣α）＝a[1+tanβtan（90°﹣α）]．

23．解：在Rt△ODE中，DE＝15，∠ODE＝67°，

∵cos∠ODE＝，

∴OD≈≈38.46（cm），

∴OA＝OD﹣AD≈38.46﹣14≈24.5（cm）．

答：半径OA的长约为24.5cm．

24．解：（1）在Rt△CDE中，∠CDE＝30°，DE＝80cm，

∴CD＝80×cos45°＝80×＝40（cm），

答：支架CD的长为40cm；

（2）在Rt△OAC中，∠BAC＝30°，AC＝180cm，

∴OC＝AC×tan30°＝180×＝60（cm），

∴OD＝OC﹣CD＝60﹣40（cm），

∴AB＝AO﹣OB＝AO﹣OD＝60×2﹣（60﹣40）

＝60+40（cm），

答：真空热水管AB的长为（60+40）cm．