2022年九年级中考复习数学高分冲刺训练——几何综合：《四边形综合》(五)及答案

这是一份2022年九年级中考复习数学高分冲刺训练——几何综合：《四边形综合》(五)及答案，共27页。试卷主要包含了定义等内容，欢迎下载使用。

备战2022年九年级中考复习数学高分冲刺训练——几何综合：《四边形综合》（五）

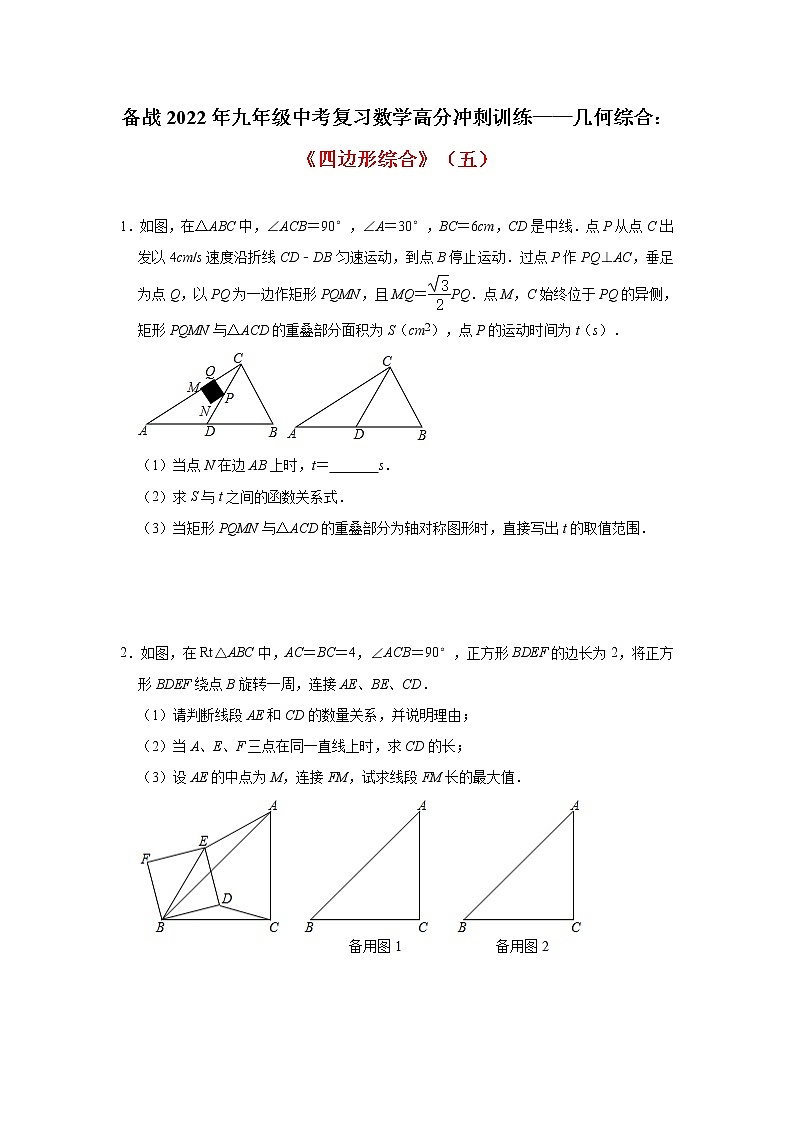
1．如图，在△ABC中，∠ACB＝90°，∠A＝30°，BC＝6cm，CD是中线．点P从点C出发以4cm/s速度沿折线CD﹣DB匀速运动，到点B停止运动．过点P作PQ⊥AC，垂足为点Q，以PQ为一边作矩形PQMN，且MQ＝PQ．点M，C始终位于PQ的异侧，矩形PQMN与△ACD的重叠部分面积为S（cm2），点P的运动时间为t（s）．

（1）当点N在边AB上时，t＝　 　s．
（2）求S与t之间的函数关系式．
（3）当矩形PQMN与△ACD的重叠部分为轴对称图形时，直接写出t的取值范围．



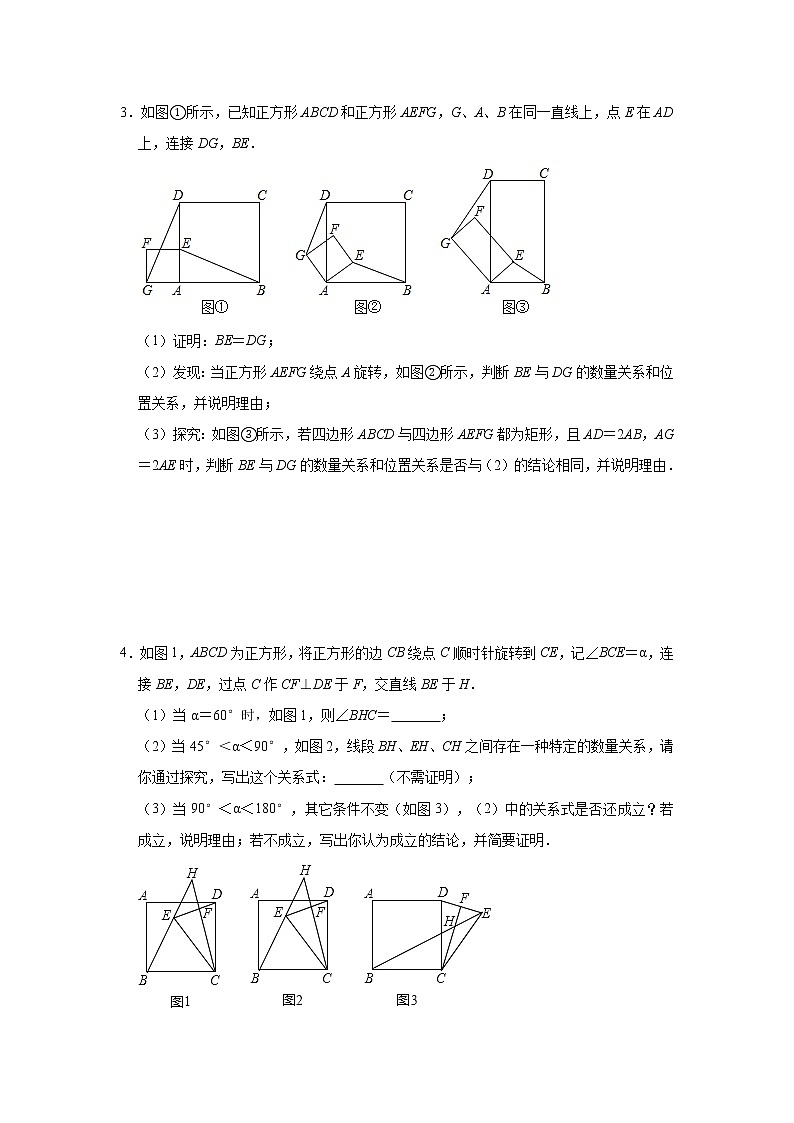
2．如图，在Rt△ABC中，AC＝BC＝4，∠ACB＝90°，正方形BDEF的边长为2，将正方形BDEF绕点B旋转一周，连接AE、BE、CD．
（1）请判断线段AE和CD的数量关系，并说明理由；
（2）当A、E、F三点在同一直线上时，求CD的长；
（3）设AE的中点为M，连接FM，试求线段FM长的最大值．



3．如图①所示，已知正方形ABCD和正方形AEFG，G、A、B在同一直线上，点E在AD上，连接DG，BE．

（1）证明：BE＝DG；
（2）发现：当正方形AEFG绕点A旋转，如图②所示，判断BE与DG的数量关系和位置关系，并说明理由；
（3）探究：如图③所示，若四边形ABCD与四边形AEFG都为矩形，且AD＝2AB，AG＝2AE时，判断BE与DG的数量关系和位置关系是否与（2）的结论相同，并说明理由．





4．如图1，ABCD为正方形，将正方形的边CB绕点C顺时针旋转到CE，记∠BCE＝α，连接BE，DE，过点C作CF⊥DE于F，交直线BE于H．
（1）当α＝60°时，如图1，则∠BHC＝　 　；
（2）当45°＜α＜90°，如图2，线段BH、EH、CH之间存在一种特定的数量关系，请你通过探究，写出这个关系式：　 　（不需证明）；
（3）当90°＜α＜180°，其它条件不变（如图3），（2）中的关系式是否还成立？若成立，说明理由；若不成立，写出你认为成立的结论，并简要证明．

5．四边形ABCD中，点E是AB的中点，F是AD边上的动点．连结DE、CF．
（1）若四边形ABCD是矩形，AD＝12，CD＝10，如图（1）．
①请直接写出AE的长度；
②当DE⊥CF时，试求出CF长度．
（2）如图（2），若四边形ABCD是平行四边形，DE与CF相交于点P．探究：当∠B与∠EPC满足什么关系时，成立？并证明你的结论．





6．我们把对称中心重合，四边分别平行的两个正方形之间的部分叫“方形环”，易知方形环四周的宽度相等．
一条直线l与方形环的边线有四个交点M、M′、N′、N．小明在探究线段MM′与N′N 的数量关系时，从点M′、N′向对边作垂线段M′E、N′F，利用三角形全等、相似及锐角三角函数等相关知识解决了问题．请你参考小明的思路解答下列问题：
（1）当直线l与方形环的对边相交时，如图1，直线l分别交AD、A′D′、B′C′、BC于M、M′、N′、N，小明发现MM′与N′N相等，请你帮他说明理由；
（2）当直线l与方形环的邻边相交时，如图2，l分别交AD、A′D′、D′C′、DC于M、M′、N′、N，l与DC的夹角为α，你认为MM′与N′N还相等吗？若相等，说明理由；若不相等，求出的值（用含α的三角函数表示）．




7．定义：我们把对角线互相垂直的四边形叫做神奇四边形．
顺次连接四边形各边中点得到的四边形叫做中点四边形．
（1）判断：
①在平行四边形、矩形、菱形中，一定是神奇四边形的是　 　；
②命题：如图1，在四边形ABCD中，AB＝AD，CB＝CD，则四边形ABCD是神奇四边形．此命题是　 　（填“真”或“假”）命题；
③神奇四边形的中点四边形是　 　；
（2）如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接BE，CG，GE．
①求证：四边形BCGE是神奇四边形；
②若AC＝2，AB＝，求GE的长；
（3）如图3，四边形ABCD是神奇四边形，若AB＝6，CD＝，AD、BC分别是方程x2﹣（k+4）x+4k＝0的两根，求k的值．



8．如图，平面直角坐标系中，菱形ABCD的边长为4，∠ABC＝60°，对角线AC与BD的交点E恰好在y轴上，点G是BC中点，直线AG交BD于F．
（1）点F的坐标为　 　；
（2）如图1，在x轴上有一动点H，连接FH，请求出FH+DH的最小值及相应的点H的坐标；
（3）如图2，若点N是直线AC上的一点，那么在直线AG上是否存在一点M，使得以B、F、M、N为顶点的四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由．






9．如图，正方形ABCD中，对角线AC，BD交于点O，点E，点F分别在线段OB，线段AB上，且AF＝OE，连接AE交OF于G，连接DG交AO于H．
（1）如图1，若点E为线段BO中点，AE＝，求BF的长；
（2）如图2，若AE平分∠BAC，求证：FG＝HG；
（3）如图3，点E在线段BO（含端点）上运动，连接HE，当线段HE长度取得最大值时，直接写出cos∠HDO的值．



10．已知矩形ABCD中，点E为AD上一点．

（1）连接BE、CE，∠BCE的平分线与AD交于点H，HG垂直平分BE．
①如图1，若AE＝8，BE＝10，求△EHC的面积；
②如图2，若∠ECD＝30°，求证：BC+CE＝HC；
（2）如图3，若AB＝CD＝6，AD＝BC＝8，连接CE，将△CDE沿CE翻折，使点D恰好落在对角线AC上的点F处，将△AFE绕点A顺时针旋转90°，再沿AB方向向下平移至△A′F′B处（点E与点B重合），将△A′F′B绕着点B顺时针旋转一个角α（0°＜α＜180°），在旋转过程中，设直线A′F′分别交直线AC、BC于点P、Q，是否存在这样的P、Q两点，使得△CPQ为等腰三角形？若存在，请直接写出CQ的长度；若不存在，请说明理由．

参考答案
1．解：（1）如图1中，

在Rt△ABC中，∵BC＝6cm，∠ACB＝90°，∠A＝30°，
∴AB＝2BC＝12cm，AC＝BC＝6cm，
∵AD＝DB，
∴CD＝AB＝6cm，
∵PN∥AC，
∴＝，
∴＝，
解得t＝，
故答案为．

（2）①如图2﹣1，当0＜t≤时，重叠部分是矩形PQMN，

∵CD＝AD，
∴∠A＝∠ACD＝30°
∴PQ＝PC＝×4t＝2t，
MQ＝PQ＝，
∴S＝S矩形PQMN＝t×2t＝2t2．

②如图2﹣2，当＜t≤时，重叠部分是五边形PQMEF，

∵CQ＝PCcos30°＝2t，AC＝BCtan60°＝6
∴AM＝AC﹣MQ﹣CQ＝6﹣t﹣2t＝6﹣3t，ME＝AM tan30°＝（6﹣3t）＝6﹣3t，EN＝MN﹣ME＝2t﹣（6﹣3t）＝5t﹣6，NF＝EN tan60°＝（5t﹣6），
∴S＝S矩形PQMN﹣S△ENF＝2t2﹣（5t﹣6）（5t﹣6）＝t2+30t﹣18．
③如图3，当＜t≤3时，重叠部分是五边形QMEDF．

∵AP＝AD+DP＝CD+DP＝4t，PQ＝APsin30°＝2t
∴NP＝MQ＝PQ＝t，EN＝NPtan30°＝t，DP＝AP﹣AD＝4t﹣6，
∴S＝S矩形PQMN﹣S△ENP﹣S△DFP＝2t2﹣tt﹣（4t﹣6）2＝t2+12t﹣9．

（3）观察图象可知当0＜t≤时，满足条件，
如图2﹣3中，当DE＝DF时，也满足条件，可得6﹣2t＝4t﹣6
解得t＝2，
综上所述，满足条件的t的值为0＜t≤或t＝2．
2．解：（1）结论：AE＝CD．
理由：∵在Rt△ABC中，AC＝BC＝4，∠ACB＝90°，
∴∠ABC＝∠EBD＝45°，
∴∠ABE＝∠CBD，
∵四边形BDEF是正方形，△ABC是等腰直角三角形，
∴＝，＝，
∴，
∴△ABE∽△CBD，
∴＝，
∴AE＝CD；

（2∵AC＝BC＝4，∠ACB＝90°，
∴AB＝BC＝4，
∵当A、E、F三点在一直线上时，
∵∠AFB＝90°，
∴AF＝＝＝2，
如图1，当AE在AB左上方时，


AE＝AF﹣EF＝2﹣2，
∵AE＝CD，
∴CD＝AE＝﹣，
如图2，当AE在AB右下方时，

同理，AE＝AF+EF＝2+2，
∴CD＝+，
综上所述，当A、E、F三点在一直线上时，CD的长为﹣或+；
（3）如图3，延长EF到G使FG＝EF，连接AG，BG，

则△BFG是等腰直角三角形，
∴BG＝BF＝2，
设M为AE的中点，
连接MF，
∴MF是△AGE的中位线，
∴AG＝2FM，
在△ABG中，∵AB﹣BG≤AG≤AB+BG，
∴2≤AG≤6，
∴≤FM≤3，
∴FM的最大值为3．
3．解：（1）证明：∵四边形ABCD和四边形AEFG是正方形，
∴AE＝AG，AB＝AD，∠BAD＝∠EAG＝90°，
∴△ABE≌△DAG（SAS），
∴BE＝DG；
（2）BE＝DG，BE⊥DG．
如图1中，∵四边形ABCD和四边形AEFG是正方形，
∴AE＝AG，AB＝AD，∠BAD＝∠EAG＝90°，
∴∠BAE＝∠DAG，
在△ABE和△DAG中，
，
∴△ABE≌△DAG（SAS），
∴BE＝DG；∠ABE＝∠ADG，
延长BE交AD于T，交DG于H．

∵∠ATB+∠ABE＝90°，
∴∠ATB+∠ADG＝90°，
∵∠ATB＝∠DTH，
∴∠DTH+∠ADG＝90°，
∴∠DHB＝90°，
∴BE⊥DG．
（3）数量关系不成立，DG＝2BE，位置关系成立．
如图2中，延长BE交AD于T，交DG于H．

∵四边形ABCD与四边形AEFG都为矩形，
∴∠BAD＝∠DAG，
∴∠BAE＝∠DAG，
∵AD＝2AB，AG＝2AE，
∴，
∴△ABE∽△ADG，
∴∠ABE＝∠ADG，，
∴DG＝2BE，
∵∠ATB+∠ABE＝90°，
∴∠ATB+∠ADG＝90°，
∵∠ATB＝∠DTH，
∴∠DTH+∠ADG＝90°，
∴∠DHB＝90°，
∴BE⊥DG．
4．解：（1）作CG⊥BH于G，如图1所示：
∵四边形ABCD是正方形，
∴CB＝CD，∠BCD＝90°，
由旋转的性质得：CE＝CB，∠BCE＝α＝60°，
∴CD＝CE，∠BCG＝∠ECG＝∠BCE＝30°，
∵CF⊥DE，
∴∠ECF＝∠DCF＝∠DCE，
∴∠GCH＝（∠BCE+∠DCE）＝×90°＝45°；
故答案为：45°；
（2）BH+EH＝CH；理由如下：
作CG⊥BE于G，如图2所示：
∵DC＝EC，
∴∠DCF＝∠ECF＝∠HCB+∠BCG+∠ECG，
∵BC＝EC，
∴∠BCG＝∠ECG，
∴∠DCF＝∠HCB+2∠BCG，
∴∠DCF+∠HCB＝2∠HCB+2∠BCG＝90°，
∴∠HCB+∠BCG＝45°，
∴∠H＝∠HCG＝45°，
∴△CGH是等腰直角三角形，
∴CH＝
⎷
2
GH，
∴BH+EH＝BH+BH+BG+EG＝2GH＝CH，
即：BH+EH＝CH．
（3）当90°＜α＜180°，其它条件不变，（2）中的关系式不成立，BH﹣EH＝CH；理由如下：
作CG⊥BH于G，如图3所示：
同（1）得：∠BHC＝45°，△CGH是等腰直角三角形，CH＝GH，BG＝EG＝BE，
∴BH﹣EH＝BG+GH﹣EH＝BG+EG﹣EH﹣EH＝2GH＝CH．



5．解：（1）①∵四边形ABCD是矩形，
∴AD＝BC，AB＝CD，∠A＝∠ADC＝90°．
∵AD＝12，CD＝10，
∴BC＝12，AB＝10．
∵点E是AB的中点，
∴AE＝AB＝5．
②∵DE⊥CF，
∴∠DPC＝∠DPF＝90°，
∴∠DFC+∠DCF＝90°，∠DFC+∠FDP＝90°，
∴∠DCF＝∠FDP．
∵∠A＝∠ADC，
∴△CFD∽△DEA，
∴．
在Rt△AED中，由勾股定理，得
ED＝13．
∴，
∴CF＝．
答：CF的长度为；
（2）当∠B+∠EPC＝180°时，
成立．
证明：∵四边形ABCD是平行四边形，
∴∠B＝∠ADC，AD∥BC，
∴∠B+∠A＝180°，
∵∠B+∠EPC＝180°，
∴∠A＝∠EPC＝∠FPD，
∵∠FDP＝∠EDA，
∴△DFP∽△DEA，
∴，
∵∠B＝∠ADC，∠B+∠EPC＝180°，∠EPC+∠DPC＝180°，
∴∠CPD＝∠CDF，
∵∠PCD＝∠DCF，
∴△CPD∽△CDF，
∴，
∴
∴，
即当∠B+∠EPC＝180°时，成立．

6．解　（1）在方形环中，∵M′E⊥AD，N′F⊥BC，AD∥BC，
在△MM′E与△NN′F中，
，
∴△MM′E≌△NN′F（AAS）．
∴MM′＝N′N；

（2）法一∵∠NFN′＝∠MEM′＝90°，∠FNN′＝∠EM′M＝α，
∴△NFN′∽△M′EM，
∴＝．
∵M′E＝N′F，
∴＝＝tanα（或）．
①当α＝45°时，tan α＝1，则MM′＝NN′；
②当α≠45°时，MM′≠NN′，则＝tanα（或）．
法二　在方形环中，∠D＝90°．
∵M′E⊥AD，N′F⊥CD，
∴M′E∥DC，N′F＝M′E．
∴∠MM′E＝∠N′NF＝α．
在Rt△NN′F与Rt△MM′E中，
sinα＝，cosα＝，即＝tanα（或）．
①当α＝45°时，MM′＝NN′；
②当α≠45°时，MM′≠NN′，则＝tanα（或）．
7．解：（1）①∵菱形的对角线互相垂直，
∴菱形是神奇四边形；
②∵AB＝AD，CB＝CD，
∴AC是BD的垂直平分线，
∴四边形ABCD是神奇四边形；
③如图，已知：四边形ABCD是神奇四边形，点E，点F，点G，点H分别是AD，DC，BC，AB的中点，

∵点E，点F，点G，点H分别是AD，DC，BC，AB的中点，
∴EF∥AC∥HG，BD∥EH∥FG，
∴四边形EFGH是平行四边形，
∵四边形ABCD是神奇四边形，
∴AC⊥BD，
又∵EF∥AC∥HG，BD∥EH∥FG，
∴EF⊥EH，
∴四边形EFGH是矩形，
故答案为矩形．
（2）①如图2，连接CE，BG交于点N，CE交AB于M，

∵四边形ACFG是正方形，四边形ABDE是正方形，
∴AB＝AE，AC＝AG，∠CAG＝∠BAE＝90°，
∴∠GAB＝∠CAE，
∴△GAB≌△CAE（SAS），
∴∠AEC＝∠ABG，
∵∠AEM+∠AME＝90°，
∴∠ABG+∠BMN＝90°，
∴∠BNM＝90°，
∴CE⊥BG，
∴四边形BCGE是神奇四边形；
②∵AC＝2，AB＝，
∴BC＝＝＝1，
∵四边形ACFG是正方形，四边形ABDE是正方形，AC＝2，AB＝，
∴CG＝AC＝2，BE＝AB＝，
∵GC2＝CN2+GN2，BE2＝BN2+NE2，BC2＝CN2+BN2，GE2＝GN2+NE2，
∴CG2+BE2＝BC2+GE2，
∴GE＝＝；
（3）∵四边形ABCD是神奇四边形，
∴同（2）中②的证明方法，可得AD2+BC2＝AB2+CD2，
∵AB＝6，CD＝，
∴AD2+BC2＝41，
∵AD、BC分别是方程x2﹣（k+4）x+4k＝0的两根，
∴AD+BC＝k+4，ADBC＝4k，
∵AD2+BC2＝41＝（AD+BC）2﹣2ADBC，
∴（k+4）2﹣8k＝41，
∴k1＝5，k2＝﹣5（不合题意舍去），
∴k＝5．
8．解：（1）如图1中，

∵四边形ABCD是菱形，∠ABC＝60°，
∴AB＝BC＝CD＝AD＝4，∠ABC＝∠ADC＝60°，CA⊥BD，
∴∠EDC＝∠EDA＝30°，∠CED＝90°，
∴EC＝CD＝2，∠ECD＝60°，
∵∠EOC＝90°，
∴∠CEO＝30°，
∴OC＝EC＝1，OE＝OC＝，
∴C（﹣1，0），E（0，），D（3，0），
∵AE＝EC，BE＝DE，
∴A（1，2），B（﹣3，2），
∴直线BC的解析式为y＝﹣x﹣，直线BD的解析式为y＝﹣x+，
∵AG⊥BC，
∴直线AG的解析式为y＝x+，
由，解得，
∴F（﹣1，）．
故答案为（﹣1，）．

（2）如图1﹣1中，过点D作射线DM，使得∠ODM＝30°，点点H作HK⊥OM于K，过点F作FJ⊥DM于J．

∵D（3，0），∠ODK＝30°，F（﹣1，），
∴直线DM的解析式为y＝x﹣，
∵FJ⊥DM，
∴直线FJ的解析式为y＝﹣x+，
由，解得，
∴J（，﹣），
∴FJ＝＝3，
在Rt△DHK中，∵∠KDH＝30°，
∴KH＝DH，
∴FH+DH＝FH+HK≥FJ，
∴FH+DH≥3，
∴FH+DH的最小值为3，此时点H的坐标为（，0）．

（3）如图2中，过点C作CM∥BF交AG于M，连接BM，CF．

∵△ABC是等边三角形，AG⊥BC，
∴BG＝CG，
∵∠BFG＝∠CMG，∠BGF＝∠CGM，
∴△BGF≌△CGM（AAS），
∴BF＝CM，
∵BF∥CM，
∴四边形BFCN＝M是平行四边形，
∴当点N与C重合时，四边形BFNM是平行四边形，此时N（﹣1，0），M（﹣3，）
根据对称性可知，当点N与N′关于点A对称时，四边形BFM′N′是平行四边形，此时N′（3，4），M′（5，），
如图3中，当BF是平行四边形的对角线时，BM″∥AC，

∵直线BM″的解析式为y＝x+5，直线AG的解析式为y＝x+，
由，解得，
∴M″（﹣5，0），
综上所述，满足条件的点M的坐标为（﹣3，）或（5，）或（﹣5，0）．
9．解：（1）∵四边形ABCD是正方形，
∴OA＝OB，AB＝OA，
∵点E为线段BO中点，
∴OE＝BE＝OB＝OA，
∵OE2+OA2＝AE2，且AE＝，
∴OE2+4OE2＝5，
∴OE＝1，
∴AF＝OE＝1，OB＝OA＝2，AB＝2，
∴BF＝AB﹣AF＝2﹣1；
（2）如图，延长HG交AB于M，

∵四边形ABCD是正方形，
∴∠OAB＝∠OBA＝∠OAD＝∠ODA＝45°，AC⊥BD，AO＝DO＝BO，
∵AE平分∠BAC，
∴∠BAE＝∠EAO＝22.5°，
∴∠DEA＝67.5°＝∠DAE，
∴AD＝DE＝AB，
∴AB﹣AF＝DE﹣OE，
∴BF＝DO＝BO，
∴∠BFO＝∠BOF＝67.5°，
∴∠AEO＝∠BOF＝67.5°，∠AOF＝∠EAO＝22.5°，
∴EG＝GO，AG＝GO，
∴AG＝GE，
又∵AD＝DE，
∴DM⊥AE，∠ADG＝∠EDG＝22.5°，
∴∠AMD＝67.5°＝∠BFO，
∴FG＝GM，
∵∠BAE＝∠EAO，AG＝AG，∠AGH＝∠AGM＝90°，
∴△AGM≌△AGH（ASA），
∴GM＝GH，
∴GF＝GH；
（3）如图，连接BH，

∵点E在OB上运动，∠BOH＝90°，
∴BH≥EH，
∴当点E与点B重合时，HE的长度有最大值，
如图，过点F作FN⊥BD，

∵AO＝BO＝DO，AC⊥BD，
∴AB＝OB，
∵OE＝AF，
∴BF＝OB﹣OB＝（﹣1）OB，
∵∠ABD＝45°，FN⊥BD，
∴FN＝BN＝＝OB，
∴DN＝BD﹣BN＝2OB﹣OB＝OB，
∴DF＝＝OB，
∴cos∠HDO＝＝．
10．（1）①解：如图1中，连接BH．

∵四边形ABCD是矩形，
∴∠A＝∠D＝90°，AB＝CD，
∵AE＝8，BE＝10，
∴AB＝CD＝＝＝6，
∵HG垂直平分线段BE，
∴BH＝EH，设BH＝EH＝x，
在Rt△ABH中，则有x2＝62+（8﹣x）2，
∴x＝5，
∴EH＝BH＝5，
∴S△CEH＝EHCD＝×5×6＝15．

②证明：如图2中，连接BH．

∵∠D＝∠DCB＝90°，∠ECD＝30°，
∴∠CED＝60°，∠ECB＝60°，
∵EC平分∠DCH，
∴∠ECD＝∠ECH＝30°，
∵∠CED＝∠EHC+∠ECH，
∴∠EHC＝∠ECH＝30°，
∴EH＝EC，
∵GH垂直平分线段BE，
∴BH＝EH＝CE，
∵EH∥BC，
∴四边形BCEH是等腰梯形，
∴∠ECB＝∠HBC＝60°，
∵BH＝CE，CB＝BC，
∴△ECB≌△HBC（SAS），
∴∠EBC＝∠HCB＝30°，
∴∠BEC＝90°，设DE＝a，则EC＝2DE＝2a，BC＝2EC＝4a，CD＝a．CH＝2a，
∴EC+BC＝6a＝2a＝CH．

（2）分4种情况：①当CP＝PQ时，如图3，此时P与A'重合，

∴∠PQB＝∠PCB，
∵∠BF'Q＝∠CBA＝90°，
∴△BQF'∽△ACB，
∴＝，
∵BF'＝EF＝3，
∴＝，
∴BQ＝5，
∴CQ＝5+8＝13．

②当CP＝CQ时，如图4，

∵∠F'A'B＝∠FAE＝∠ACB，
∴∠BA'Q＝∠PCQ，
∵∠A'QB＝∠PQC，
∴△PCQ∽△BA'Q，
∵PC＝CQ，
∴B'A'＝A'Q＝5，
Rt△BF'Q中，BF'＝3，F'Q＝4+5＝9，
∴BQ＝＝3，
∴CQ＝BQ﹣BC＝3﹣8．

③当CQ＝PQ时，如图5，

∴∠QCP＝∠CPQ，
∵∠BA'F'＝∠CAE＝∠PCQ，∠CQP＝∠A'QB，
∴∠CPQ＝∠A'BQ，
∴∠A'BQ＝∠BA'Q，
∴BQ＝A'Q，
设BQ＝x，则CQ＝8﹣x，A'Q＝x，F'Q＝4﹣x，
在Rt△BQF'中，由勾股定理得：32+（4﹣x）2＝x2，
x＝，
∴CQ＝8﹣＝．