初中数学湘教版九年级下册1.4 二次函数与一元二次方程的联系授课课件ppt

这是一份初中数学湘教版九年级下册1.4 二次函数与一元二次方程的联系授课课件ppt，共14页。PPT课件主要包含了s表示离天台的距离，t表示行驶的时间，0≤t≤2，以上关系反之也成立，无实数根，有两个交点，有两个相异的实数根，有一个交点，有两个相等的实数根，没有交点等内容，欢迎下载使用。

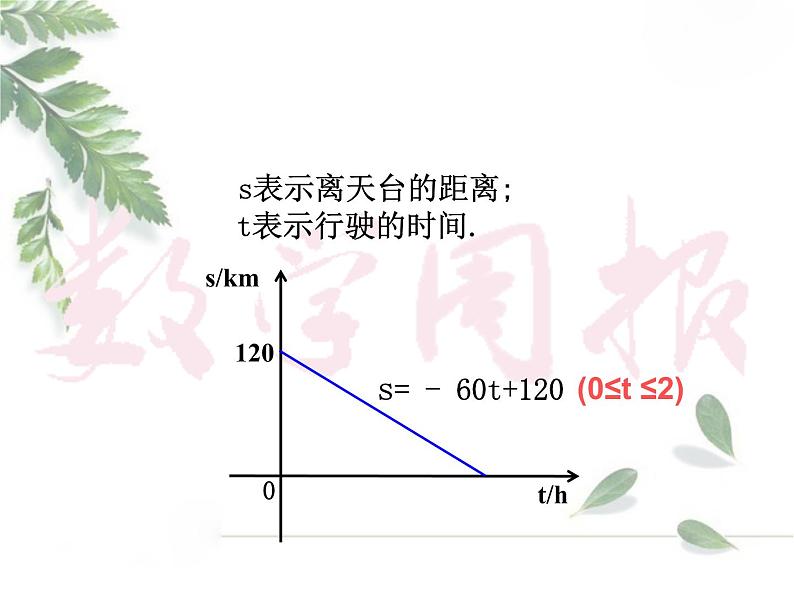
s= - 60t+120
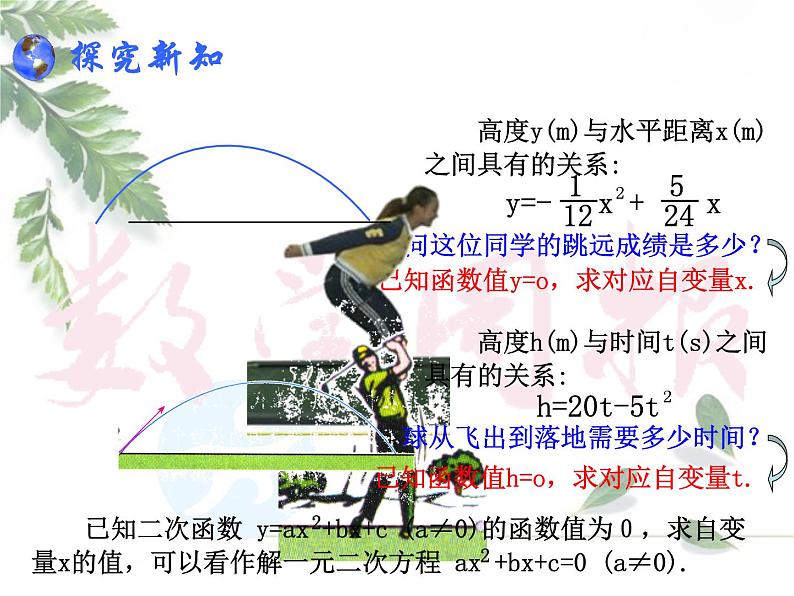
已知函数值y=，求对应自变量x.
请问这位同学的跳远成绩是多少？
高度y(m)与水平距离x(m)之间具有的关系:
高度h(m)与时间t(s)之间具有的关系:
球从飞出到落地需要多少时间？
已知函数值h=，求对应自变量t.
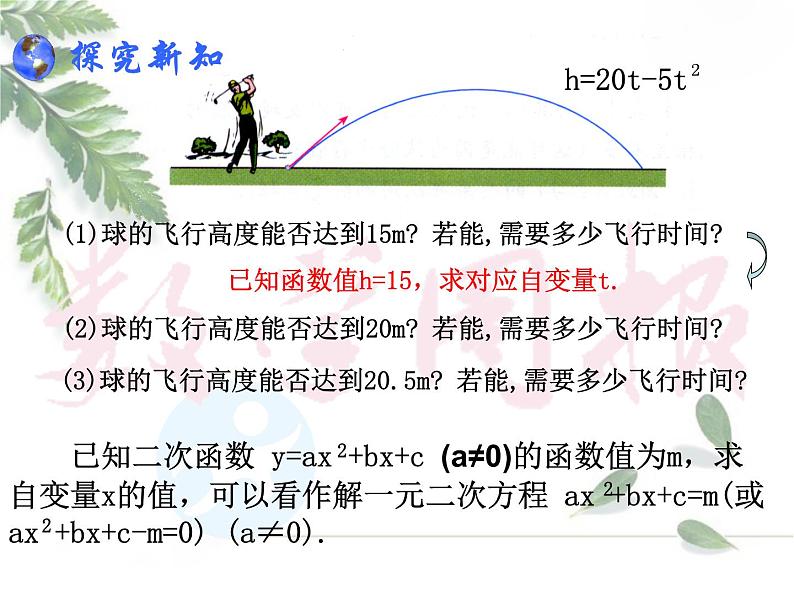
(1)球的飞行高度能否达到15m? 若能,需要多少飞行时间?
已知函数值h=15，求对应自变量t.
(2)球的飞行高度能否达到20m? 若能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m? 若能,需要多少飞行时间?
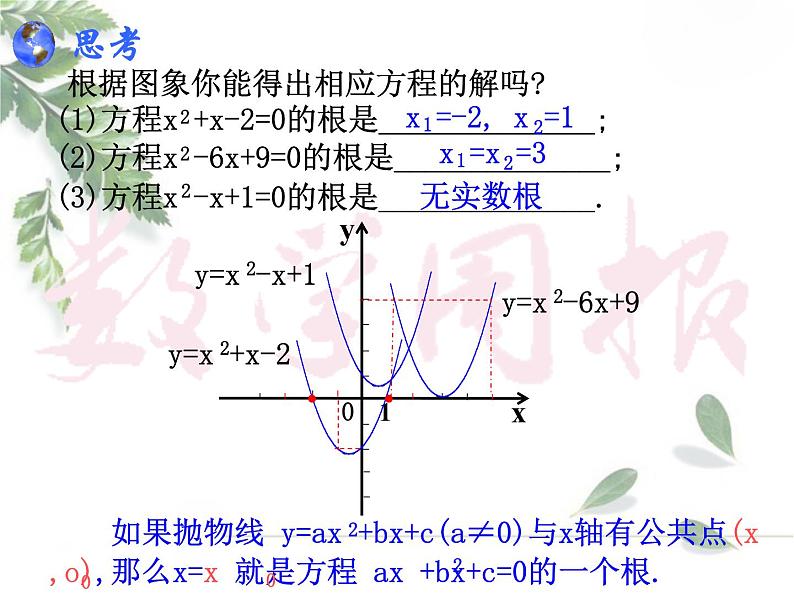
根据图象你能得出相应方程的解吗?
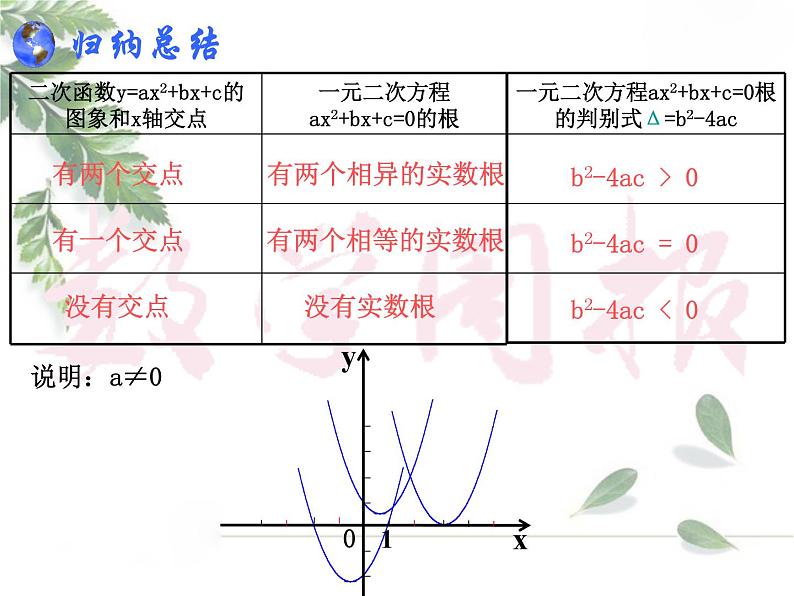
下列二次函数的图象与x轴有交点吗？有几个交点？
若此抛物线与 x轴有两个交点,求k的取值范围.
1.不与x轴相交的抛物线是( )A y=2x2 – 3 B y= - 2 x2 + 3 C y= - x2 – 3x D y=-2(x+1)2 - 3
2.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )A 无交点 B 只有一个交点 C 有两个交点 D不能确定
3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=＿＿＿＿,此时抛物线 y=x2-2x+m与x轴有＿＿个交点 .
4.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=＿＿＿＿.
5.若函数y=-x2+2kx+2与坐标轴交点的个数有 个.
6.已知抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx+c =0根的情况是( )A 有两个不相等的实数根B 有两个异号的实数根C有两个相等的实数根D 没有实数根
例: 利用函数图象求方程x2-2x-2=0的实数根 (精确到0.1)
解: 作y=x2-2x-2的图象(如图),它与x轴的公共点 的横坐标大约是 – 0.7 , 2.7 所以方程x2-2x-2=0的实数根为 x1≈-0.7, x2≈-2.7.
练习:根据下列表格的对应值: 判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )A 3

相关课件

数学九年级下册第1章 二次函数1.4 二次函数与一元二次方程的联系优秀ppt课件： 这是一份数学九年级下册<a href="/sx/tb_c104131_t3/?tag_id=26" target="_blank">第1章 二次函数1.4 二次函数与一元二次方程的联系优秀ppt课件</a>，文件包含湘教版数学九年级下册14《二次函数与一元二次方程的联系》课件pptx、湘教版数学九年级下册14《二次函数与一元二次方程的联系》教案doc等2份课件配套教学资源，其中PPT共29页， 欢迎下载使用。

湘教版九年级下册1.4 二次函数与一元二次方程的联系习题ppt课件： 这是一份湘教版九年级下册1.4 二次函数与一元二次方程的联系习题ppt课件，共23页。

数学湘教版第1章 二次函数1.4 二次函数与一元二次方程的联系习题ppt课件： 这是一份数学湘教版第1章 二次函数1.4 二次函数与一元二次方程的联系习题ppt课件，共17页。