数学九年级下册第1章 二次函数1.4 二次函数与一元二次方程的联系教案配套课件ppt

这是一份数学九年级下册第1章 二次函数1.4 二次函数与一元二次方程的联系教案配套课件ppt，共22页。PPT课件主要包含了探究新知，有两个不同的交点，有两个重合的交点，没有交点，随堂练习等内容，欢迎下载使用。

画出二次函数 y = x2– 2x – 3 的图象， 你能从图象中看出它与 x 轴的交点吗？二次函数 y = x2– 2x – 3 与一元二次方程 x2– 2x – 3 ＝ 0 有怎样的关系？
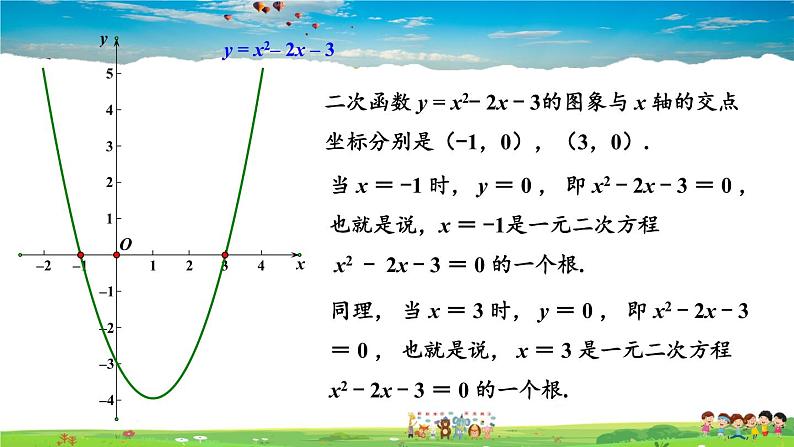
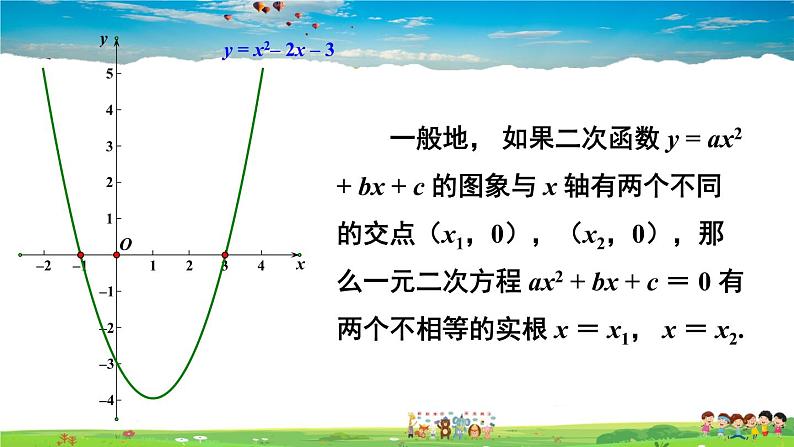
y = x2– 2x – 3
二次函数 y = x2- 2x - 3的图象与 x 轴的交点坐标分别是（-1，0），（3，0）.
当 x ＝ -1 时， y ＝ 0 ， 即 x2 - 2x - 3 ＝ 0 ， 也就是说，x ＝ -1是一元二次方程 x2 - 2x - 3 ＝ 0 的一个根.
同理， 当 x ＝ 3 时， y ＝ 0 ， 即 x2 - 2x - 3 ＝ 0 ， 也就是说， x ＝ 3 是一元二次方程 x2 - 2x - 3 ＝ 0 的一个根.
一般地， 如果二次函数 y = ax2 + bx + c 的图象与 x 轴有两个不同的交点（x1，0），（x2，0），那么一元二次方程 ax2 + bx + c ＝ 0 有两个不相等的实根 x ＝ x1， x ＝ x2.
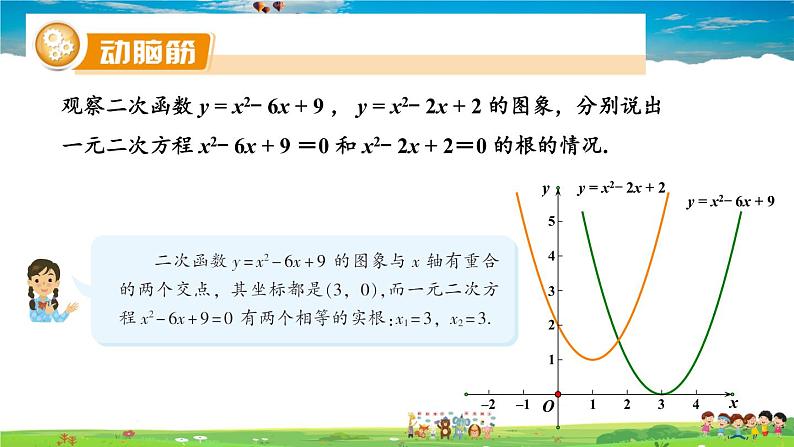
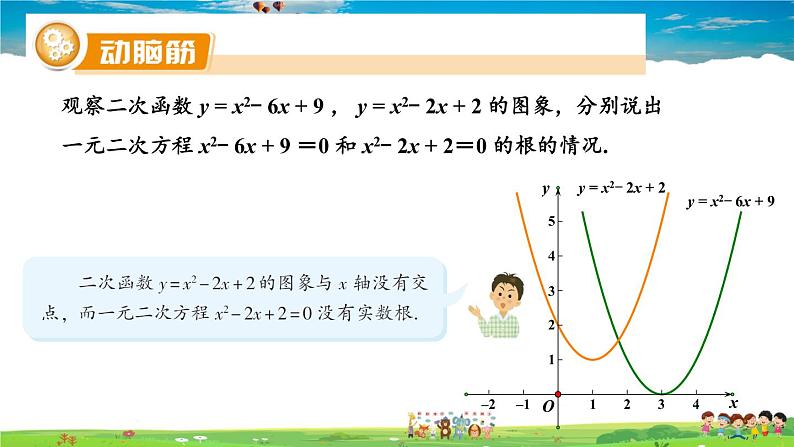
观察二次函数 y = x2- 6x + 9 ， y = x2- 2x + 2 的图象，分别说出一元二次方程 x2- 6x + 9 ＝0 和 x2- 2x + 2＝0 的根的情况.
y = x2- 6x + 9
y = x2- 2x + 2
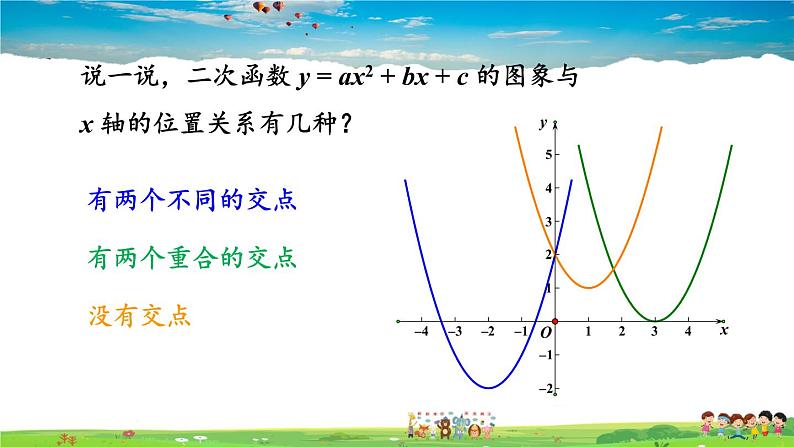
说一说，二次函数 y = ax2 + bx + c 的图象与 x 轴的位置关系有几种？
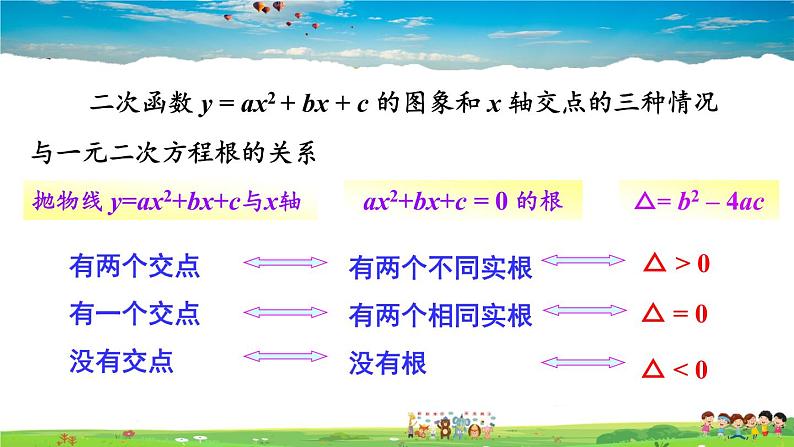
二次函数 y = ax2 + bx + c 的图象和 x 轴交点的三种情况与一元二次方程根的关系
ax2+bx+c = 0 的根
抛物线 y=ax2+bx+c与x轴
△= b2 – 4ac
有两个不同实根有两个相同实根没有根
有两个交点有一个交点没有交点
求一元二次方程 x2 － 2x － 1 ＝ 0 的根的近似值（精确到0.1）．
分析 一元二次方程 x2 － 2x － 1 ＝ 0 的根就是抛物线 y ＝ x2 － 2x－ 1 与 x 轴的交点的横坐标． 因此我们可以先画出这条抛物线， 然后从图象上找出它与 x 轴的交点的横坐标． 这种解一元二次方程的方法叫作图象法．
通过观察或测量， 可得抛物线与 x 轴的交点的横坐标约为－ 0.4 或 2.4， 即一元二次方程 x2 - 2x - 1 = 0 的实数根为 x1≈ - 0.4， x2 ≈ 2.4．
我们还可以借助计算器来分析所求方程的实数根. 将二次函数 y = x2 -2x - 1 在 -1 至 0 范围内的部分 x 值所对应的 y 值列表如下：
如图，丁丁在扔铅球时， 铅球沿抛物线 运行，其中 x 是铅球离初始位置的水平距离， y 是铅球离地面的高度.（1） 当铅球离地面的高度为 2.1 m 时， 它离初始位置的水平距离是多少？（2） 铅球离地面的高度能否达到 2.5 m， 它离初始位置的水平距离是多少？（3） 铅球离地面的高度能否达到 3 m？ 为什么？
（1） 当铅球离地面的高度为 2.1 m 时， 它离初始位置的水平距离是多少？
解（1） 由抛物线的表达式得
即 x2 - 6x + 5 = 0 ，解得 x1 = 1， x2 = 5.即当铅球离地面的高度为2.1 m时，它离初始位置的水平距离是1 m或5 m.
（2） 铅球离地面的高度能否达到 2.5 m， 它离初始位置的水平距离是多少？
（2） 由抛物线的表达式得
即 x2 - 6x + 9 = 0 ，解得 x1 = x2 = 3.即当铅球离地面的高度为 2.5 m 时，它离初始位置的水平距离是 3 m.
（3） 铅球离地面的高度能否达到 3 m？ 为什么？
（3） 由抛物线的表达式得
即 x2 - 6x + 14 = 0 ，因为 Δ = （-6）2 - 4×1×14 = -20 < 0,所以方程无实数根.所以铅球离地面的高度不能达到 3 m.
1.试判断下列抛物线与 x 轴的交点情况：（1） y ＝ x2 － x － 2 ； （2） y ＝ 9x2 ＋ 12x ＋ 4 ； （3） y ＝ x2 － 2x ＋ 3 ．
解：（1） x2 － x － 2 = 0，Δ =（-1）2-4×1×（-2）= 9 > 0与 x 轴有两个不同的交点.
（2） 9x2 +12 x + 4 = 0，Δ =（12）2-4×9×4= 0与 x 轴有两个相同的交点.
（3） x2 -2 x + 3 = 0，Δ =（-2）2-4×1×3= -8 < 0与 x 轴没有交点.
2. 用图象法求一元二次方程 x2＋ x － 1 ＝ 0 的根的 近似值（精确到 0.1）．
y = x2＋ x － 1
通过观察或测量， 可得抛物线与 x 轴的交点的横坐标约为－ 1.6 或 0.6， 即一元二次方程 x2 + x - 1 = 0 的实数根为 x1≈ - 1.6， x2 ≈ 0.6．
3.某**学校推出了一种高效环保型洗涤用品，年初上市后，**学校经历了从亏损到赢利的过程. 如图，已知 刻画了该**学校年初以来累积利润 y （万元）与销售时间 x（月份）之间的关系. 试根据图象提供的信息，回答下列问题：（1）该**学校亏损期是几个月？几月末开始赢利？（2）求截止到几月末**学校累积利润可达到 30 万元；（3）该**学校第 8 月末所获利润是多少？
（1）亏损期数是 4 个月，4月末开始盈利.（2）10月末累积利润可达到 30 万元.（3）第 8 月末利润是 16 万元.
二次函数 y＝x2＋3x－4 的图象与 x 轴交点的横坐标 是（ ） A．1 和 －4 B．－1 和 4 C．1 和 4 D．－1 和 －4
2. 下表是一组二次函数 y＝ax2＋bx＋c 的自变量 x与函数值 y 的对应值:那么方程 ax2＋bx＋c＝0 其中一个根的取值范围是（ ）A．1.0＜x＜1.1 B．1.1＜x＜1.2C．1.2＜x＜1.3 D．1.3＜x＜1.4
3. 根据表格中所给的对应值, 判断方程 ax2＋bx＋c＝2 (a ≠ 2, a, b, c 为常数)的根的个数是（ ） A．0 B．1 C．2 D．1或2