2020-2021学年广东省肇庆市端州区地质中学七年级（下）第二次段考数学试卷

2020-2021学年广东省肇庆市端州区地质中学七年级（下）第二次段考数学试卷

1. 在下列所给出坐标的点中在第二象限的是

A.  B.  C.  D.

2. 下列实数中，是无理数的是

A.  B.  C.  D.

3. 下列命题中是假命题的是

A. 对顶角相等
B. 同位角相等
C. 邻补角互补
D. 平行于同一条直线的两条直线平行

4. 下列方程中，是二元一次方程的是

A.  B.  C.  D.

5. 下列式子中，正确的是

A.  B.  C.  D.

6. 将点先向右平移3个单位，再向上平移5个单位得到点，则点的坐标为

A.  B.  C.  D.

7. 已知是二元一次方程的一组解，则m的值为

A.  B. 2 C.  D.

8. 如图，直线AB，CD相交于点O，射线OM平分，若，则等于
   
    

A.  B.  C.  D.

9. 某班学生分组搞活动，若每组7人，则余下4人；若每组8人，则有一组少3人．设全班有学生x 人，分成y 个小组，则可得方程组

A.  B.  C.  D.

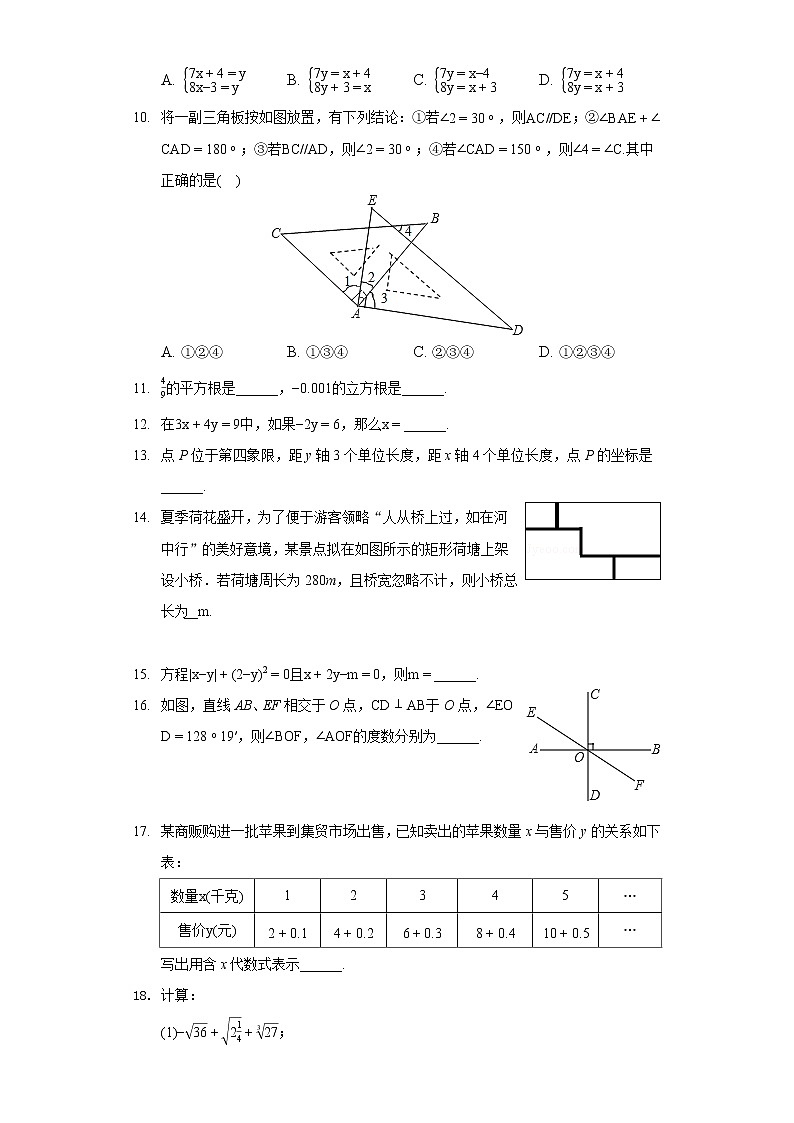
10. 将一副三角板按如图放置，有下列结论：①若，则；②；③若，则；④若，则其中正确的是

A. ①②④ B. ①③④ C. ②③④ D. ①②③④

11. 的平方根是______，的立方根是______.
12. 在中，如果，那么______.
13. 点P位于第四象限，距y轴3个单位长度，距x轴4个单位长度，点P的坐标是______.
14. 夏季荷花盛开，为了便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的矩形荷塘上架设小桥．若荷塘周长为280m，且桥宽忽略不计，则小桥总长为__
     
15. 方程且，则______.
16. 如图，直线AB、EF相交于O点，于O点，，则，的度数分别为______.
    
     

17. 某商贩购进一批苹果到集贸市场出售，已知卖出的苹果数量x与售价y的关系如下表：

写出用含x代数式表示______.

18. 计算：
    ；
    
    
    
    
    
    
    
     
19. 解方程：
    ；
    
    
    
    
    
    
    
     
20. 如图所示，，，，求的度数．
    
     

21. 已知，且y为正数，求的算术平方根和立方根．
    
    
    
    
    
    
     
22. 如图，已知：，垂足为点F，，垂足为点M，DM的延长线交AB于点B，点N在AD上，且
    若，求的度数；
    若，请你判断AB与MN的位置关系，并说明理由．
    
    
    
    
    
    
     
23. 在下列网格中建立平面直角坐标系如图，每个小正方形的边长均为1个单位长度．已知、和
    
    在图中标出点A、B、
    将点C向下平移3个单位到D点，将点A先向左平移3个单位，再向下平移1个单位到E点，在图中标出D点和E点．
    求的面积
    
    
    
    
    
    
     
24. 在“家电下乡”活动期间，凡购买指定家用电器的农村居民均可得到该商品售价的财政补贴．村民小李购买了一台A型洗衣机，小王购买了一台B型洗衣机，两人一共得到财政补贴351元，又知B型洗衣机售价比A型洗衣机售价多500元．求：
    型洗衣机和B型洗衣机的售价各是多少元？
    小李和小王购买洗衣机除财政补贴外实际各付款多少元？
    
    
    
    
    
    
     
25. 如图1，，的平分线交BC于点G，
    
    求证：；
    如图2，若，的平分线交AD于点E、交射线GA于点求的度数；
    如图3，线段AG上有一点P，满足，过点C作若在直线AG上取一点M，使，请直接写出的值．
    
    
    
    
    
    
    
    

答案和解析

1.【答案】B
 

【解析】解：第二象限内点的横坐标是负数，纵坐标是正数，
、、、中只有在第二象限．
故选：
根据第二象限内点的横坐标是负数，纵坐标是正数解答即可．
本题考查了点的坐标的知识，解答本题的关键在于记住各象限内点的坐标的符号．四个象限的符号特点分别是：第一象限；第二象限；第三象限；第四象限
 

2.【答案】D
 

【解析】解：A、是分数，属于有理数，故此选项不符合题意；
B、，是整数，属于有理数，故此选项不符合题意；
C、是有限小数，属于有理数，故此选项不符合题意；
D、是无理数，故此选项符合题意；
故选：
根据有理数和无理数的概念解答：无限不循环小数是无理数．
本题主要考查无理数的定义，特别注意在判定无理数前需先将能化简的数化简，属于简单题．
 

3.【答案】B
 

【解析】解：A、对顶角相等是真命题，故本选项正确，不符合题意；
B、两直线平行，同位角才相等，则同位角相等是假命题，故本选项错误，符合题意；
C、邻补角互补是真命题，故本选项正确，不符合题意；
D、平行于同一条直线的两条直线平行是真命题，故本选项正确，不符合题意；
故选
根据真命题与假命题的定义分别进行判断即可求出答案；正确的命题叫真命题，错误的命题叫做假命题．
此题考查了命题与定理，解题的关键是掌握真命题与假命题的定义，能根据有关性质对命题的真假进行判断．
 

4.【答案】B
 

【解析】解：中只含有一个未知数，所以不是二元一次方程；
B.含有两个未知数，并且含有未知数的项的次数都是1，是二元一次方程；
C.中未知数的次数是2次，所以不是二元一次方程；
D.方程中分母含有未知数，所以不是二元一次方程．
故选：
根据二元一次方程的概念求解可得．
本题主要考查二元一次方程的定义，解题的关键是掌握含有两个未知数，并且含有未知数的项的次数都是1，像这样的方程叫做二元一次方程．
 

5.【答案】A
 

【解析】解：A、，正确；
B、原式，错误；
C、原式，错误；
D、原式，错误，
故选：
原式各项计算得到结果，即可作出判断．
此题考查了立方根，以及算术平方根，熟练掌握各自的定义是解本题的关键．
 

6.【答案】A
 

【解析】解：将点先向右平移3个单位，再向上平移5个单位得到点，则点的坐标为，即，
故选：
让点A的横坐标加3，纵坐标加5即可得到平移后点的坐标．
本题考查点的平移规律；用到的知识点为：点的平移，左右平移只改变点的横坐标，左减右加；上下平移只改变点的纵坐标，上加下减．
 

7.【答案】B
 

【解析】解：把代入方程得：，
解得：
故选：
把x与y的值代入方程计算，即可求出m的值．
此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
 

8.【答案】A
 

【解析】解：与是对顶角，，
，
射线OM平分，

故选：
根据对顶角的定义得出，角平分线的定义得出，进而得出答案．
此题主要考查了对顶角、角平分线的定义，正确得出是解题的关键．
 

9.【答案】C
 

【解析】解：根据若每组7人，则余下4人，得方程；
根据若每组8人，则有一组少3人，得方程
可列方程组为
故选：
此题中的关键性的信息是：①若每组7人，则余下4人；②若每组8人，则有一组少3人．
考查了由实际问题抽象出二元一次方程组，根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．
 

10.【答案】A
 

【解析】解：，，


，

，
①的结论正确；
，，

②的结论正确；
，


③的结论错误；
，，



④的结论正确．
综上所述，正确的结论有：①②④，
故选：
利用平行线的判定与性质定理和角的和差的意义对每个选项进行逐一判断即可得出结论．
本题主要考查了平行线的判定与性质，充分利用平行线的判定与性质解答是解题的关键．
 

11.【答案】 
 

【解析】解：，，
故的平方根是，的立方根是，
故答案为：，
根据平方根和立方根的概念求解．
本题考查平方根和立方根，理解平方根和立方根的概念是解题关键．
 

12.【答案】7
 

【解析】解：，
，
把代入得，
，
解得，
故答案为：
先求出y的值，再把代入，解出方程即可．
本题考查了代数式的求值，掌握用数值代替代数式里的字母进行计算，正确计算结果是解题关键．
 

13.【答案】
 

【解析】解：点P位于第四象限，且距y轴3个单位长度，距x轴4个单位长度，
点P的横坐标为3，纵坐标为，即点P的坐标为
故答案为：
根据到x轴的距离即为纵坐标的绝对值、到y轴的距离即为横坐标的绝对值，再由第四象限点的坐标符号特点可得答案．
本题主要考查点的坐标，解题的关键是掌握到x轴的距离即为纵坐标的绝对值、到y轴的距离即为横坐标的绝对值及四个象限内点的坐标的符号特点．
 

14.【答案】140
 

【解析】

【分析】
此题主要考查了生活中的平移，根据已知正确平移小桥是解题关键．利用平移的性质直接得出答案即可．
【解答】
解：根据题意得出：小桥可以平移到矩形的边上，得出小桥的长等于矩形的长与宽的和，
故小桥总长为：
故答案为  

15.【答案】6
 

【解析】解：，而，，

解得，


故答案为：
利用非负数的性质求得x、y，进一步代入求得数值即可．
本题考查了非负数的性质．解题的关键是掌握非负数的性质：几个非负数的和为0时，这几个非负数都为
 

16.【答案】；
 

【解析】解：，
，



由垂直的定义，结合角的和差，先求出，再根据对顶角相等求的度数，再根据和是邻补角，求的度数．
本题考查对顶角的性质以及邻补角的定义，是一个需要熟记的内容．注意运用垂直的定义得角的度数是
 

17.【答案】
 

【解析】解：由表可知，，
故答案为：
由表知，售价是数量的倍，据此可得答案．
本题主要考查列代数式，解题的关键是根据表格得出售价是数量的倍及代数式的书写规范．
 

18.【答案】解：






 

【解析】首先计算开方和开立方，然后从左向右依次计算即可．
首先计算绝对值和乘法，然后从左向右依次计算即可．
此题主要考查了实数的运算，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．
 

19.【答案】解：，
由①，可得：③，
③代入②，可得：，
解得，
把代入③，解得，
原方程组的解是

，
①+②，可得，
解得，
把代入①，解得，
原方程组的解是
 

【解析】应用代入消元法，求出方程组的解是多少即可．
应用加减消元法，求出方程组的解是多少即可．
此题主要考查了解二元一次方程组的方法，注意代入消元法和加减消元法的应用．
 

20.【答案】解：，
，

 

【解析】根据两直线平行，内错角相等先求出，再与相加即可．
本题主要利用两直线平行，内错角相等的性质，需要熟练掌握．
 

21.【答案】解：，且y为正数，
，
，
，
 

【解析】先根据“，且y为正数”求出y的值，再求出的值，根据算术平方根和立方根的定义解答即可．
本题考查的是立方根、平方根以及算术平方根，熟知平方根及立方根的定义是解答此题的关键．
 

22.【答案】解：，，
，
，
，
，
，
，
，
，
；
理由如下：
，
，
，
，

解法二：，

，

 

【解析】首先证明可得，进而可得，可证明，根据平行线的性质即可求解；
由知，根据平行线的性质可得，结合已知条件可得，即可得
此题主要考查了平行线的判定和性质，关键是掌握两直线平行，同旁内角互补，内错角相等，两直线平行．两直线平行，内错角相等．
 

23.【答案】解：如图所示：A、B、C即为所求；

如上图所示：点D，E即为所求；

 

【解析】此题主要考查了平移变换以及三角形面积求法，正确掌握平移的规律是解题关键．
直接利用A，B，C点的坐标在坐标系中得出各点位置；
利用平移的性质得出各对应点位置；
利用所在长方形面积减去周围三角形面积进而得出答案．
 

24.【答案】解：设A型洗衣机的售价为x元，B型洗衣机的售价为y元．
根据题意可列方程组：，解得：
答：A型洗衣机的售价为1100元，B型洗衣机的售价为1600元．

小李实际付款为：元；
小王实际付款为：元
答：小李和小王购买洗衣机各实际付款957元和1392元．
 

【解析】可根据：“两人一共得到财政补贴351元；又知B型洗衣机售价比A型洗衣机售价多500元”来列出方程组求解．
根据得出的A，B洗衣机的售价根据补贴的规定来求出两人实际的付款额．
解题关键是找准描述语：“两人一共得到财政补贴351元；又知B型洗衣机售价比A型洗衣机售价多500元”，找出合适的等量关系，列出方程，再求解．
 

25.【答案】证明：，
，
平分，
，
；
解：①若点E在线段AD上，
平分，，
，
，
，
，
，
平分，
，
；
②若点E在DA的延长线上，如图4，
，，
；
解：有两种情况：
①当M在BP的下方时，如图5，
设，
，
，，
，
，
，
，
，
：：；
②当M在BP的上方时，如图6，
同理得：，
：：
综上，的值是或
 

【解析】根据平行线的性质与角平分线即可证明．
分两种情况：①若点E在线段AD上，先根据直角的平分线得：，由平行线的性质得：，，最后根据外角的性质可得的度数；
②若点E在DA的延长线上，根据外角的性质可直接得结论；
有两种情况：
①当M在BP的下方时，如图5，设，先根据已知计算，，根据平行线的性质得：，根据角的和与差计算的度数，可得结论；
②当M在BP的上方时，如图6，同理可得结论．
本题主要考查了角平分线的定义、三角形外角的性质、平行线的判定与性质及角的和与差，注意分类讨论思想的运用，本题容易丢解，要注意审题．