专题05 函数的概念及其表示、分段函数（重难点突破）-【教育机构专用】2022年秋季高一上精品讲义（新教材人教A版）

专题05 函数的概念及其表示、分段函数

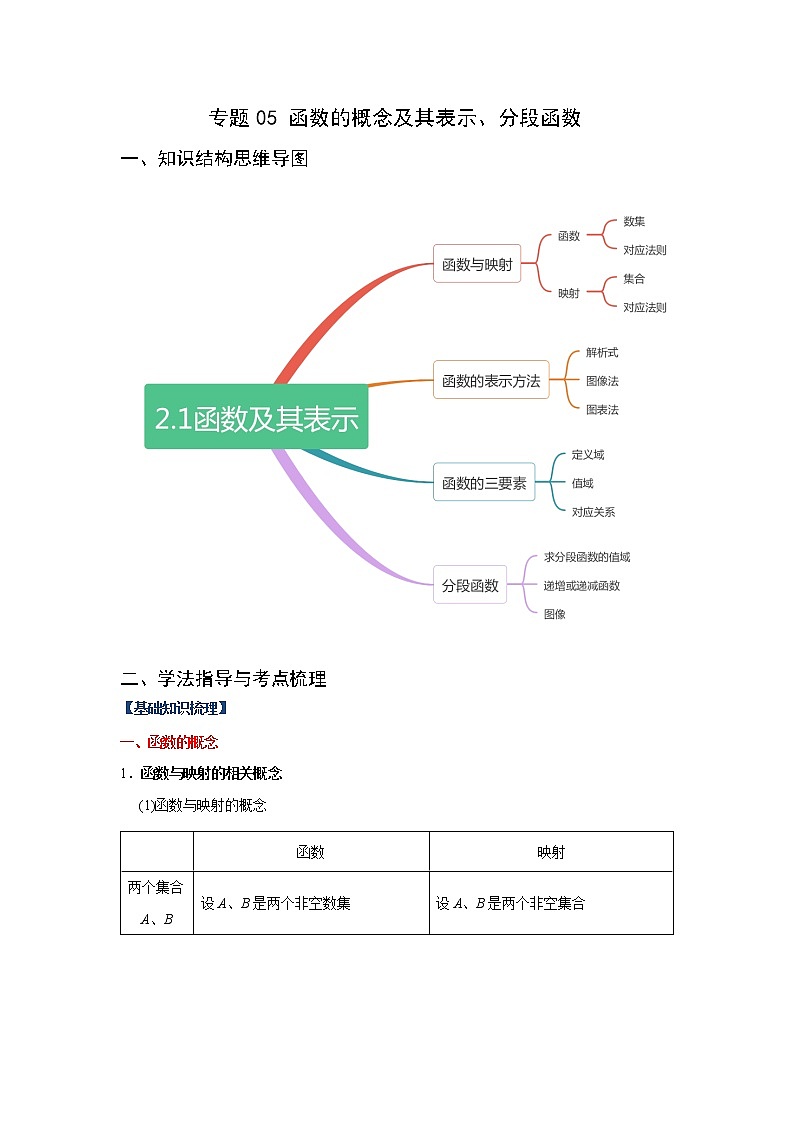
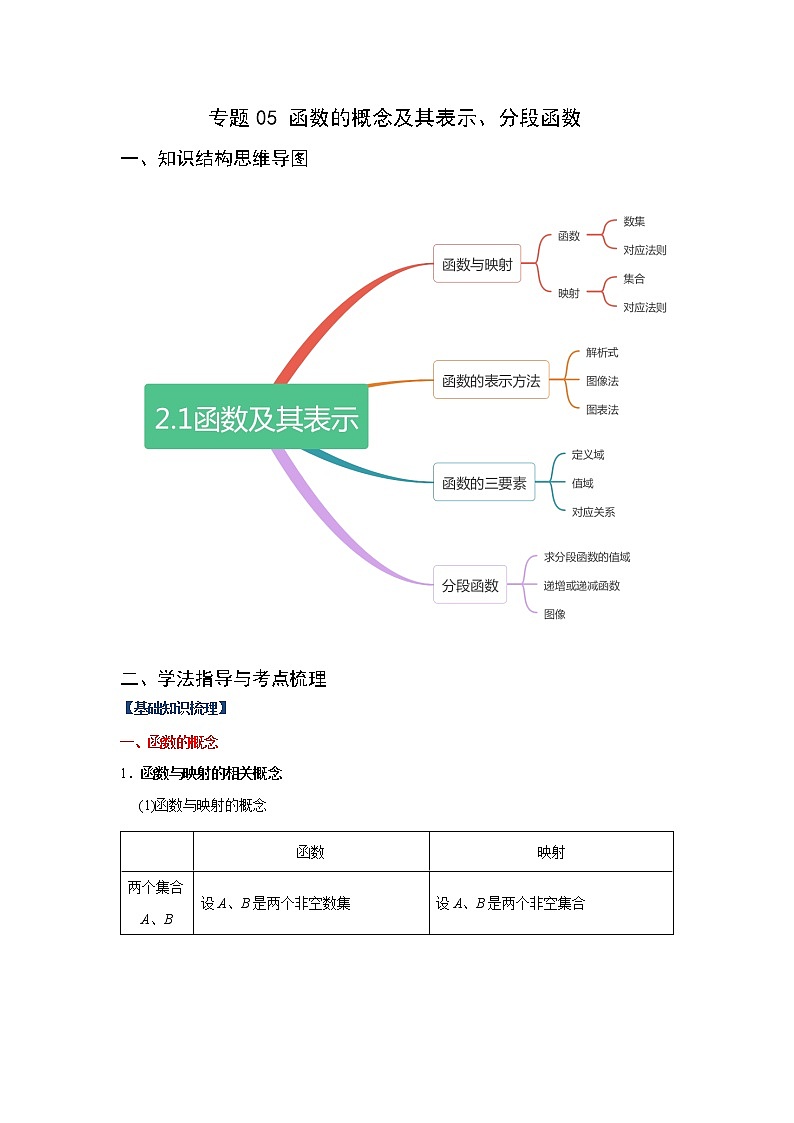
一、知识结构思维导图

二、学法指导与考点梳理

【基础知识梳理】

一、函数的概念

1．函数与映射的相关概念

(1)函数与映射的概念

注意：判断一个对应关系是否是函数关系，就看这个对应关系是否满足函数定义中“定义域内的任意一个自变量的值都有唯一确定的函数值”这个核心点．

(2)函数的定义域、值域

在函数y＝f(x)，x∈A中，x叫做自变量，x的取值范围A叫做函数的定义域，与x的值相对应的y值叫做函数值，函数值的集合{f(x)|x∈A}叫做函数的值域．

(3)构成函数的三要素

函数的三要素为定义域、值域、对应关系.

(4)函数的表示方法

函数的表示方法有三种：解析法、列表法、图象法.

解析法：一般情况下，必须注明函数的定义域；

列表法：选取的自变量要有代表性，应能反映定义域的特征；

图象法：注意定义域对图象的影响.

二、函数的三要素

1．函数的定义域

函数的定义域是使函数解析式有意义的自变量的取值范围，常见基本初等函数定义域的要求为：

(1)分式函数中分母不等于零.

(2)偶次根式函数的被开方式大于或等于0.

(3)一次函数、二次函数的定义域均为R.

(4)y＝x0的定义域是{x|x≠0}.

2．函数的解析式

(1)函数的解析式是表示函数的一种方式，对于不是y＝f(x)的形式，可根据题目的条件转化为该形式.

(2)求函数的解析式时，一定要注意函数定义域的变化，特别是利用换元法(或配凑法)求出的解析式，不注明定义域往往导致错误.

3．函数的值域

函数的值域就是函数值构成的集合，熟练掌握以下四种常见初等函数的值域：

(1)一次函数y＝kx＋b(k为常数且k≠0)的值域为R.

(2)反比例函数(k为常数且k≠0)的值域为(−∞，0)∪(0，＋∞)．

(3)二次函数y＝ax2＋bx＋c(a，b，c为常数且a≠0)，

当a>0时，二次函数的值域为；

当a<0时，二次函数的值域为.

求二次函数的值域时，应掌握配方法：.

三、分段函数

分段函数的概念

若函数在其定义域的不同子集上，因对应关系不同而分别用几个不同的式子来表示，则这种函数称为分段函数．分段函数虽由几个部分组成，但它表示的是一个函数．

【知识拓展】

1．(1)相等函数—如果两个函数的定义域相同，并且对应关系完全一致，则这两个函数相等．

①两个函数是否是相等函数，取决于它们的定义域和对应关系是否相同，只有当两个函数的定义域和对应关系完全相同时，才表示相等函数．

②函数的自变量习惯上用x表示，但也可用其他字母表示，如：f(x)＝2x−1，g(t)＝2t−1，h(m)＝2m−1均表示相等函数.

(2)映射的个数

若集合A中有m个元素，集合B中有n个元素，则从集合A到集合B的映射共有个．

2．分段函数的定义域等于各段函数的定义域的并集，其值域等于各段函数的值域的并集．

三、重难点题型突破

(一)、判断对应关系（图像）是否为函数.

1．判断对应关系是否为函数的2个条件

(1)A，B必须是非空实数集．

(2)A中任意一元素在B中有且只有一个元素与之对应．

对应关系是“一对一”或“多对一”的是函数关系，“一对多”的不是函数关系．

例1．（2020·全国高一课时练习）下列对应或关系式中是A到B的函数的序号为________.

①，；

②A＝{1，2，3，4}，B＝{0，1}，对应关系如图：

③，；

④，.

【变式训练1】（2019·广东禅城 佛山一中高一月考）（多选题）下列四个图形中可能是函数y＝f（x）图象的是（　　）

A． B． 

C． D．

【变式训练2】下列四个图象中，是函数图象的是　　

①             ②                ③               ④

A．① B．①③④ C．①②③ D．③④

【变式训练3】．（2012·全国高一课时练习）设集合，，那么下面的4个图形中，能表示集合M到集合N的函数关系的有（　　）

A． B． C． D．

(二)、求函数的定义域.

1．求函数定义域的三种常考类型及求解策略

(1)已知函数的解析式：构建使解析式有意义的不等式(组)求解．

(2)抽象函数：

①若已知函数f(x)的定义域为[a，b]，则复合函数f(g(x))的定义域由a≤g(x)≤b求出．

②若已知函数f(g(x))的定义域为[a，b]，则f(x)的定义域为g(x)在x∈[a，b]时的值域．

(3)实际问题：既要使构建的函数解析式有意义，又要考虑实际问题的要求．

2．求函数定义域的注意点

(1)不要对解析式进行化简变形，以免定义域变化．

(2)当一个函数由有限个基本初等函数的和、差、积、商的形式构成时，定义域一般是各个基本初等函数定义域的交集．

(3)定义域是一个集合，要用集合或区间表示，若用区间表示，不能用“或”连接，而应该用并集符号“∪”连接.

例2．（1）（2019·浙江南湖 嘉兴一中高一月考）下列函数中，与函数有相同定义域的是（    ）

A． B． C． D．

（2）（2019秋•金山区校级期末）下列各组函数中表示同一函数的是（　　）

A．y＝20与y B．y＝±1与y 

C．y与y D．y＝x+1与y

【变式训练1】求下列函数的定义域．

（1）；                    （2）；

（3）；                    （4）；

（5）．

例3．（2019·哈尔滨市第一中学校高三开学考试（文））已知的定义域为，则函数的定义域为 （    ）

A． B． C． D．

【变式训练1】（1）已知的定义域为，，求函数的定义域；

（2）已知的定义域为，，求函数的定义域．

（3）已知函数的定义域为，，求函数的定义域．

（4）已知函数的定义域为，，求函数的定义域．

(三)、判断函数为同一（相等）函数

判断函数相等的方法

(1)先看定义域，若定义域不同，则不相等；

(2)若定义域相同，再化简函数的解析式，看对应关系是否相同．

例4．（2020·江苏省响水中学高一月考）下列选项中，表示的是同一函数的是（    ）

A． B．

C． D．

【变式训练1】.（2019·江苏姑苏 苏州中学高一期中）（多选题）下列各组函数中，两个函数是同一函数的有（    ）

A．与 B．与

C．与 D．与

(四)、求函数的解析式

求函数解析式常用的方法

1．换元法：

已知复合函数f(g(x))的解析式，可用换元法，此时要注意新元的取值范围；

2．配凑法：

由已知条件f(g(x))＝F(x)，可将F(x)改写成关于g(x)的表达式，然后以x替代g(x)，便得f(x)的表达式；

3．待定系数法：

若已知函数的类型(如一次函数、二次函数)可用待定系数法；

4．方程组法：

已知关于f(x)与或f(－x)的表达式，可根据已知条件再构造出另外一个等式组成方程组，通过解方程求出f(x).

例5．（2020·全国高一）设函数，满足，则（    ）

A． B． C． D．

【变式训练1】.（2020·河北衡水中学调研）已知f(x)是二次函数，且f(0)＝0，f(x＋1)＝f(x)＋x＋1，求f(x)的解析式．

例6．（2017·全国高一课时练习）已知，则的解析式为（ 　 ）

A． B．

C． D．

【变式训练1】．已知函数是一次函数，且恒成立，则(    )

A．1 B．3

C．5 D．7

例7．（2020·全国高一）若函数满足，则___________．

【变式训练1】．（2020·全国高一）对的所有实数，函数满足，求的解析式．

【变式训练2】.（2019秋•武汉期末）（1）已知，求；

（2）已知，求f（x）的解析式．

(五)、求函数值域

求函数值域的基本方法

1．观察法：

通过对函数解析式的简单变形，利用熟知的基本函数的值域，或利用函数图象的“最高点”和“最低点”，观察求得函数的值域．

2．利用常见函数的值域：

一次函数的值域为；反比例函数的值域为；指数函数的值域为；对数函数的值域为；正、余弦函数的值域为；正切函数的值域为.

3．分离常数法：

将形如(a≠0)的函数分离常数，变形过程为：

，再结合x的取值范围确定的取值范围，从而确定函数的值域.

4．换元法：

对某些无理函数或其他函数，通过适当的换元，把它们化为我们熟悉的函数，再用有关方法求值域．如：函数，可以令，得到，函数可以化为(t≥0)，接下来求解关于t的二次函数的值域问题，求解过程中要注意t的取值范围的限制．

5．配方法：

对二次函数型的解析式可以先进行配方，在充分注意到自变量取值范围的情况下，利用求二次函数的值域的方法求函数的值域．

6．数形结合法：

作出函数图象，找出自变量对应的范围或分析条件的几何意义，在图上找出值域．

7．单调性法：

函数单调性的变化是求最值和值域的依据，根据函数的单调区间判断其单调性，进而求函数的最值和值域．

8．判别式法：

将函数转化为二次方程：若函数y＝f(x)可以化成一个系数含有y的关于x的二次方程a(y)x2＋b(y)x＋c(y)＝0，则在a(y)≠0时，由于x，y为实数，故必须有Δ＝b2(y)－4a(y)·c(y)≥0，由此确定函数的值域．

利用判别式求函数值的范围，常用于一些“分式”函数、“无理”函数等，使用此法要特别注意自变量的取值范围.

例8．（2019·东台创新高级中学高三月考）函数的值域是 _____.

例9．求下列函数的值域：

（1）；  （2）；  （3）.

【变式训练1】．求下列函数的值域

（1），，；            （2）．

（3），，；                （4）．

（5）         （6）        （7）．

【变式训练2】．（2020·全国高一课时练习）（多选题）已知函数，关于函数的结论正确的是（    ）

A．的定义域为 B．的值域为

C． D．若，则x的值是

E.的解集为

(六)、分段函数求值

分段函数是一类重要的函数，常作为考查函数知识的最佳载体，以其考查函数知识容量大而成为高考的命题热点，多以选择题或填空题的形式呈现，重点考查求值、解方程、零点、解不等式、函数图象及性质等问题，难度一般不大，多为容易题或中档题. 分段函数问题的常见类型及解题策略：

1．求函数值：

弄清自变量所在区间，然后代入对应的解析式，求“层层套”的函数值，要从最内层逐层往外计算．

2．求函数最值：

分别求出每个区间上的最值，然后比较大小．

3．求参数：

“分段处理”，采用代入法列出各区间上的方程或不等式．

4．解不等式：

根据分段函数中自变量取值范围的界定，代入相应的解析式求解，但要注意取值范围的大前提．

例10．（2019·浙江南湖 嘉兴一中高一月考）已知，若，则______________.

例11．（2020·全国高一课时练习）已知则不等式的解集是________.

【变式训练1】．（1）已知函数，若，则x=___________

（2）．（2020·四川省成都市郫都区第四中学高一期末）设函数，若f（x0）＞1，则x0的取值范围是（　　）

A．（﹣∞，﹣1）∪（1，+∞） B．（﹣∞，﹣1）∪[1，+∞）

C．（﹣∞，﹣3）∪（1，+∞） D．（﹣∞，﹣3）∪[1，+∞）

四、课堂定时训练（45分钟）

1.下列四个图象中，不是函数图象的是(　　)

A　         　B　　        C　         　D

2．（2020·重庆巴蜀中学高二期中）若函数满足，则的解析式是（    ）

A． B．

C． D．

3.（2020·全国高一课时练习）求下列函数的定义域.

（1）y＝3－；

（2）y＝－；

（3）y＝；

（4）y＝－＋.

4．（2020·全国高一课时练习）根据下列条件，求f(x)的解析式.

（1）f(x)是一次函数，且满足3f(x＋1)－f(x)＝2x＋9；

（2）f(x＋1)＝x2＋4x＋1；

（3）.

5．（2020·全国高一）已知的定义域为，

（1）求的定义域；

（2）求的定义域

6.已知，求．

7.设二次函数满足，且，求的解析式．

8．（2020·浙江省高三其他）已知函数，则________；的图象与坐标轴围成的图形的面积是________.

9．（2019·大连市普兰店区第一中学高一期末）已知函数，则______，若，则______.

10．（2018·全国高一课时练习）已知f(x)=

(1)若f(a)=4,且a>0,求实数a的值;

(2)求f的值.

11．（2020·全国高一）已知函数.

（1）求，的值；

（2）求证：是定值；

（3）求的值．

12．（2020·全国高一）若函数的定义域为R，则m的取值范围为多少？