第八章立体几何专题训练（十三）—计算体积（大题）-【新教材】2021-2022学年人教A版（2019）高中数学必修第二册专项训练

这是一份第八章立体几何专题训练（十三）—计算体积（大题）-【新教材】2021-2022学年人教A版（2019）高中数学必修第二册专项训练，共8页。
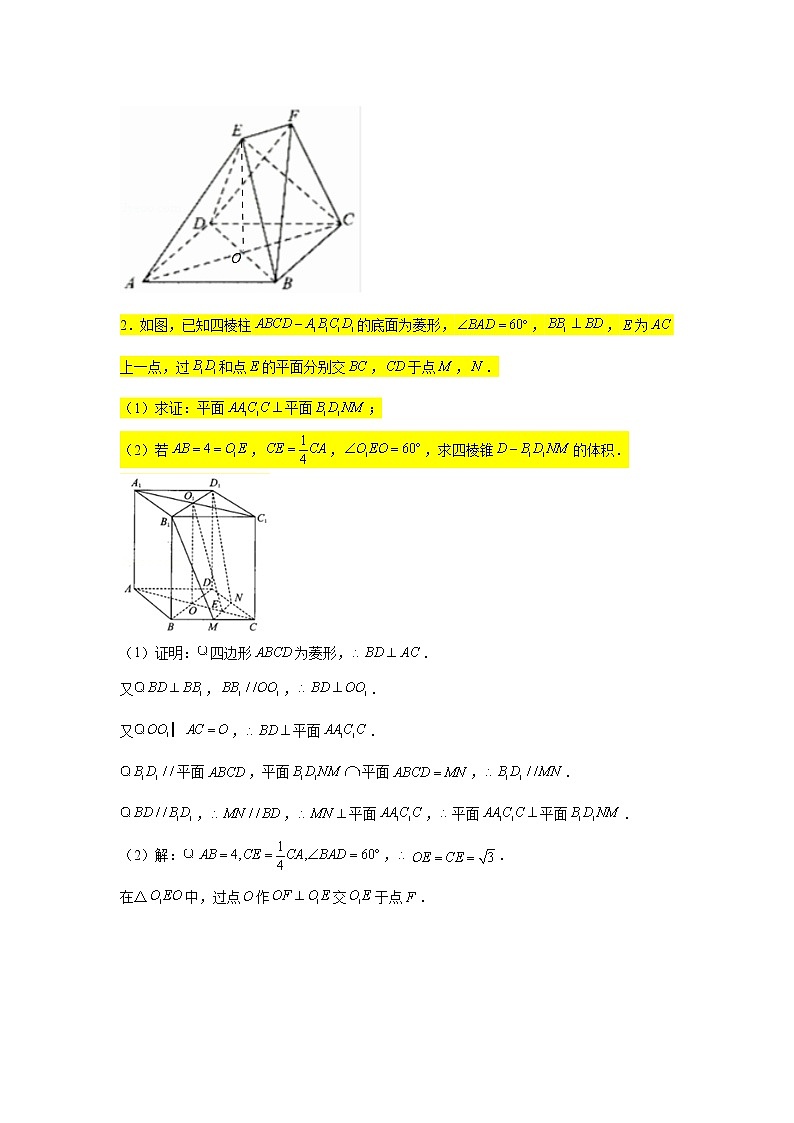
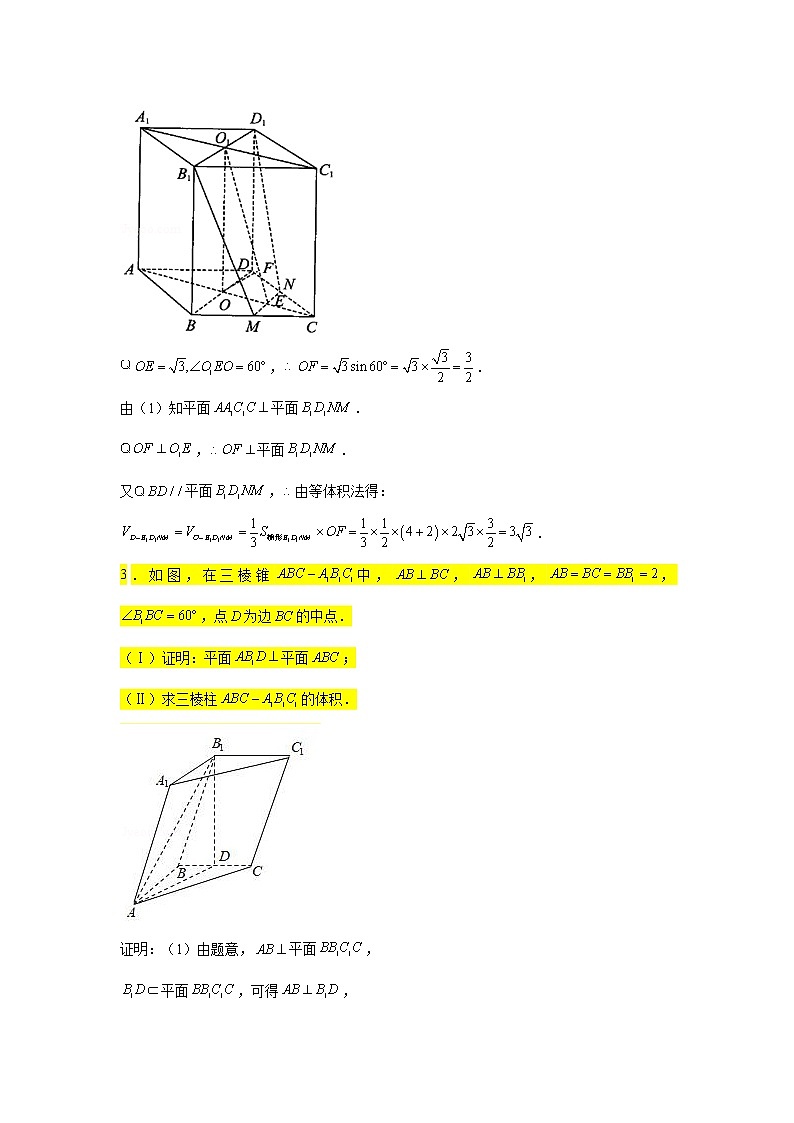
第八章  立体几何专练（十三）—计算体积（大题）1．如图，在多面体中，四边形是边长为2的菱形，，，．（Ⅰ）求证：平面平面；（Ⅱ）若，，，求多面体的体积．解：（Ⅰ）证明：设与交于，连接，由于，可得，由四边形为菱形，可得，由于，可得平面四边形，而，为平面内的两条相交直线，所以平面，而平面，所以平面平面；（Ⅱ）由，，可得，，由，，可得，由，可得，可得为梯形的高，又，所以梯形的面积为，由平面，可得多面体的体积为．2．如图，已知四棱柱的底面为菱形，，，为上一点，过和点的平面分别交，于点，．（1）求证：平面平面；（2）若，，，求四棱锥的体积．（1）证明：四边形为菱形，．又，，．又，平面．平面，平面平面，．，，平面，平面平面．（2）解：，．在△中，过点作交于点．，．由（1）知平面平面．，平面．又平面，由等体积法得：．3．如图，在三棱锥中，，，，，点为边的中点．（Ⅰ）证明：平面平面；（Ⅱ）求三棱柱的体积．证明：（1）由题意，平面，平面，可得，又△为等边三角形，点为边的中点，可得，与相交于点，则平面，平面，平面平面．解：（2）因为为直角三角形，，所以，由（1）可知，在直角三角形中，，，可得，故，所以，三棱柱的体积的体积为．4．如图，在长方形中，，，、为线段的三等分点，、为线段的三等分点．将长方形卷成以为母线的圆柱的半个侧面，、分别为圆柱上、下底面的直径．（1）证明：平面平面；（2）若为的中点，求三棱锥的体积．证明：（1）因为在下底面圆周上，且为下底面半圆的直径所以，又因为，且，所以平面，因为平面，所以平面平面，解：（2）设下底面半径为，由题，所以，因为下底面半圆圆心为，所以又因为、为的三等分点，所以，，均为边长等于1的等边三角形，所以的面积，所以三棱锥的体积．5．如图，已知四棱锥的底面是边长为的菱形，，点是棱的中点，，点在平面的射影为，为棱上一点．（Ⅰ）求证：平面平面；（Ⅱ）若平面，，求四棱锥的体积．证明：（1）平面，平面，依题意是等边三角形，为棱的中点，，又，，平面，平面，平面，平面平面．解：（Ⅱ）取的中点，连结，，底面是菱形，是棱的中点，，平面，平面，平面，平面，，平面平面，又平面平面，平面平面，，为的中点，，点到平面的距离为，四棱锥的体积：．6．如图，在四棱锥中，平面，底面是菱形，，，其中，为与的交点，为棱上一点．（1）求证：平面平面；（2）若平面，求三棱锥的体积的最大值．证明：（1）平面，平面，，四边形是菱形，，又，平面，平面，平面平面．解：（2）连结，取的中点，连结，平面，平面平面，平面，，是的中点，是的中点，四边形是菱形，，，又，，平面，且，．由基本不等式．当且仅当时取等号，即三棱锥的体积的最大值为．7．在四棱锥中，底面是矩形，平面，是等腰三角形，，是上一点，且三棱锥与四棱锥的体积之比为，与的延长线交于点，连接．（Ⅰ）求证：平面平面；（Ⅱ）若三棱锥的体积为，求线段的长．解：（Ⅰ）证明：平面，，底面是矩形，，平面，平面平面；（Ⅱ）三棱锥与四棱锥的体积之比为，，，设，，则，得，又，，得，，得，即．