第八章立体几何专题训练（十）—证明平行、垂直（1）-【新教材】2021-2022学年人教A版（2019）高中数学必修第二册专项训练

这是一份第八章立体几何专题训练（十）—证明平行、垂直（1）-【新教材】2021-2022学年人教A版（2019）高中数学必修第二册专项训练，共7页。试卷主要包含了如图，如图，四面体中，，，平面等内容，欢迎下载使用。
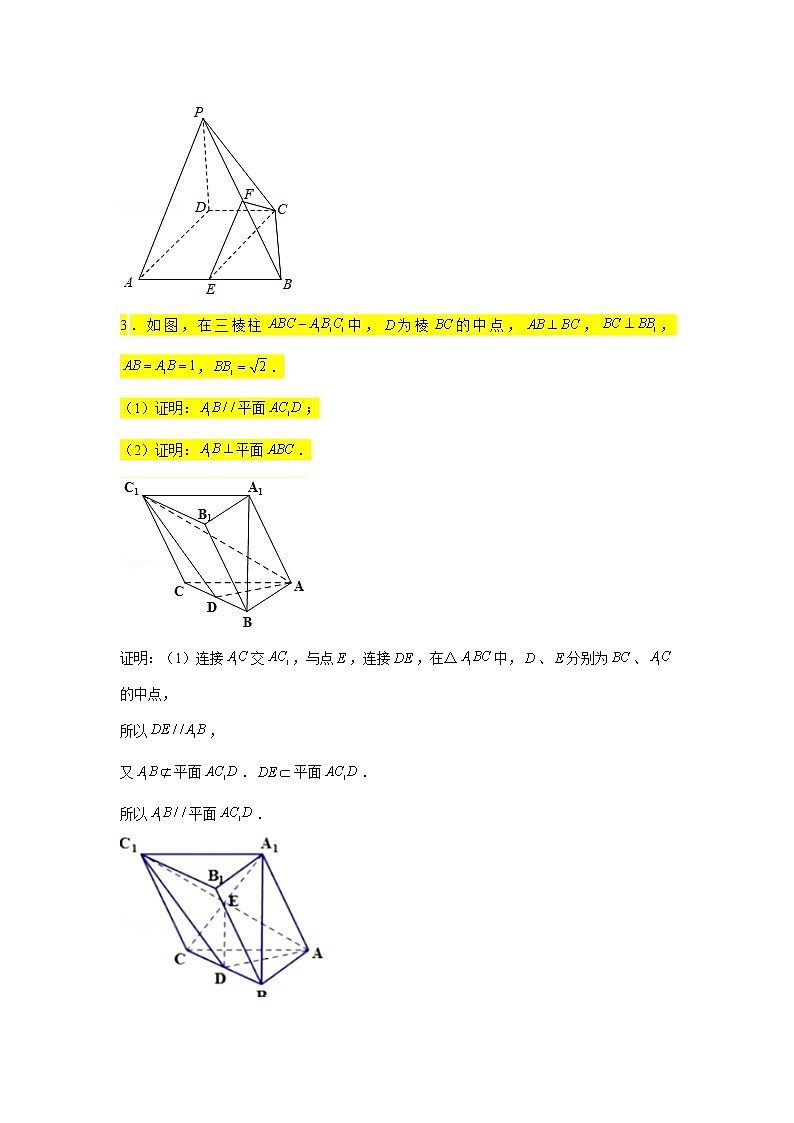
第八章  立体几何专题训练（十）—证明平行、垂直（1）1．如图．在直四棱柱中，，分别，的中点，与交于点．（1）求证：，，，四点共面；（2）若底面是菱形，且，求证：平面．解：（1）连接，因为，分别是，的中点，所以是的中位线，所以，由直棱柱知：，所以四边形为平行四边形，所以，分所以，故，，，四点共面；分，（2）连接，因为直棱柱中平面，平面，所以，因为底面是菱形，所以，又，所以平面，分因为平面，所以，又，，平面，平面，所以平面分2．如图，在四棱锥中，，，，，，，分别为棱，的中点．（1）证明：平面．（2）证明：平面平面．证明：（1）因为，，，所以，所以．因为，，所以平面．（2）因为为棱的中点，所以．因为，所以，因为，所以，所以四边形为平行四边形，所以，所以平面．因为，分别为棱，的中点，所以，所以平面．因为，平面，平面，所以平面平面．3．如图，在三棱柱中，为棱的中点，，，，．（1）证明：平面；（2）证明：平面．证明：（1）连接交，与点，连接，在△中，、分别为、的中点，所以，又平面．平面．所以平面．（2）因为，，，、平面．所以平面，又平面．所以；又因为，得，所以．又，平面，所以平面．4．如图，四面体中，，，平面．为中点，为中点，点在线段上，且．（1）求证：平面；（2）若，是的中点，求证：平面．证明：（1）如图，取的中点为，在上取一点，使得，连结，，，则由，分别为，的中点，可得，且，又为的中点，则，因为，，所以，且，所以，且，故四边形是平行四边形，所以，又平面，平面，所以平面．（2）设为的中点，因为平面，平面，所以，因为，，平面，，所以平面，因为平面，所以，因为点为的中点，，所以点为的中点，因为是的中点，所以，因为，所以是等腰直角三角形，，所以，因为平面，平面，，所以平面．5．如图，在四棱锥中，底面是菱形，平面，，，分别为，的中点．（1）证明：平面；（2）证明：平面．证明：（1）取的中点，连接，．因为，分别为，的中点，所以，．因为底面是菱形，所以，．因为是的中点，所以，，所以，，则四边形为平行四边形，所以．因为平面，平面，所以平面．（2）连接．因为底面是边长为4的菱形，且，所以为等边三角形，因为是的中点，所以，因为平面，平面，所以，因为，平面，，所以平面．6．如图，在三棱台中，面平面，，，点是的中点．（1）求证：平面；（2）求证：．（1）证明：取中点，连接，，又，又平面，平面；（2）证明：取中点，连接，，由，，，四边形是平行四边形，又，，，四边形是菱形，，，，平面，平面，平面，平面，．