北师大九下数学 考点综合专题：圆与其他知识的综合

考点综合专题：圆与其他知识的综合

类型一　圆与三角函数的综合

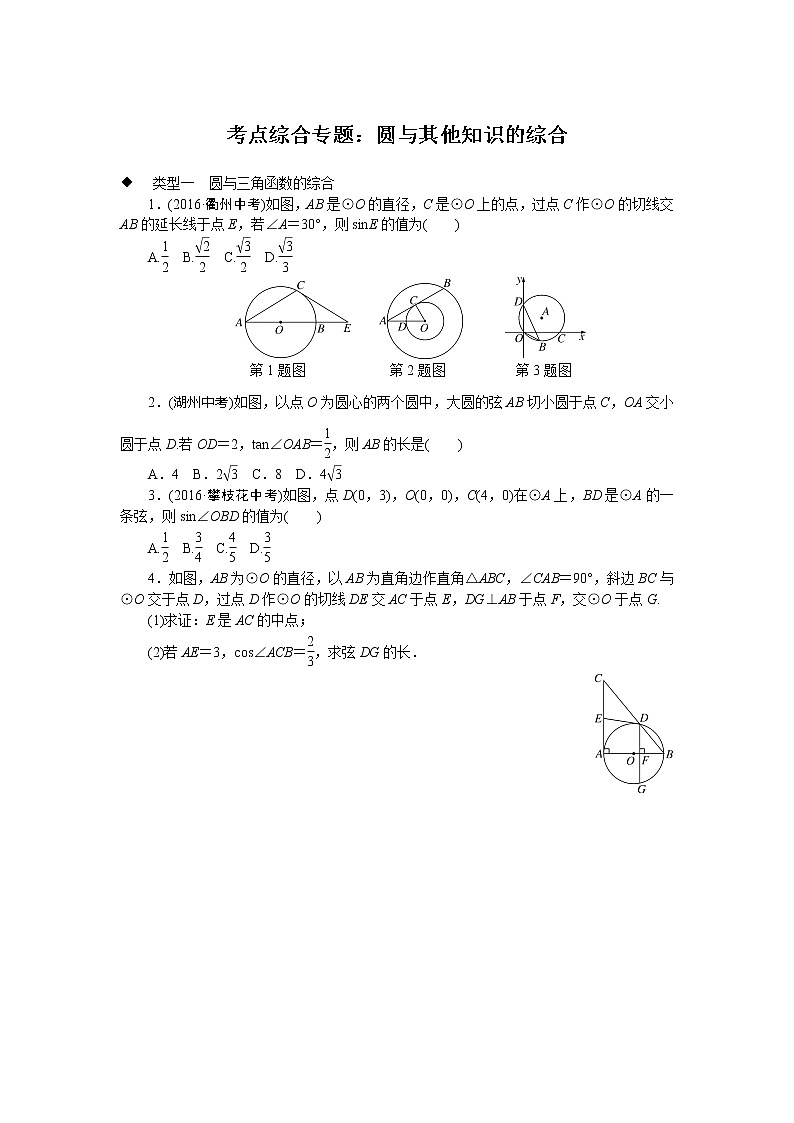
1．(2016·衢州中考)如图，AB是⊙O的直径，C是⊙O上的点，过点C作⊙O的切线交AB的延长线于点E，若∠A＝30°，则sinE的值为(　　)

A.  B.  C.  D.

第1题图            第2题图          第3题图

2．(湖州中考)如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，OA交小圆于点D.若OD＝2，tan∠OAB＝，则AB的长是(　　)

A．4  B．2  C．8  D．4

3．(2016·攀枝花中考)如图，点D(0，3)，O(0，0)，C(4，0)在⊙A上，BD是⊙A的一条弦，则sin∠OBD的值为(　　)

A.  B.  C.  D.

4．如图，AB为⊙O的直径，以AB为直角边作直角△ABC，∠CAB＝90°，斜边BC与⊙O交于点D，过点D作⊙O的切线DE交AC于点E，DG⊥AB于点F，交⊙O于点G.

(1)求证：E是AC的中点；

(2)若AE＝3，cos∠ACB＝，求弦DG的长．

类型二　圆与相似的综合

5．如图，AB是半圆O的直径，D，E是半圆上任意两点，连接AD，DE，AE与BD相交于点C，要使△ADC与△ABD相似，可以添加一个条件．下列添加的条件其中错误的是D

A．∠ACD＝∠DAB  B．AD＝DE

C．AD2＝BD·CD  D．AD·AB＝AC·BD

第5题图              第6题图            第7题图

6．如图，边长为2的正方形ABCD中，P是CD的中点，连接AP并延长，交BC的延长线于点F，作△CPF的外接圆⊙O，连接BP并延长交⊙O于点E，连接EF，则EF的长为D

A.  B.  C.  D.

7．(2016·成都中考)如图，△ABC内接于⊙O，AH⊥BC于点H，若AC＝24，AH＝18，⊙O的半径OC＝13，则AB＝________．

8．(2016·泰州中考)如图，△ABC中，∠ACB＝90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE＝∠ADF.

(1)判断AB与⊙O的位置关系，并说明理由；

(2)若PF∶PC＝1∶2，AF＝5，求PC的长．

类型三　圆与四边形的综合

9．(2016·重庆模拟)如图，⊙O过正方形ABCD的顶点A，B，与CD相切，切点为点E，若正方形ABCD的边长为2，则⊙O的半径为(　　)

A．1  B.  C.  D.

第9题图            第10题图            第11题图

10．(2016·哈尔滨中考)如图，AB为⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足为D，AD交⊙O于点E，连接OC，BE.若AE＝6，OA＝5，则线段DC的长为________．

11．★(2016·淄博中考)如图，⊙O的半径为2，圆心O到直线l的距离为4，有一内角为60°的菱形，当菱形的一边在直线l上，另有两边所在的直线恰好与⊙O相切，此时菱形的边长为____________．

12．(2016·上海中考)如图，⊙O是△ABC的外接圆，＝，点D在边BC上，AE∥BC，AE＝BD.

(1)求证：AD＝CE；

(2)如果点G在线段DC上(不与点D重合)，AG＝AD，求证：四边形AGCE是平行四边形．

类型四　坐标系中的圆(代几综合)

13．如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为(－3，0)，将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为(　　)

A．1  B．1或5  C．3  D．5

第13题图            第14题图

14．(2016·潍坊中考)如图，在平面直角坐标系中，⊙M与x轴相切于点A(8，0)，与y轴分别交于点B(0，4)和点C(0，16)，则圆心M到坐标原点O的距离是(　　)

A．10  B．8  C．4  D．2

15．如图，在Rt△OAB中，OA＝4，AB＝5，点C在OA上，AC＝1，⊙P的圆心P在线段BC上，⊙P与边AB，AO都相切．若反比例函数y＝(k≠0)的图象经过圆心P，则k＝____________.

第15题图        第16题图         第17题图

16．(2016·信阳模拟)如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A，B，C，D分别是“果圆”与坐标轴的交点，抛物线的解析式为y＝x2－2x－3，AB为半圆的直径，则这个“果圆”被y轴截得的弦CD的长为________．

17．★(2016·日照中考)如图，直线y＝－x＋3与x轴、y轴分别交于点A，B，点Q是以C(0，－1)为圆心、1为半径的圆上一动点，过Q点的切线交线段AB于点P，则线段PQ的最小是________．

考点综合专题：圆与其他知识的综合

1．A　2.C

3．D　解析：连接CD.∵点D的坐标为(0，3)，点C的坐标为(4，0)，∴OD＝3，OC＝4.∵∠COD＝90°，∴CD＝＝＝5.∵∠OBD＝∠OCD，∴sin∠OBD＝sin∠OCD＝＝.故选D.

4．(1)证明：连接AD.∵AB为⊙O的直径，∴∠ADB＝90°，∴∠ADC＝90°.∵∠CAB＝90°，∴AC是⊙O的切线．又∵DE与⊙O相切，∴ED＝EA，∴∠EAD＝∠EDA.∵∠C＝90°－∠EAD，∠CDE＝∠ADC－∠ADE＝90°－∠EAD，∴∠C＝∠CDE，∴ED＝EC，∴EA＝EC，即E为AC的中点；

(2)解：由(1)知E为AC的中点，则AC＝2AE＝6.在Rt△ACD中，cos∠ACD＝cos∠ACB＝，∴CD＝AC·cos∠ACB＝6×＝4，∴AD＝＝＝2.∵∠ACB＋∠B＝90°，∠DAB＋∠B＝90°，∴∠ACB＝∠DAB.在Rt△ADF中，AF＝AD·cos∠DAF＝AD·cos∠ACB＝2×＝，∴DF＝＝＝.∵DG⊥AB，∴DG＝2DF＝.

5．D　6.D

7.　解析：作直径AE，连接CE.∴∠ACE＝90°.∵AH⊥BC，∴∠AHB＝90°，∴∠ACE＝∠AHB.∵∠B＝∠E，∴△ABH∽△AEC，∴＝，∴AB＝.∵AC＝24，AH＝18，AE＝2OC＝26，∴AB＝＝.

8．解：(1)AB是⊙O的切线．理由如下：连接DE，CF.∵CD是⊙O的直径，∴∠DEC＝∠DFC＝90°.∵∠ACB＝90°，∴∠DEC＋∠ACE＝180°，∴DE∥AC，∴∠CAE＝∠DEA＝∠DCF.∵∠DFC＝90°，∴∠DCF＋∠CDF＝90°.∵∠ADF＝∠CAE＝∠DCF，∴∠ADF＋∠CDF＝90°，∴∠ADC＝90°，∴CD⊥AD，∴AB是⊙O的切线；

(2)∵∠CPF＝∠CPA，∠PCF＝∠PAC，∴△PCF∽△PAC，∴＝，∴PC2＝PF·PA.设PF＝a，则PC＝2a，∴4a2＝a(a＋5)，∴a＝，∴PC＝2a＝.

9．D　解析：连接OE，OB，延长EO交AB于点F，∴OE⊥CD.∵四边形ABCD是正方形，∴AB∥CD，∴OF⊥AB.设OB＝OE＝R，则OF＝2－R.在Rt△OBF中，BF＝AB＝×2＝1，OB＝R，OF＝2－R，∴R2＝(2－R)2＋12，解得R＝.故选D.

10．4　解析：设OC交BE于点F.∵AB为⊙O的直径，∴AB＝2OA＝10，∠AEB＝90°.∵AD⊥l，∴BE∥CD.∵CD为⊙O的切线，∴OC⊥CD，∴OC⊥BE，∴四边形CDEF为矩形，∴CD＝EF.在Rt△ABE中，BE＝＝＝8.∵OF⊥BE，∴BF＝EF＝BE＝4，∴CD＝4.

11．4或或　解析：第一种情况：如图①，过点O作直线l的垂线，交AD于E，交BC于F，过点A作AG⊥直线l于点G，由题意得EF＝2＋4＝6，四边形AGFE为矩形，∴AG＝EF＝6.在Rt△ABG中，AB＝＝＝4；

第二种情况：如图②，过点O作OE⊥l于点E，过点D作DF⊥l于点F，则OE＝4，DF＝2.在Rt△DCF中，DC＝＝DF＝；

第三种情况：如图③，过点O作EF垂直于BA延长线于点E，交CD于点F，过点A作AG⊥CD于点G，则AG＝EF＝4.在Rt△AFG中，AF＝＝AG＝.故答案为4或或.

12．证明：(1)在⊙O中，∵＝，∴AB＝AC，∴∠B＝∠ACB.∵AE∥BC，∴∠EAC＝∠ACB，∴∠B＝∠EAC.在△ABD和△CAE中，∴△ABD≌△CAE(SAS)，∴AD＝CE；

(2)连接AO并延长，交边BC于点H.∵＝，OA为半径，∴AH⊥BC，∴BH＝CH.∵AD＝AG，∴DH＝GH，∴BH－DH＝CH－GH，即BD＝CG.∵BD＝AE，∴CG＝AE.∵CG∥AE，∴四边形AGCE是平行四边形．

13．B

14．D　解析：连接BM，OM，AM，过点M作MH⊥BC于点H.∵⊙M与x轴相切于点A(8，0)，∴AM⊥OA，OA＝8，∴∠OAM＝∠MHO＝∠HOA＝90°，∴四边形OAMH是矩形，∴AM＝OH.∵点B的坐标为(0，4)，点C的坐标为(0，16)，∴OB＝4，OC＝16，∴BC＝12.∵MH⊥BC，∴CH＝BH＝BC＝×12＝6，∴OH＝OB＋BH＝4＋6＝10，∴AM＝10.在Rt△AOM中，OM＝＝＝2.故选D.

15.　解析：在Rt△OAB中，OA＝4，AB＝5，∴OB＝3.设⊙P与边AB，AO分别相切于点F，E，连接PE，PF，AP，则PF⊥AB，PE⊥OA，PE＝PF.∵OA＝4，OB＝3，AC＝1，∴OC＝OA－AC＝3＝OB.又∵∠AOB＝90°，∴∠OBC＝∠OCB＝45°，∴∠EPC＝45°＝∠ECP，∴PE＝CE.∵S△ABC＝S△ABP＋S△ACP，∴AC·OB＝AB·PF＋AC·PE.∴×1×3＝×5×PE＋×1×PE，解得PE＝.∴CE＝PE＝，∴OE＝OC－CE＝3－＝，∴点P的坐标为.∵反比例函数y＝(k≠0)的图象经过点P，∴k＝×＝.

16．3＋　解析：连接AC，BC.∵抛物线的解析式为y＝x2－2x－3，∴点D的坐标为(0，－3)，∴OD＝3.设y＝0，则0＝x2－2x－3，解得x＝－1或3，∴点A的坐标为(－1，0)，点B的坐标为(3，0)，∴AO＝1，BO＝3.∵AB为半圆的直径，∴∠ACB＝90°.又∵CO⊥AB，易证△AOC∽△COB，∴CO2＝AO·BO＝3，∴CO＝，∴CD＝OD＋CO＝3＋.

17.　解析：过点C作CP⊥AB于点P，过点P作⊙C的切线PQ，切点为Q，此时PQ最小，连接CQ，AC，如图所示．直线AB的解析式为y＝－x＋3，∴点A的坐标为(4，0)，点B的坐标为(0，3)，∴OA＝4，OB＝3，∴AB＝＝＝5.∵点C的坐标为(0，－1)，∴OC＝1，∴S△ABC＝S△AOB＋S△AOC＝×4×3＋×4×1＝8.又∵S△ABC＝AB·CP，∴CP＝.∵PQ为⊙C的切线，∴∠CQP＝90°.在Rt△CQP中，PQ＝＝＝.