(通用版)中考数学总复习随堂练习10《一次函数》(含答案)
展开专题10一次函数
A组基础巩固
1.直线y=(3-π)x经过的象限是(D)
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
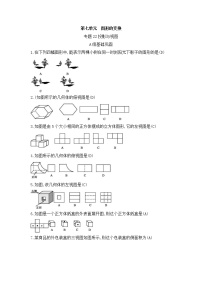
2.已知一次函数y=kx+b,若k+b=0,则该函数的图象可能是(A)
3.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=kx+k的图象经过的象限为(A)
A.第二、三、四象限 B.第一、二、四象限
C.第一、三、四象限 D.第一、二、三象限
4.已知直线y=ax+b(a≠0)经过点A(-3,0)和点B(0,2),那么关于x的方程ax+b=0的解是(A)
A.x=-3 B.x=-1 C.x=0 D.x=2
5.把直线y=-x-1向y轴正方向平移4个单位,得到的直线与y轴的交点坐标为(0,3).
6.如图,直线x=2与y=x+a的交点A在第四象限,则a的取值范围是a<-2.
7.如图,长方形ABCD中,点P沿着四边按B→C→D→A方向,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后恢复原速匀速运动.在运动过程中,△ABP的面积S与运动时间t的函数关系如图所示.
(1)求长方形的长和宽;
(2)求m,a,b的值;
(3)当P点在AD边上时,求S与t的函数解析式.
解 (1)从图象可知,当6≤t≤8时,△ABP面积不变,
即6≤t≤8时,点P从点C运动到点D,且这时速度为每秒2个单位,∴CD=2×(8-6)=4,∴AB=CD=4.
当t=6时(点P运动到点C),S△ABP=16,∴AB·BC=16,
∴BC=8,故长方形的长为8,宽为4.
(2)当t=a时,S△ABP=AB·BP=2BP=8,即点P此时在BC的中点处,
∴PC=BC=×8=4,
∴2(6-a)=4,∴a=4.
∵BP=PC=4,∴m===1.
当t=b时,S△ABP=AB·AP=4,
∴×4×AP=4,AP=2,=2,∴b=13-2=11.
(3)当8≤t≤11时,S关于t的函数图象是过点(8,16),(11,4)的一条直线,可设S=kt+b,
∴∴
∴S=-4t+48(8≤t≤11).
同理可求当11≤t≤13时S关于t的函数解析式:S=-2t+26(11≤t≤13).
B组能力提升
1.复习课中,教师给出关于x的函数y=-2mx+m-1(m≠0).学生们在独立思考后,给出了5条关于这个函数的结论:
①此函数是一次函数,但不可能是正比例函数;
②函数的值y随着自变量x的增大而减小;
③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x-3及y轴围成的面积必小于0.5.
以上5个结论中正确的有(D)个.
A.4 B.3 C.2 D.0
2.若A(x1,y1),B(x2,y2)是一次函数y=ax+x-2图象上的不同的两点,记m=(x1-x2)(y1-y2),则当m<0时,a的取值范围是(C)
A.a<0 B.a>0 C.a<-1 D.a>-1
3.如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为y=x.
4.波波和爸爸两人以相同路线从家出发,步行前往公园.图中OA,BC分别表示爸爸和波波所走的路程y(单位:米)与步行的时间x(单位:分)的函数图象,已知爸爸从家步行到公园所花的时间比波波的2倍还多10分钟.则在步行过程中,他们父子俩相距的最远路程是1 200米.
5.如图1,某商场有一双向运行的自动扶梯,扶梯上行和下行的速度保持不变且相同,甲、乙两人同时站上了此扶梯的上行端和下行端,甲站在上行扶梯的同时又以0.8 m/s的速度往上跑,乙站在下行扶梯后则站立不动随扶梯下行,两人在途中相遇,甲到达扶梯顶端后立即乘坐下行扶梯,同时以0.8 m/s的速度往下跑,而乙到达底端后则在原地等候甲.图2中线段OB,AB分别表示甲、乙两人在乘坐扶梯过程中,离扶梯底端的路程y(单位:m)与所用时间x(单位:s)之间的部分函数关系,结合图象解答下列问题:
(1)点B的坐标是 ;
(2)求AB所在直线的函数关系式;
(3)乙到达扶梯底端后,还需等待多长时间,甲才到达扶梯底端?
解 (1)(7.5,18)
(2)设直线AB的函数关系式为y=kx+b,
点A,B坐标分别为(0,30),(7.5,18),代入y=kx+b,
得解得
故AB所在直线的函数关系式为y=-1.6x+30.
(3)30×2÷(1.6+0.8)-30÷1.6=60÷2.4-18.75=25-18.75=6.25(s).故乙到达扶梯底端后,还需等待6.25 s,甲才到达扶梯底端.
6.在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(0,4),点M是线段AB上任意一点(A,B两点除外).
(1)求直线AB的解析式.
(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由.
(3)当点M把线段AB分成的两部分的比为1∶3时,请求出点M的坐标.
解 (1)设直线AB的解析式为y=kx+b,
由题意可得解得
故AB的解析式为y=-x+4.
(2)不发生变化.
理由如下:设M点的坐标为(x,-x+4),当点M在AB上运动时,MD=|x|=x,MC=|-x+4|=-x+4,
四边形OCMD的周长=2(MD+MC)=2[x+(-x+4)]=8,
即四边形OCMD的周长不发生变化.
(3)∵DM∥x轴,∴=.
①当BM∶MA=1∶3时,==,即=,DM=1,则点M的横坐标为1,此时纵坐标=-x+4=-1+4=3,M(1,3).
②当BM∶MA=3∶1时,==,即=,DM=3,则点M的横坐标为3,此时纵坐标=-x+4=-3+4=1,M(3,1).
综上可知点M的坐标为(1,3)或(3,1).
(通用版)中考数学总复习随堂练习26《概率》(含答案): 这是一份(通用版)中考数学总复习随堂练习26《概率》(含答案),共3页。试卷主要包含了下列事件是必然事件的是,下列说法正确的是,01,乙组数据的方差=0等内容,欢迎下载使用。
(通用版)中考数学总复习随堂练习25《统计》(含答案): 这是一份(通用版)中考数学总复习随堂练习25《统计》(含答案),共4页。试卷主要包含了2+88×0等内容,欢迎下载使用。
(通用版)中考数学总复习随堂练习24《相似变换》(含答案): 这是一份(通用版)中考数学总复习随堂练习24《相似变换》(含答案),共3页。