人教版七下数学 思想方法专题：相交线与平行线中的思想方法

这是一份人教版七下数学 思想方法专题：相交线与平行线中的思想方法，共6页。

eq \a\vs4\al(◆)类型一 方程思想
1．如图，直线AB，CD相交于点O，∠AOC＝60°，OE把∠BOD分成两部分，且∠BOE∶∠EOD＝1∶2，则∠AOE的度数为( )
A．180° B．160° C．140° D．120°
第1题图 第2题图
2．(2017·无棣县期末)如图，直线AB，CD相交于点O，OE平分∠BOD，OF平分∠COB，∠AOD∶∠EOD＝4∶1，则∠AOF的度数为________．
3．如图，已知FC∥AB∥DE，∠α∶∠D∶∠B＝2∶3∶4.求∠α，∠D，∠B的度数．
4．(2017·启东市期末)如图，AD∥BC，BE平分∠ABC交AD于点E，BD平分∠EBC.
(1)若∠DBC＝30°，求∠A的度数；
(2)若点F在线段AE上，且7∠DBC－2∠ABF＝180°，请问图中是否存在与∠DFB相等的角？若存在，请写出这个角，并说明理由；若不存在，请说明理由．
eq \a\vs4\al(◆)类型二 分类讨论思想
5．若∠α与∠β的两边分别平行，∠α比∠β的3倍少36°，则∠α的度数是( )
A．18° B．126°
C．18°或126° D．以上都不对
6．(2017·玄武区期末)在直线MN上取一点P，过点P作射线PA、PB.若PA⊥PB，当∠MPA＝40°，则∠NPB的度数是________________．
7．(2017·江干区一模)一副直角三角尺按如图①所示方式叠放，现将含45°角的三角尺ADE固定不动，将含30°角的三角尺ABC绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行．如图②，当∠BAD＝15°时，BC∥DE，则∠BAD(0°＜∠BAD＜180°)其他所有可能符合条件的度数为________________________________________________________________________．
8．如图，已知直线l1∥l2，直线l3交l1于C点，交l2于D点，P是线段CD上的一个动点．当P在直线CD上运动时，请你探究∠1，∠2，∠3之间的关系．
eq \a\vs4\al(◆)类型三 (转化思想)利用平移进行转化求图形的周长或面积
9．如图，直角三角形ABC的周长为100，在其内部有6个小直角三角形，则6个小直角三角形的周长之和为________．
第9题图
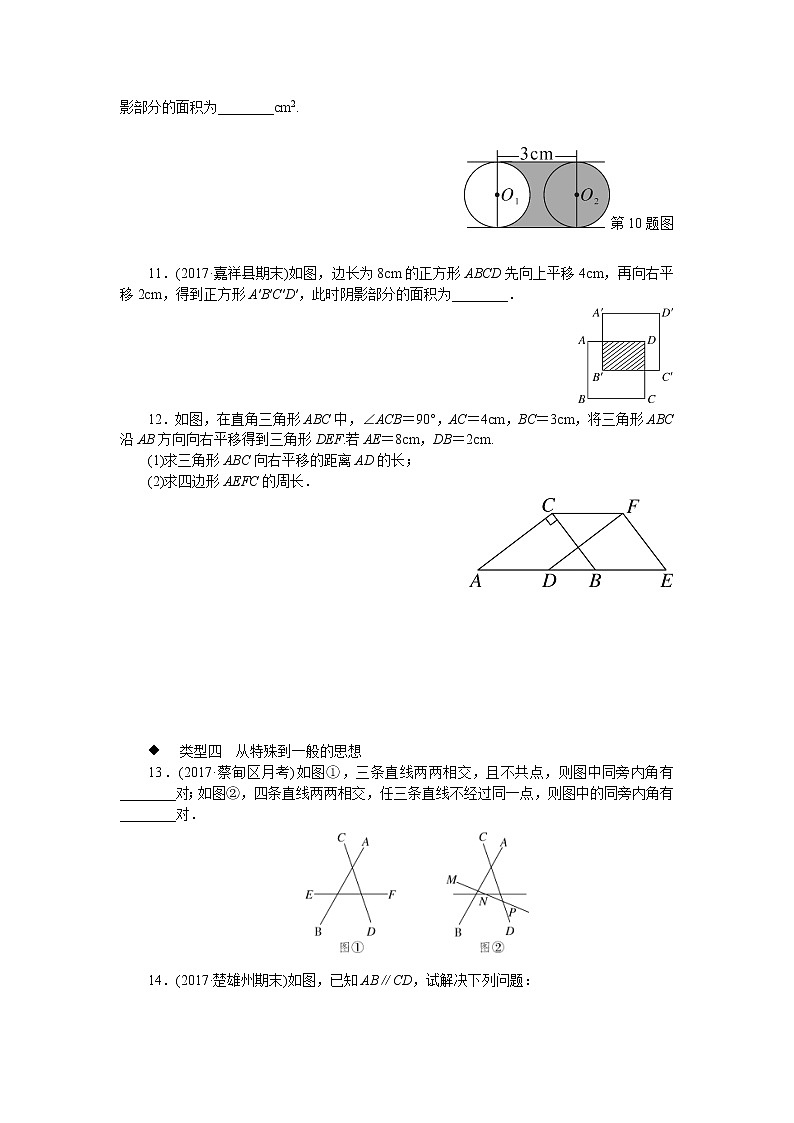
10．(2017·惠山区期中)如图，直径为2cm的圆O1平移3cm到圆O2的位置，则图中阴影部分的面积为________cm2.
第10题图
11．(2017·嘉祥县期末)如图，边长为8cm的正方形ABCD先向上平移4cm，再向右平移2cm，得到正方形A′B′C′D′，此时阴影部分的面积为________．
12．如图，在直角三角形ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm，将三角形ABC沿AB方向向右平移得到三角形DEF.若AE＝8cm，DB＝2cm.
(1)求三角形ABC向右平移的距离AD的长；
(2)求四边形AEFC的周长．
eq \a\vs4\al(◆)类型四 从特殊到一般的思想
13．(2017·蔡甸区月考)如图①，三条直线两两相交，且不共点，则图中同旁内角有________对；如图②，四条直线两两相交，任三条直线不经过同一点，则图中的同旁内角有________对．
14．(2017·楚雄州期末)如图，已知AB∥CD，试解决下列问题：
(1)∠1＋∠2＝________；
(2)∠1＋∠2＋∠3＝________；
(3)∠1＋∠2＋∠3＋∠4＝________；
(4)试探究∠1＋∠2＋∠3＋∠4＋…＋∠n＝____________．
15．(2017·丛台区期末)如图，AB∥CD，∠ABE与∠CDE两个角的平分线相交于点F.
(1)如图①，若∠E＝80°，求∠BFD的度数；
(2)如图②，∠ABM＝eq \f(1,3)∠ABF，∠CDM＝eq \f(1,3)∠CDF，写出∠M与∠E之间的数量关系，并证明你的结论；
(3)若∠ABM＝eq \f(1,n)∠ABF，∠CDM＝eq \f(1,n)∠CDF，设∠E＝m°，直接用含有n，m°的代数式表示∠M＝________．
参考答案与解析
1．B 2.120°
3．解：设∠α＝2x°，则∠D＝3x°，∠B＝4x°.∵FC∥AB∥DE，∴∠2＋∠B＝180°，∠1＋∠D＝180°，∴∠2＝180°－∠B＝180°－4x°，∠1＝180°－∠D＝180°－3x°.又∵∠1＋∠2＋∠α＝180°，∴(180－3x)＋(180－4x)＋2x＝180，解得x＝36，∴∠α＝2x°＝72°，∠D＝3x°＝108°，∠B＝4x°＝144°.
4．解：(1)∵BD平分∠EBC，∠DBC＝30°，∴∠EBC＝2∠DBC＝60°.∵BE平分∠ABC，∴∠ABC＝2∠EBC＝120°.∵AD∥BC，∴∠A＋∠ABC＝180°，∴∠A＝60°.
(2)存在∠DFB＝∠DBF.设∠DBC＝x°，则∠EBC＝2x°，∠ABC＝2∠EBC＝4x°.∵7∠DBC－2∠ABF＝180°，∴7x°－2∠ABF＝180°，∴∠ABF＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7,2)x－90))°，∴∠CBF＝∠ABC－∠ABF＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x＋90))°，∠DBF＝∠CBF－∠DBC＝eq \b\lc\(\rc\)(\a\vs4\al\c1(90－\f(1,2)x))°.∵AD∥BC，∴∠DFB＋∠CBF＝180°，∴∠DFB＝eq \b\lc\(\rc\)(\a\vs4\al\c1(90－\f(1,2)x))°，∴∠DFB＝∠DBF.
5．C 解析：∵∠α与∠β的两边分别平行，∴∠α与∠β相等或互补．设∠α＝x°，∵∠α比∠β的3倍少36°，∴若∠α与∠β相等，则x＝3x－36，解得x＝18.若∠α与∠β互补，则x＝3(180－x)－36，解得x＝126，∴∠α的度数是18°或126°.故选C.
6．50°或130° 解析：分两种情况：(1)如图①，∵PA⊥PB，∠MPA＝40°，∴∠NPB＝180°－90°－40°＝50°；(2)如图②，∵PA⊥PB，∠MPA＝40°，∴∠MPB＝50°，∴∠NPB＝180°－50°＝130°.综上所述，∠NPB的度数是50°或130°.
7．45°，60°，105°或135° 解析：分以下四种情况：(1)AC∥DE，如图①，此时点B在AE上，∴∠BAD＝45°；(2)AB∥DE，如图②，∴∠EAB＝∠E＝90°，∴∠BAD＝∠BAE＋∠EAD＝135°；(3)BC∥AD，如图③，∴∠BAD＝∠B＝60°；(4)BC∥AE，如图④，∴∠BAE＝∠B＝60°，∴∠BAD＝∠BAE＋∠EAD＝105°.综上所述，∠BAD其他所有可能符合条件的度数为45°，60°，105°，135°.
8．解：分以下三种情况：(1)当点P在线段CD上运动时，如图①.过点P向左作PE∥l.∵l1∥l2，∴PE∥l2.∴∠APE＝∠1，∠BPE＝∠3，∴∠2＝∠APE＋∠BPE＝∠1＋∠3.
(2)当点P在l1上方运动时，如图②，过点P向左作PF∥l2.∵l2∥l1，∴PF∥l1.∴∠FPB＝∠3，∠FPA＝∠1，∴∠2＝∠FPB－∠FPA＝∠3－∠1.
(3)当点P在l2下方运动时，如图③，过点P向左作PM∥l2.∵l1∥l2，∴PM∥l1，∴∠APM＝∠1，∠BPM＝∠3，∴∠2＝∠APM－∠BPM＝∠1－∠3.
9．100 10.6 11.24cm2
12．解：(1)∵三角形ABC沿AB方向向右平移得到三角形DEF，∴AD＝BE＝CF，EF＝BC＝3cm.∵AE＝8cm，DB＝2cm，∴AD＝BE＝CF＝eq \f(8－2,2)＝3(cm)．
(2)四边形AEFC的周长为AE＋EF＋CF＋AC＝8＋3＋3＋4＝18(cm)．
13．6 24
14．(1)180° (2)360°
(3)540° 解析：过点E，F向右作EG，FH平行于AB.∵AB∥CD，∴AB∥EG∥FH∥CD，∴∠1＋∠AEG＝180°，∠GEF＋∠EFH＝180°，∠HFC＋∠4＝180°，∴∠1＋∠2＋∠3＋∠4＝540°.
(4)180°(n－1) 解析：易知有n个角，需作(n－2)条辅助线，运用(n－1)次两条直线平行，同旁内角互补．即可得到n个角的和是180°(n－1)．
15．解：(1)如图，过点E向左作EG∥AB，过点F向右作FH∥AB.∵AB∥CD，∴EG∥AB∥FH∥CD，∴∠ABF＝∠BFH，∠CDF＝∠DFH，∠ABE＋∠BEG＝180°，∠GED＋∠CDE＝180°，∴∠ABE＋∠BEG＋∠GED＋∠CDE＝360°.∵∠BEG＋∠DEG＝∠BED＝80°，∴∠ABE＋∠CDE＝280°.∵∠ABE和∠CDE的平分线相交于F，∴∠ABF＝eq \f(1,2)∠ABE，∠CDF＝eq \f(1,2)∠CDE，∴∠ABF＋∠CDF＝eq \f(1,2)(∠ABE＋∠CDE)＝140°，∴∠BFD＝∠BFH＋∠DFH＝∠ABF＋∠CDF＝140°.
(2)∵∠ABM＝eq \f(1,3)∠ABF，∠CDM＝eq \f(1,3)∠CDF，∴∠ABF＝3∠ABM，∠CDF＝3∠CDM.∵∠ABE与∠CDE两个角的平分线相交于点F，∴∠ABE＝6∠ABM，∠CDE＝6∠CDM，由(1)知∠ABE＋∠E＋∠CDE＝360°，∴6∠ABM＋6∠CDM＋∠E＝360°.过点M向右作MN∥AB，易证∠M＝∠ABM＋∠CDM，∴6∠M＋∠E＝360°.
(3)eq \f(360°－m°,2n) 解析：由(2)可得，2n∠ABM＋2n∠CDM＋∠E＝360°，∠M＝∠ABM＋∠CDM，∴∠M＝eq \f(360°－m°,2n).故答案为eq \f(360°－m°,2n).