




期末检测押题卷(五)-2021-2022学年七年级数学下学期期末专项复习(人教版)
展开
期末检测押题卷(五)
(全卷共三个大题,共23题,共8页;满分120分,考试用时120分钟)
注意事项:
1. 本卷为试题卷,考生必须在答题卡上解题做答.答案应写在答题卡的相应位置上,在试题卷、草稿纸上作答无效。
2. 考试结束后,请将试卷和答题卡一并交回.
一、 选择题(本大题共8小题,每小题4分,共32分,每小题正确的选项只用一个)
1. 如图,雷达探测器发现了A,B,C,D,E,F六个目标.目标C,F的位置分别表示为C(6,120°),F(5,210°),按照此方法表示目标A,B,D,E的位置时,其中表示正确的是( )
A.A(4,30°) B.B(1,90°) C.D( 4,240°) D.E(3,60°)
【答案】C
【解析】
解:按已知可得,表示一个点,横坐标是自内向外的环数,纵坐标是所在列的度数,
由题意可知、、、的坐标可表示为:(5,30°),故A不正确;
(2,90°),故B不正确;
(4,240°),故C正确;
(3,300°),故D不正确.
故选择:C.
2. 下列方程中,二元一次方程共有 ( )
3x+6=2x xy=2 y- =4 ④10x- =2y
A.1 个 B.2 个 C.3 个 D.4 个
【答案】A
【解析】
①3x+6=2x是一元一次方程,故本小题错误;
②xy=2是二元二次方程,故本小题错误;
③y−=4是一元一次方程,故本小题错误;
④10x-=2y是二元一次方程,故本小题正确.
故答案选A.
3. 下列各数中,是无理数的是( )
A. B. C. D.
【答案】D
【解析】
解:A.,是有理数,故选项错误;
B.,是有理数,故选项错误;
C.,是有理数,故选项错误;
D.,是无理数,故选项正确;
故选:D.
4. 如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠3+∠8=180°;③∠4=∠5;④∠6+∠7=180°.其中,能够判断a∥b的是( )
A. B. C. D.
【答案】D
【解析】
①∵∠1=∠2,∴a∥b,故本小题正确;
②∵∠3+∠8=180°,∠3+∠7=180°,∠4+∠8=180°,
∴∠4+∠7=180°,
∴a∥b,故本小题正确;
③∵∠4=∠5,∴a∥b,故本小题正确;
④∵∠6+∠7=180°,∠6+∠2=180°,
∴∠7=∠2,
∴a∥b,故本小题正确.
故选D.
5. 元代数学家朱世杰撰写的《四元玉鉴》中记载了一个问题,大意是:用九百九十九文钱共买了一千个甜果和苦果,其中四文钱可买苦果七个,十一文钱可买甜果九个,问甜果、苦果各几个?设买了甜果个,苦果个,根据题意可列方程组( )
A. B.
C. D.
【答案】B
【解析】
解:由题意得:
,
故选B.
6. 下列命题是假命题的是( )
A.两直线平行,内错角相等 B.相等的角是对顶角
C.所有的直角都是相等的 D.若a=b,则a-1=b-1
【答案】B
【解析】
A,两直线平行,内错角相等,是真命题;
B,相等的角不一定是对顶角,是假命题;
C,所有的直角都是相等的,是真命题;
D,若a=b,则a-1=b-1是等式的性质,是真命题.
故答案选:B.
7. 关于x的一元一次不等式≤﹣2的解集为x≥4,则m的值为( )
A.14 B.7 C.﹣2 D.2
【答案】D
【解析】
≤﹣2,
m﹣2x≤﹣6,
﹣2x≤﹣m﹣6,
x≥m+3,
∵关于x的一元一次不等式≤﹣2的解集为x≥4,
∴m+3=4,解得m=2.
故选D.
8. 下列调查中,适宜采用普查方式的是( )
A.了解一批灯泡的使用寿命 B.了解外地游客对天柱山的印象
C.了解本班同学早餐是否有喝牛奶的习惯 D.了解我国初中学生的视力情况
【答案】C
【解析】
A.了解一批灯泡的寿命适宜采用抽样调查方式,故A选项错误;
B. 了解外地游客对天柱山的印象适宜采用抽样调查方式,故B选项错误;
C. 了解本班同学早餐是否有喝牛奶的习惯适宜采用普查方式, 故C选项正确;
D. 了解我国初中学生的视力情况适宜采用抽样调查方式,故D选项错误;
故选C.
二、 填空题(本大题共6小题,每小题3分,共18分)
9. 若式子∣a-4∣+( b +5)2=0,则点(a, b)在第________象限.
【答案】四
【解析】
解:∵,
∴,,
∴,;
∴点(4,)在第四象限;
故答案为:四.
10.下列说法:①如果两个三角形全等,那么这两个三角形一定成轴对称;②数轴上的点和实数一一对应;③若,则;④两个无理数的和一定为无理数;⑤精确到十分位;⑥如果一个数的算术平方根等于它本身,那么这个数是0.其中正确的说法有______.(填序号)
【答案】②
【解析】
解:①如果两个三角形关于某直线对称,那么这两个三角形一定全等,所以错误;
②数轴上的点和实数一一对应,本项说法正确;
③若,则也成立,所以错误;
④两个无理数的和不一定为无理数,比如:,所以错误;
⑤,所以精确到十分位不正确;
⑥算术平方根等于本身的是0,1,所以错误;
考查平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键.
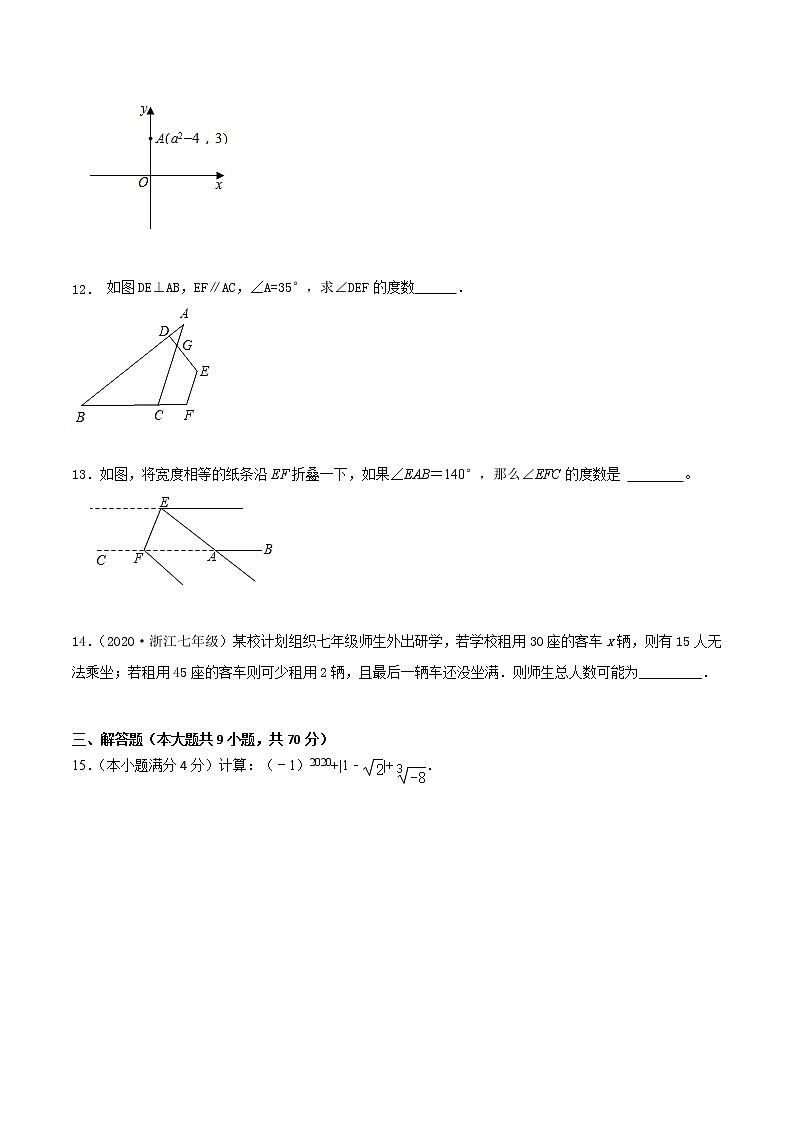
11.如图,在平面直角坐标系xOy中,点A(a2﹣4,3)在y轴上,点B在x轴上,且横坐标为a,则点B的坐标为 .
【答案】(2,0)和(﹣2,0).
【解答】解:∵点A(a2﹣4,3)在y轴上,
∴a2﹣4=0,
解得:a=2或﹣2,
∵点B在x轴上,且横坐标为a,
∴点B的坐标为:(2,0)和(﹣2,0).
故答案为:(2,0)和(﹣2,0).
12. 如图DE⊥AB,EF∥AC,∠A=35°,求∠DEF的度数 .
【答案】125°.
【解析】
解:∵DE⊥AB,
∴∠ADE=90°,
∵∠DGC是△ADG的外角,∠A=35°,
∴∠DGC=∠A+∠ADG=35°+90°=125°,
∵EF∥AC,
∴∠DEF=∠DGC=125°.
13.如图,将宽度相等的纸条沿EF折叠一下,如果∠EAB=140°,那么∠EFC的度数是 。
【答案】110°
【解答】解:如图,
∵将一个宽度相等的纸条按右图所示折叠,
∴∠3=∠4,
∵a∥b,
∴∠1=∠3+∠4,∠2+∠3=180°,
∴2∠3=140°,
∴∠3=70°,
∴∠2=180°﹣70°=110°,即∠EFC=110°.
14.(2020·浙江七年级)某校计划组织七年级师生外出研学,若学校租用30座的客车x辆,则有15人无法乘坐;若租用45座的客车则可少租用2辆,且最后一辆车还没坐满.则师生总人数可能为_________.
【答案】 255人或285人
【解析】
解:由题意可得,
乘坐最后一辆45座客车的人数是:30x+15-45(x-3)=-15x+150,
∵最后一辆车还没坐满,
∴0<-15x+150<45,
解得:7<x<10,
x的取值可能为8或9,
30×8+15=255,30×9+15=285,
∴总人数可能为255人或285人,
故答案为: 255人或285人.
三、 解答题(本大题共9小题,共70分)
15.(本小题满分4分)计算:(﹣1)2020+|1﹣|+.
【答案】解:原式=1+﹣1﹣2
=﹣2.
【解析】直接利用立方根的性质以及绝对值的性质分别化简得出答案.
16.(本小题满分8分)(2020·哈尔滨市第六十九中学校七年级月考)已知是关于x,y的二元一次方程组的解,求a+b的值.
【答案】
解:将代入二元一次方程组,得
,
解得:,
∴a+b的值为:.
【解析】
将代入二元一次方程组求解即可.
17. (本小题满分10分)解不等式(组):
(1). (2)
【答案】
(1)
去分母得到
移项得到
化简得到
系数化为1得x>-.
(2)
去括号得到
移项得
化简,系数化为1得,
去分母得到
移项得到
化简,系数化为1得
故答案为-1<x≤2
【解析】
(1)先去分母,再移项,系数化为1,即可得到答案.
(2)先分别计算着两个不等式,再求不等式组的解.
18.(本小题满分6分)如图,已知AC∥ED,ED∥GF,∠BDF=90°.
(1)若∠ABD=150°,求∠GFD的度数;
(2)若∠ABD=θ,求∠GFD-∠CBD的度数.
【答案】
解:(1)∵AC∥ED,
∴∠ABD+∠BDE=180°,
∵∠ABD=150°,
∴∠BDE=30°,
∵∠BDF=90°,
∴∠EDF=60°,
∵ED∥GF,
∴∠EDF+∠F=180°,
∴∠F=120°;
(2)∵AC∥ED,
∴∠ABD+∠BDE=180°,
∵∠ABD=θ,
∴∠BDE=180°-θ,
∵∠BDF=90°,
∴∠EDF=90°-(180°-θ)=θ-90°,
∵ED∥GF,
∴∠EDF+∠F=180°,
∴∠F=180°-(θ-90°)=270°-θ,
∵∠ABD=θ,
∴∠CBD=180°-θ,
∴∠GFD-∠CBD=270°-θ-180°+θ=90°.
【解析】
(1)根据平行线的性质可得∠ABD+∠BDE=180°,进而可得∠BDE=30°,然后再计算出∠EDF的度数,再根据平行线的性质可得∠EDF+∠F=180°,进而可得∠GFD的度数;
(2)与(1)类似,表示出∠F的度数,再表示出∠CBD的度数,再求差即可.
19.(本小题满分8分)某校有1800名学生.为了解全校学生的上学方式,该校数学兴趣小组经历了以下数据处理的一般过程:收集数据:在全校随机抽取120名学生进行抽样调查;整理、描述数据:整理样本数据,得到频数分布表和统计图;分析数据:根据抽样调查结果,将估计出的全校1800名学生上学方式的情况绘制成条形统计图;
某校120名学生上学方式频数分布表
上学方式 | 频数 |
乘公共交通工具 | 40 |
步行 | 12 |
骑自行车 | a |
乘私家车 | 24 |
其它 | 8 |
合计 | 120 |
得出结论:该校数学兴趣小组结合调查获取的信息,提出了一些建议.如:乘公共交通工具上学的人数较多,学校附近应建公共交通站台.
回答问题:
(1)如果120名学生全部在七年级抽取,是否合理? (填“是”或“否”);频数分布表中a= .
(2)计算出扇形统计图中“乘公共交通工具”部分的圆心角为多少度?
(3)补全条形统计图.
(4)请你结合上述统计的全过程,再提出一条合理化建议.
【答案】解:(1)由题意可知,如果120名学生全部在七年级抽取,否合理;
a=120﹣40﹣12﹣24﹣8=36,
故答案为:否,36;
(2)扇形统计图中“乘公共交通工具”部分的圆心角的度数是:360°×=120°;
(3)骑自行车的有:1800×30%=540(人),
补全的条形统计图如右图所示;
(4)骑自行车上学的学生较多,建议学校合理安排自行车停放场地.
【解析】(1)根据随机抽样的特点,可知如果120名学生全部在七年级抽取不合理,然后根据频数分布表中的数据,可以计算出a的值;
(2)根据频数分布表中的数据,可以计算出扇形统计图中“乘公共交通工具”部分的圆心角的度数;
(3)根据统计图中的数据,可以计算出骑自行车的人数,从而可以将条形统计图补充完整;
(4)本题答案不唯一,提出的建议只要合理即可.
20.(本小题满分6分)(2020·黑龙江七年级期末)疫情爆发,物资紧缺,一医药集团主动担当作为,紧急投产口罩生产线,每天生产医用防护口罩或者医用外科口罩.已知2天生产医用防护口罩、1天生产医用外科口罩,可生产两种口罩共8万只;若1天生产医用防护口罩、3天生产医用外科口罩,可生产两种口罩共9万只.
(1)求平均每天生产医用防护口罩和医用外科口罩各多少万只?
(2)该集团现接到需要180万只口罩的订单,要求生产时间不能超过70天,则工厂至少能生产多少万只医用防护口罩?
【答案】
(1)设日平均生产医用防护口罩x万只,日平均生产医用外科口罩y万只,
由题意得,
解得:,
答:日平均生产医用防护口罩3万只,日平均生产医用外科口罩2万只.
(2)工厂生产n万只医用防护口罩,则生产(180-n)万只医用外科口罩,
由题意得:
解得n≥120,
∵n为正整数,
∴n的最小值为120.
答:工厂至少能生产120万只医用防护口罩.
【解析】
(1)设日平均生产医用防护口罩x万只,日平均生产医用外科口罩y万只,根据题意,列出二元一次方程组,解之即可解答;
(2)工厂生产n万只医用防护口罩,根据题意列出不等式,解不等式即可得出答案.
18. 21.(本小题满分8分)如图1,在平面直角坐标系中,.
(1)求的面积;
(2)点为坐标轴上一点,若的面积恰好是面积的一半,求点的坐标.
(3)如图2,过点作轴于点,点为延长线上的一动点,连接平分.当点运动时,与度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
【答案】
如图1,过点作轴,重足为
,
,
;
如图1,过点作轴,垂足为
由知,
①当点在轴上时,设
解得:
的坐标为
②当点在轴上时,设
解得:
的坐标为
点的坐标为或
(3)结论:∠OPD=2∠DOE.
理由:如图2,
∵OE平分∠AOP,
∴∠AOE=∠POE=∠1+∠2,
∵OF⊥OE,
∴∠1+∠2+∠3=90°,∠4+∠AOE=90°,
∴∠3=∠4,
∵CD⊥y轴,
∴CD∥AB,
∴∠OPD=∠POB=2∠3,
∵∠1+∠2+∠3=90°,∠2+∠3+∠4=90°,
∴∠1+∠2+∠3=∠2+2∠3,
∴∠1=∠3,
由∠DOE=∠1,∠OPD=∠POB=2∠1
∴∠OPD=2∠DOE.
【解析】
(1)根据三角形的面积公式计算即可.
(2)分两种情形分别构建方程即可解决问题.
(3)根据平行线的性质及证明∠1=∠3即可解决问题.
19. 22.(本小题满分9分)已知,与两个角的角平分线相交于点.
(1)如图1,若,求的度数.
(2)如图2,若,,试写出与之间的数量关系并证明你的结论.
(3)若,,,请直接用含有,的代数式表示出.
【答案】
(1)过F点作FH∥AB,过E点作EG∥AB,如图:
∵
∴FH∥CD,EG∥CD
∴∠ABE+∠BEG=180°,∠GED+∠EDC=180°,∠ABF=∠BFH,∠HFD=∠FDC
∴∠ABE+∠BED+∠EDC=∠ABE+∠BEG+∠GED+∠EDC=360°,∠BFD=∠BFH+∠HFD=∠ABF+∠FDC
∴∠ABE+∠EDC =360°-∠BED
∵与两个角的角平分线相交于点.
∴∠ABF+∠FDC=(∠ABE+∠EDC)=(360°-∠BED)
∵∠BED=80°
∴∠BFD=∠ABF+∠FDC==140°
(2)∠BMD=(360°-∠E),证明:
过M点作MN∥AB,如图:
∵
∴MN∥CD,
∴∠ABM=∠BMN,∠NMD=∠MDC
∴∠BMD=∠BMN+∠NMD=∠ABM+∠MDC
由(1)得:∠ABF+∠FDC=(∠ABE+∠EDC)=(360°-∠E)
∵∠ABM =∠ABF,∠CDM=∠CDF
∴∠BMD=∠ABM+∠MDC=(∠ABF+∠FDC)=(360°-∠E)
(3)由(2)得:∠BMD=∠ABM+∠MDC,由(1)得:∠ABF+∠FDC=(360°-∠BED)
∵,
∴∠BMD=∠ABM+∠MDC=(∠ABF+∠FDC)=(360°-∠BED)=
【解析】
(1)过F点作FH∥AB,过E点作EG∥AB,根据平行线的传递性及平行线的性质可得∠ABE+∠CDE=360°-∠BED,根据平行线的性质可证∠BFD=∠ABF+∠CDF,再根据角平分线的定义求解即可;
(2)过M点作MN∥AB,同一可得∠BMD=∠ABM+∠CDM,由(1)可得∠ABF+∠CDF与∠BED的关系,再根据∠ABM =∠ABF,∠CDM=∠CDF即可求解;
(3)根据(2)中的过程进行推论,总结规律即可.
20. 23.(本小题满分11分)某电脑经销商,今年二,三月份型和型电脑的销售情况,如下表所示:
| 型(台) | 型(台) | 利润(元) |
二月份 | 10 | 20 | 4000 |
三月份 | 20 | 10 | 3500 |
(1)求每台型电脑和型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中型电脑的进货量不超过型电脑的2倍.设购进型电脑台,这100台电脑的销售总利润为元.
①求与的关系式;
②该商店购进型、型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对型电脑出厂价下调元,且限定商店最多购进型电脑70台.若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案.
【答案】
解:(1)设每台型电脑的销售利润为元,每台型电脑的销售利润为元,
则有
解得:
即每台型电脑的销售利润为100元,每台型电脑的销售利润为150元.
(2)①根据题意得,
即
②根据题意得,
解得:,
∵,
∵,
∴随的增大而减小.
∵为正整数,
∴当最小时,取最大值,此时.
即商店购进型电脑34台,型电脑66台,才能使销售总利润最大.
(3)根据题意得,
即.
∵.
①当时,,随的增大而减小,
∴当时,取得最大值.
即商店购进34台型电脑和66台型电脑才能获得最大利润;
②当时,,.
即商店购进型电脑数量满足的整数时,均获得最大利润;
③当时,,随的增大而增大,
∴时,取得最大值.
即商店购进70台型电脑和30台型电脑才能获得最大利润.
【解析】
(1)由题意,设每台型电脑的销售利润为元,每台型电脑的销售利润为元,列出方程组,解方程组即可;
(2)①由题意,根据等量关系,即可列出关系式;
②由题意,根据一次函数的性质,结合x的取值范围,即可求出最大利润;
(3)由题意,先求出关系式,结合一次函数的性质,对m的值进行分类讨论,即可得到答案.
【期末押题复习】2022-2023学年 人教版数学七年级上学期-期末高分精准押题模拟试卷(五): 这是一份【期末押题复习】2022-2023学年 人教版数学七年级上学期-期末高分精准押题模拟试卷(五),共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题02 实数【压轴题专项训练】-2021-2022学年七年级数学下学期期末专项复习(人教版): 这是一份专题02 实数【压轴题专项训练】-2021-2022学年七年级数学下学期期末专项复习(人教版),文件包含专题02实数压轴题专项训练-2021-2022学年七年级数学下学期期末专项复习人教版解析版doc、专题02实数压轴题专项训练-2021-2022学年七年级数学下学期期末专项复习人教版原卷版doc等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
期末检测押题卷(二)-2021-2022学年七年级数学下学期期末专项复习(人教版): 这是一份期末检测押题卷(二)-2021-2022学年七年级数学下学期期末专项复习(人教版),文件包含期末检测押题卷二-2021-2022学年七年级数学下学期期末专项复习人教版解析版doc、期末检测押题卷二-2021-2022学年七年级数学下学期期末专项复习人教版原卷版doc等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












