初中数学人教版七年级下册第五章 相交线与平行线综合与测试课时练习

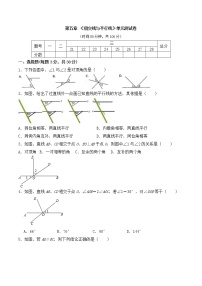
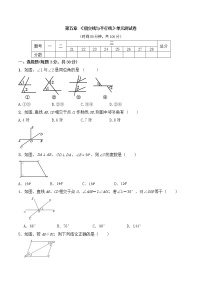
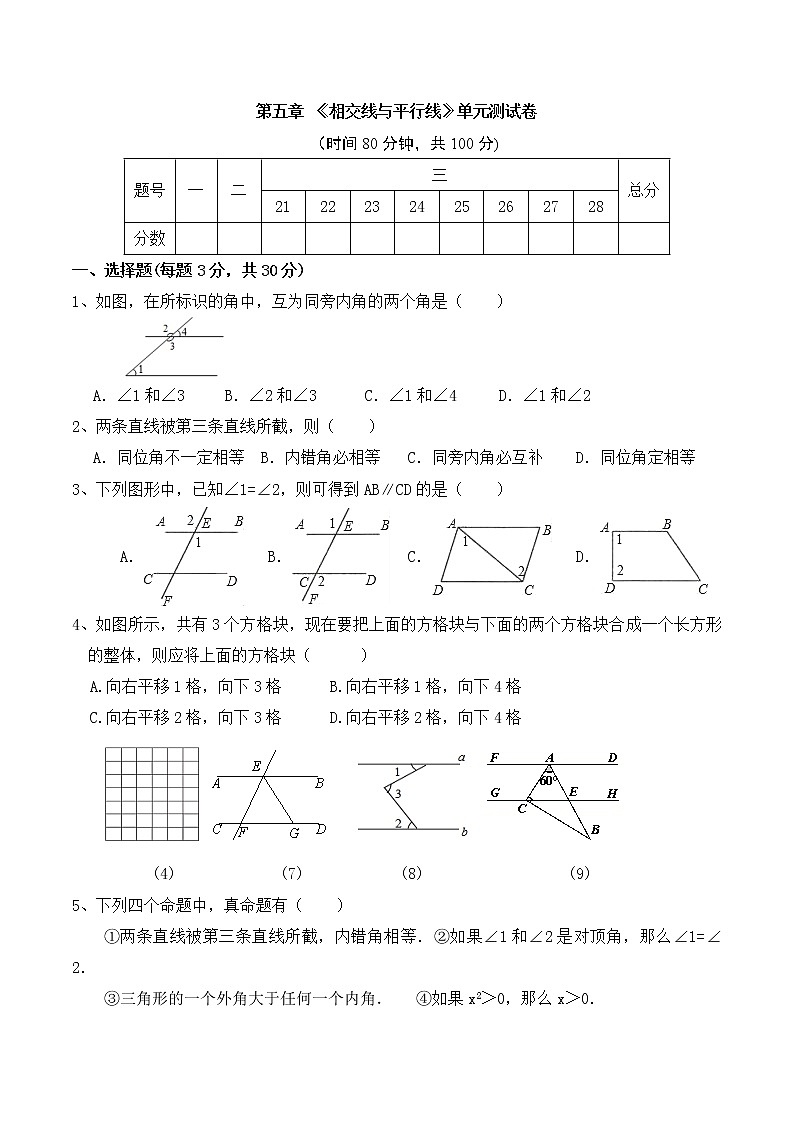
第五章 《相交线与平行线》单元测试卷

  （时间80分钟，共100分)         

一、选择题(每题3分，共30分)

1、如图，在所标识的角中，互为同旁内角的两个角是（　　）

A．∠1和∠3 B．∠2和∠3 C．∠1和∠4 D．∠1和∠2

2、两条直线被第三条直线所截，则（　　）

A．同位角不一定相等  B．内错角必相等 C．同旁内角必互补    D．同位角定相等

3、下列图形中，已知∠1=∠2，则可得到AB∥CD的是（　　）

A． B． C． D．

4、如图所示，共有3个方格块，现在要把上面的方格块与下面的两个方格块合成一个长方形的整体，则应将上面的方格块（      ）

A.向右平移1格，向下3格      B.向右平移1格，向下4格

C.向右平移2格，向下3格      D.向右平移2格，向下4格

(4)                (7)            (8)                  (9)

5、下列四个命题中，真命题有（　　）

①两条直线被第三条直线所截，内错角相等．②如果∠1和∠2是对顶角，那么∠1=∠2．

③三角形的一个外角大于任何一个内角．   ④如果x2＞0，那么x＞0．

A．1个 B．2个   C．3个 D．4个

6．如图，将Rt△ABC沿着点B到C的方向平移到△DEF的位置，AB＝10，DO＝4，平移距离为6，则阴影部分面积为（　　）

A．42 B．96 C．84 D．48

7.在同一平面内有三条直线，若有且只有两条直线平行，则它们（   ）

A.没有交点  只有一个交点  有两个交点  有三个交点

8.两条直线相交所构成的四个角中：①有三个角都相等；   ② 有一对对顶角互补；  ③有一个角是直角；   ④有一对邻补角相等，其中能判定这两条直线垂直的有（   ）

A.1个   B.2个   C.3个   D.4个

9.如图所示，已知AD∥BC，则下列结论：①∠1=∠2；   ②∠2=∠3；   ③ ∠6=∠8；  ④∠5=∠8；⑤∠2=∠4，其中一定正确的是（   ）

A. ②      B.②③⑤   C.①③④     D.②④

10.如图所示，下列判断中错误的是（   ）

A.因为∠A+∠ADC=180°，所以AB∥CD  

B.因为AB∥CD，所以∠ABC+∠C=180°

C.因为∠1=∠2，所以AD∥BC      

D.因为AD∥BC，所以∠3=∠4

二、填空题(每题3分，共24分)

11．如图，直线a，b被直线c所截，若a∥b，∠1=40°，∠2=70°，则∠3=　　度．

第11题图                            第12题图  

12．如图，有一块长为32 m、宽为24 m的长方形草坪，其中有两条直道将草坪分为四块，则分成的四块草坪的总面积是________m2.

13．如图，AB∥CD，∠BAE=120°，∠DCE=30°，则∠AEC=　　度．

14．如图，将边长为12的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，当两个三角形重叠部分的面积为32时，它移动的距离AA′等于　　．

15.如图，，要使，应添加的一个条件是__填一个即可

    （第15题图）   （第18题图）

16.已知，，则的度数为____________．

17.有下列说法：两条直线的位置关系只有相交、平行两种；过直线外一点可以有多条不同直线与已知直线平行；若以，，则；在同一平面内两条不平行的线段必相交；与已知直线平行的直线有且只有一条．其中说法正确的为          填序号．

18.如图，，，，，，则______度．      

三.解答题(共46分)

19.（6分）已知：如图，∠B=∠ADE，∠EDC=∠GFB，GF⊥AB.求证：CD⊥AB.

20.(8分）如图，已知∠1+∠2=180，∠3=∠B,试判断∠AED与∠C的大小关系，并对结论    进行说理。

21．（8分）如图，AD是∠CAB的平分线，DE∥AB，DF∥AC，EF交AD于点O，请问：

（1）DO是∠EDF的平分线吗？如果是，请给予证明，如果不是，请说明理由．

（2）若将“DO是∠EDF的平分线”与“AD是∠CAB的平分线”，“DE∥AB”，“DF∥AC”中的任一条件交换，所得命题正确吗？若正确，请选择一个证明．

22.（8分）如图，已知∠1+∠2＝180°，∠3＝∠B．

（1）试判断DE与BC的位置关系，并说明理由．

（2）若DE平分∠ADC，∠2＝3∠B，求∠1的度数．

23．（8分）图1，点E在直线AB上，点F在直线CD上，EG⊥FG．

(1)若∠BEG＋∠DFG＝90°，请判断AB与CD的位置关系，并说明理由；

(2)如图2，在(1)的结论下，当EG⊥FG保持不变，EG上有一点M，使∠MFG＝2∠DFG，则∠BEG与∠MFG存在怎样的数量关系？并说明理由；

(3)如图2，若移动点M，使∠MFG＝n∠DFG，请直接写出∠BEG与∠MFG的数量关系．

24．（8分）如图，若AB∥CD，在下列三种情况下探究∠APC与∠PAB，∠PCD的数量关系．

（1）图①中，∠APC+∠PAB+∠PCD=　　；

（2）图②中，　　；

（3）图③中，写出∠APC与∠PAB，∠PCD的三者数量关系，并说明理由．

参考答案

一、选择题:

二、填空题:

11.110　度        12.660

13.90　度.         14.4或8；

15、

16、或．

17、

18、134

三.解答题:

19．∵∠B=∠ADE

∴DE∥BC

∴∠EDC=∠DCB

又∵∠EDC=∠GFB

∴∠GFB=∠DCB

∴GF∥CD

∵GF ⊥AB

∴∠BFG=90°

∴∠BDC=90°

∴CD ⊥AB

20. ∠AED=∠C

∵∠1+∠2=180°，∠1+∠4=180°

∴∠2=∠4

∴EF∥AB

∠3=∠ADE

又∵∠3=∠B

∴∠B=∠ADE

∴DE∥BC

∴∠AED=∠C

21．

【解答】解：（1）是．

理由：∵DE∥AB，DF∥AC，

∴∠EDA＝∠DAB，∠EAD＝∠ADF，

∵AD是∠CAB的平分线

∴∠EAD＝∠DAB，

∴∠EDA＝∠ADF，

∴DO是∠EDF的平分线．

（2）正确．

选择命题：若DO是∠EDF的平分线，DE∥AB，DF∥AC，则AD是∠CAB的平分线．

理由：∵DE∥AB，DF∥AC，

∴∠EDA＝∠DAB，∠EAD＝∠ADF，

∵DO是∠EDF的平分线

∴∠EDA＝∠ADF，

∴∠EAD＝∠DAB，

∴AD是∠CAB的平分线．

22.解：（1）DE∥BC，理由如下：

∵∠1+∠4＝180°，∠1+∠2＝180°，

∴∠2＝∠4，

∴AB∥EF，

∴∠3＝∠5，

∵∠3＝∠B，

∴∠5＝∠B，

∴DE∥BC，

（2）∵DE平分∠ADC，

∴∠5＝∠6，

∵DE∥BC，

∴∠5＝∠B，

∵∠2＝3∠B，

∴∠2+∠5+∠6＝3∠B+∠B+∠B＝180°，

∴∠B＝36°，

∴∠2＝108°，

∵∠1+∠2＝180°，

∴∠1＝72°．

23．解：(1)AB∥CD．理由如下：如图1，延长EG交CD于点H．∴∠HGF＝∠EGF＝90°，∴∠GHF＋∠GFH＝90°．∵∠BEG＋∠DFG＝90°，∴∠BEG＝∠GHF，∴AB∥CD．

(2)∠BEG＋∠MFG＝90°．理由如下：如图2，延长EG交CD于点H．∵AB∥CD，∴∠BEG＝∠GHF．∵EG⊥FG，∴∠GHF＋∠GFH＝90°．∵∠MFG＝2∠DFG，∴∠BEG＋∠MFG＝90°．

(3)∠BEG＋∠MFG＝90°．理由如下：∵AB∥CD，∴∠BEG＝∠GHF．∵EG⊥FG，∴∠GHF＋∠GFH＝90°．∵∠MFG＝n∠DFG，∴∠BEG＋∠MFG＝90°．

24．解：（1）过P作PE∥AB，

∵AB∥CD，

∴PE∥CD，

∴∠A+∠APE=180°，∠EPC+∠C=180°，

∴∠APC+∠PAB+∠PCD=∠A+∠APE+∠EPC+∠C=360°；

（2）过P作PE∥AB，

∵AB∥CD，

∴PE∥CD，

∴∠A=∠APE，∠EPC=∠C，

∴∠APC=∠APE+∠EPC=∠PAB+∠PCD；

（3）∠APC=∠PCD﹣∠PAB，

理由为：过P作PE∥AB，

∵AB∥CD，

∴PE∥CD，

∴∠PAB+∠APE=180°，∠EPC+∠PCD=180°，

即∠APE=180°﹣∠PAB，∠EPC=180°﹣∠PCD，

∴∠APC=∠APE﹣∠EPC=∠PCD﹣∠PAB．

故答案为：（1）360°；（2）∠APC=∠PAB+∠PCD