02相交线，垂线（提高）知识讲解练习题

相交线，垂线（提高）知识讲解

【学习目标】

1.了解两直线相交所成的角的位置和大小关系，理解邻补角和对顶角概念，掌握对顶角的性质；

2.理解垂直作为两条直线相交的特殊情形，掌握垂直的定义及性质；

3.理解点到直线的距离的概念，并会度量点到直线的距离；

4.能依据对顶角、邻补角及垂直的概念与性质，进行简单的计算.

【要点梳理】

知识点一、邻补角与对顶角

1．邻补角：如果两个角有一条公共边，并且它们的另一边互为反向延长线，那么具有这种关系的两个角叫做互为邻补角．

要点诠释：

(1)邻补角的定义既包含了位置关系，又包含了数量关系：“邻”指的是位置相邻，“补”指的是两个角的和为180°．

(2)邻补角是成对出现的，而且是“互为”邻补角．

(3)互为邻补角的两个角一定互补，但互补的两个角不一定互为邻补角．

(4)邻补角满足的条件：①有公共顶点；②有一条公共边；另一边互为反向延长线.

2. 对顶角及性质：

 （1）定义：由两条直线相交构成的四个角中，有公共顶点没有公共边(相对)的两个角，互为对顶角．

 （2）性质：对顶角相等．

要点诠释：

(1)由定义可知只有两条直线相交时，才能产生对顶角．

(2)对顶角满足的条件：①相等的两个角；②有公共顶点且一角的两边是另一角两边的反向延长线.

3. 邻补角与对顶角对比：        

知识点二、垂线

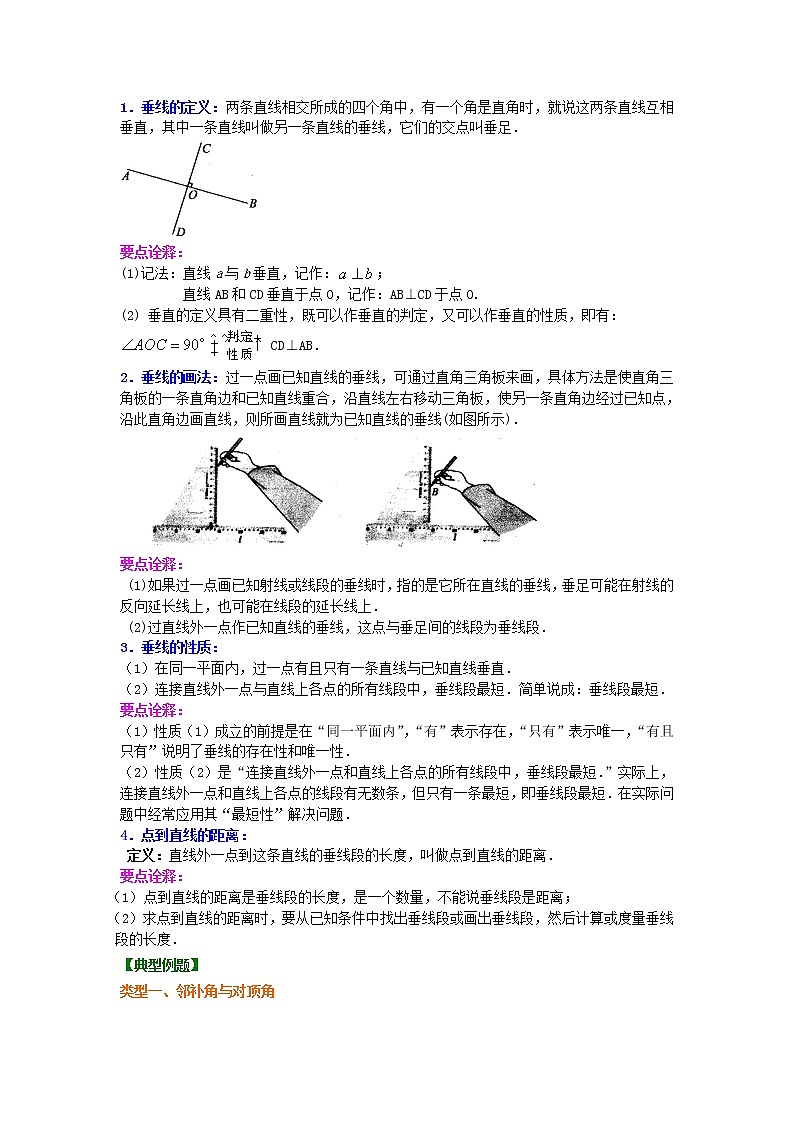
1．垂线的定义：两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫垂足．

要点诠释：

(1)记法：直线a与b垂直，记作：；

         直线AB和CD垂直于点O，记作：AB⊥CD于点O.

(2) 垂直的定义具有二重性，既可以作垂直的判定，又可以作垂直的性质，即有：

CD⊥AB．

2．垂线的画法：过一点画已知直线的垂线，可通过直角三角板来画，具体方法是使直角三角板的一条直角边和已知直线重合，沿直线左右移动三角板，使另一条直角边经过已知点，沿此直角边画直线，则所画直线就为已知直线的垂线(如图所示)．

要点诠释：

 (1)如果过一点画已知射线或线段的垂线时，指的是它所在直线的垂线，垂足可能在射线的反向延长线上，也可能在线段的延长线上．

(2)过直线外一点作已知直线的垂线，这点与垂足间的线段为垂线段．

3．垂线的性质：

（1）在同一平面内，过一点有且只有一条直线与已知直线垂直．

（2）连接直线外一点与直线上各点的所有线段中，垂线段最短．简单说成：垂线段最短．

要点诠释：

（1）性质（1）成立的前提是在“同一平面内”，“有”表示存在，“只有”表示唯一，“有且只有”说明了垂线的存在性和唯一性．

（2）性质（2）是“连接直线外一点和直线上各点的所有线段中，垂线段最短．”实际上，连接直线外一点和直线上各点的线段有无数条，但只有一条最短，即垂线段最短．在实际问题中经常应用其“最短性”解决问题．

4．点到直线的距离：

定义：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．

要点诠释：

（1） 点到直线的距离是垂线段的长度，是一个数量，不能说垂线段是距离；

（2）求点到直线的距离时，要从已知条件中找出垂线段或画出垂线段，然后计算或度量垂线段的长度．

【典型例题】

类型一、邻补角与对顶角

1．如图所示，AB和CD相交于点O，OM平分∠AOC，ON平分∠BOD，试说明OM和ON成一条直线。

【答案与解析】

解：∵ OM平分∠AOC，ON平分∠BOD（已知），

∴ ∠AOC=2∠AOM，∠BOD=2∠BON（角平分线定义）。

∵∠AOC=∠BOD（对顶角相等），∴∠AOM=∠BON（等量代换）。

∵∠AON+∠BON=180°（邻补角定义），∴∠MON=∠AON+∠AOM=180°（等量代换），

∴ OM和ON共线。

【总结升华】要得出OM和ON成一条直线，就要说明∠MON是平角，从图中可以看出∠AON是∠MON和平角∠AOB的公共部分，所以只要证明它们的非公共部分相等，即∠AOM和∠BON相等，本题得证。

2.如图所示，已知直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠2:∠1＝4:l，求．

【答案与解析】

解：设∠1＝x，则∠2＝4x．

∵  OE平分∠BOD，∴  ∠BOD＝2∠1＝2x．

∵  ∠2+∠BOD＝180°，即4x+2x＝180°，∴  x＝30°．

∵  ∠DOE+∠COE＝180°，∴  ∠COE＝150°．

又∵  OF平分∠COE，∴  ∠COF＝∠COE＝75°．

∵  ∠AOC＝∠BOD＝60°，∴  ∠AOF＝∠AOC+∠COF＝60°+75°＝135°．

【总结升华】涉及有比值的题设条件，如a:b＝m:n，在解题时设，，这是常用的用方程思想解题的方法．

举一反三：

【变式】已知α的补角是一个锐角，有3人在计算时的答案分别是32°、87°、58°，其中只有一个答案是正确的，求的度数．

【答案】

解法1：∵  α的补角是一个锐角，

∴  α是一个钝角，即90°＜α＜180°，

∴  ．

由已知三人计算出的答案分别为32°、87°、58°，

可知．

∴  ．

解法2：由题意可知是一个钝角，即．

如果，那么，不满足；

如果，那么，不满足；

如果，那么，满足，

所以此人计算的答案正确．所以．

【总结升华】在处理数学问题中的误选答案问题时，常采用验算法，如本题的解法2：先利用假设求出相应的α的度数，再验证是否正确．

3.（1）如图（1），已知直线a、b相交于点 O，则（1）图中共有几对对顶角?几对邻补角？

（2）如图（2），已知直线a、b、c、d是经过点O的四条直线，则图（2）中共有几对对顶角（不含平角）?几对邻补角？

【答案与解析】

解：（1）2对对顶角，4对邻补角。

（2）将图（2）拆分为下图：

通过观察图形．不难发现a、b、c、d四条直线两两相交，最多有6个交点，而由（1）知：每个交点处有两对对顶角，有四对邻补角，

对顶角的对数：（对）；邻补角的对数:(对)

答：图中共有12对对顶角，24对邻补角

【总结升华】本例分析问题的方法是通过直线的移动，将直线相交于一点转化为直线两两相交．这样移动，可将抽象的问题直观化．因为n条直线两两相交，最多有个交点．每个交点处有两组对顶角，故n条直线相交于一点共有n(n-1)对对顶角，2n(n-1)对邻补角。

举一反三：

【变式】（2015•青岛模拟）如图，直线AB与CD相交所成的四个角中，∠1的邻补角是　    　，∠1的对顶角是　  　．

【答案】∠ 2和∠ 4；∠ 3.

由图形可知，∠1的对顶角是∠3，∠1的邻补角是∠2和∠4．

类型二、垂线

4．下列语句：

①两条直线相交，若其中一个交角是直角，那么这两条直线垂直。

②一条直线的垂线有无数条。

③空间内过一点有且只有一条直线与已知直线垂直；

④两条直线相交成四个角，如果有两个角相等，那么这两条直线垂直。

其中正确的是＿＿＿＿＿＿＿＿＿＿。

【答案】①②

【解析】解此题必须严格按照垂线的定义“两条直线相交成直角”及垂线的性质“过平面内任意一点，即过直线上或直线外任意一点，有且仅有一条直线与已知直线垂直”来作判断。

①正确；②正确，过任意一点都可以作；对于③只有在“同一平面内”才成立，因为空间内，当这点在直线上时，过这点并非只有一条直线与已知直线垂直，故③错误；④错误，必须是两个邻角相等，如下图：

【总结升华】应用垂线的定义及垂线的性质时要把握其中的本质要求：

①关于垂线的定义：要判断两条直线是否垂直，只需看它们相交所成的四个角中，是否有一个角是直角，两条线段垂直，是指这两条线段所在的直线垂直；

②关于垂线的性质：平面内，过任意一点有且仅有一条直线与已知直线垂直，这条性质说明了已知直线的垂线的“存在性”和“唯一性”，尤其值得注意的是性质中的“任意一点”可能在这条已知直线上，也可能在这条已知直线外。

举一反三：

【变式】在铁路旁有一城镇，现打算从城镇修一条和铁路垂直的道路，这种方案是唯一的，是因为(    )

A．经过两点有且只有一条直线

B．两点之问的所有连线中，线段最短

C．在同一平面内，两直线同时垂直同一条直线，则这两直线也互相垂直．

D．在同一平面内，过一点有且只有一条直线与已知直线垂直

【答案】D   提示：注意区分直线性质与垂线性质

 5.（2016春•达州校级期中）如图所示，OA⊥OB，OC⊥OE，OD为∠BOC的平分线，∠BOE=20°，求∠DOE的度数．

【思路点拨】首先根据垂直定义以及角平分线的定义得出∠BOD的度数，进而得出∠DOE的度数．

【答案与解析】

解：∵OC⊥OE，

∴∠COE=90°，

∵∠BOE=20°，

∴∠COB=90°+20°=110°，

∵OD为∠BOC的平分线，

∴∠BOD=55°，

∴∠DOE=55°﹣20°=35°．

【总结升华】此题主要考查了角平分线的定义以及垂直定义，正确求出∠COB的度数是解题关键．

举一反三：

【变式】如图，若OM平分∠AOB，且OM ⊥ON，求证：ON平分∠BOC.

【答案】

解：如图，

∵OM平分∠AOB     ∴∠1=∠2

又∵OM ⊥ON     ∴∠3=90°－∠2

由图可得：∠4=180°－2∠2－∠3=180°－2∠2 －（90°－∠2）=90°－∠2

∴∠3=∠4

∴ ON平分∠BOC

6.如图所示，一辆汽车在直线形公路AB上由A向B行驶，M、N分别是位于公路两侧的村庄．

    (1)设汽车行驶到公路AB上点P位置时，距离村庄M最近；行驶到点Q位置时，距离村庄N最近，请在图中的公路AB上分别画出点P和点Q的位置(保留作图痕迹)．

    (2)当汽车从A出发向B行驶时，在公路AB的哪一段路上距离M、N两村庄都越来越近?在哪一段路上距离村庄N越来越近，而离村庄M越来越远?(分别用文字表述你的结论，不必说明)

【答案与解析】

解：(1)过点M作MP⊥AB，垂足为P，过点N作NQ⊥AB，垂足为Q，点P、Q就是要画的两点，如图所示．

(2)当汽车从A向B行驶时，在AP这段路上，离两个村庄越来越近；在PQ这段路上，离村庄M越来越远，离村庄N越来越近．

【总结升华】利用垂线段最短解决实际问题是常用的一种方法．

举一反三：

【变式1】如图所示，过A点作AD⊥BC，垂足为D点．

【答案】

解：如图所示

【变式2】点P为直线外一点：点A、B、C为直线上三点，PA＝4 cm，PB＝5 cm，PC＝2 cm，则点P到直线的距离是  (    )

A．2 cm    B．4 cm    C．5 cm    D．不超过2 cm

【答案】D.