37角（提高）知识讲解练习题

角（提高）

【学习目标】

1．掌握角的概念及角的几种表示方法，并能进行角度的互换；

2. 借助三角尺画一些特殊角，掌握角大小的比较方法；

3. 掌握角的和、差、倍、分关系，并会进行有关计算；

4. 掌握互为余角和互为补角的概念及性质，会用余角、补角及性质进行有关计算；

5．了解方位角的概念，并会用方位角解决简单的实际问题．

【要点梳理】

【要点梳理】

知识点一、角的概念

1． 角的定义：

（1）定义一：有公共端点的两条射线组成的图形叫做角，这个公共端点是角的顶点，这两条射线是角的两条边．如图1所示，角的顶点是点O，边是射线OA、OB．

（2）定义二：一条射线绕着它的端点旋转而形成的图形，射线旋转时经过的平面部分是角的内部．如图2所示，射线OA绕它的端点O旋转到OB的位置时，形成的图形叫做角，起始位置OA是角的始边，终止位置OB是角的终边．

要点诠释：

（1）两条射线有公共端点，即角的顶点；角的边是射线；角的大小与角的两边的长短无关．

（2）平角与周角：如图1所示射线OA绕点O旋转，当终止位置OB和起始位置OA成一条直线时，所形成的角叫做平角，如图2所示继续旋转，OB和OA重合时，所形成的角叫做周角．

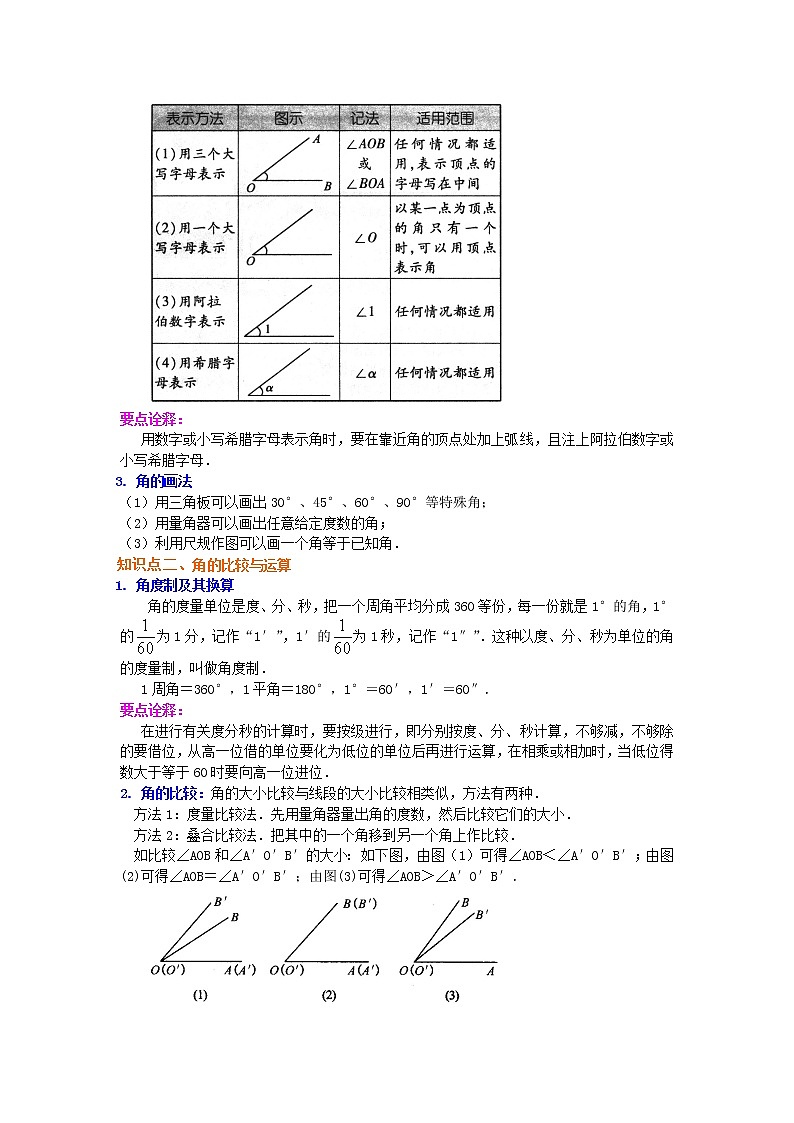
2. 角的表示法：角的几何符号用“∠”表示，角的表示法通常有以下四种：

要点诠释：

用数字或小写希腊字母表示角时，要在靠近角的顶点处加上弧线，且注上阿拉伯数字或小写希腊字母．

3. 角的画法

（1）用三角板可以画出30°、45°、60°、90°等特殊角；

（2）用量角器可以画出任意给定度数的角；

（3）利用尺规作图可以画一个角等于已知角．

知识点二、角的比较与运算

1. 角度制及其换算

    角的度量单位是度、分、秒，把一个周角平均分成360等份，每一份就是1°的角，1°的为1分，记作“1′”，1′的为1秒，记作“1″”．这种以度、分、秒为单位的角的度量制，叫做角度制．

   1周角＝360°，1平角＝180°，1°＝60′，1′＝60″．

要点诠释：

在进行有关度分秒的计算时，要按级进行，即分别按度、分、秒计算，不够减，不够除的要借位，从高一位借的单位要化为低位的单位后再进行运算，在相乘或相加时，当低位得数大于等于60时要向高一位进位．

2. 角的比较：角的大小比较与线段的大小比较相类似，方法有两种．

方法1：度量比较法．先用量角器量出角的度数，然后比较它们的大小．

方法2：叠合比较法．把其中的一个角移到另一个角上作比较．

如比较∠AOB和∠A′O′B′的大小： 如下图，由图（1）可得∠AOB＜∠A′O′B′；由图(2)可得∠AOB＝∠A′O′B′；由图(3)可得∠AOB＞∠A′O′B′．

3. 角的和、差关系

如图所示，∠AOB是∠1与∠2的和，记作：∠AOB＝∠1+∠2；∠1是∠AOB与∠2的差，记作：∠1＝∠AOB-∠2．

要点诠释：

(1)用量角器量角和画角的一般步骤：①对中(角的顶点与量角器的中心对齐)；②重合(一边与刻度尺上的零度线重合)；③读数(读出另一边所在线的度数)．

 (2) 利用三角板除了可以做出30°、45°、60°、90°外，根据角的和、差关系，还可以画出15°，75°，105°，120°，135°，150°，165°的角．

4. 角平分线

从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线．如图所示，OC是∠AOB的角平分线，∠AOB＝2∠AOC＝2∠BOC，

∠AOC＝∠BOC =∠AOB．

要点诠释：由角平分线的概念产生的合情推理其思维框架与线段中点的思维框架一样．

知识点三、余角和补角

1. 定义：一般地，如果两个角的和等于90°(直角)，就说这两个角互为余角，即其中一个角是另一个角的余角．

    类似地，如果两个角的和等于180°(平角)，就说这两个角互为补角，即其中一个角是另一个角的补角．

2．性质：（1）同角（等角）的余角相等．（2）同角（等角）的补角相等．

要点诠释：

(1)互余互补指的是两个角的数量关系，互余、互补的两个角只与它们的和有关，而与它们的位置无关．

 (2)一般地，锐角α的余角可以表示为(90°-α)，一个角α的补角可以表示为(180°-α) ．显然一个锐角的补角比它的余角大90°．

知识点四、方位角

在航行和测绘等工作中，经常要用到表示方向的角．例如，图中射线OA的方向是北偏东60°；射线OB的方向是南偏西30°．这里的“北偏东60°”和“南偏西30°”表示方向的角，就叫做方位角．

要点诠释：

（1）正东，正西，正南，正北4个方向不需要用角度来表示；

（2）方位角必须以正北和正南方向作为“基准”，“北偏东60°”一般不说成“东偏北30°”；

（3）在同一问题中观察点可能不止一个，在不同的观测点都要画出表示方向的“十字线”，确定其观察点的正东、正西、正南、正北的方向；

（4）图中的点O是观测点，所有方向线(射线)都必须以O为端点．

知识点五、钟表上有关夹角问题

钟表中共有12个大格，把周角12等分、每个大格对应30°的角，分针1分钟转6°，时针每小时转30°，时针1分钟转0.5°，利用这些关系，可帮助我们解决钟表中角度的计算问题．

【典型例题】

类型一、角的比较与运算

1. 利用一副三角板上的角，能画出多少个小于180°的角，试一一画出来．

【思路点拨】首先发现一副三角板上有30°，45°，60°，90°这样4个不相等的角，利用这些角进行一次和差，可得小于180°的所有角．

【答案与解析】

解：除了可以画30°，45°，60°，90°外，还可画15°，75°，105°，120°，135°，150°，165°的七个度数的角，画法如图所示．

【总结升华】利用一副三角板共可以画出11个度数的角，分别是：30°，45°，60°，90°，15°，75°，105°，120°，135°，150°，165°．

2. 计算下列各题：

    (1)152°49′12″+20.18°；    (2)82°-36°42′15″；

    (3)35°36′47″×9；          (4)41°37′÷3．

 【答案与解析】

  解：(1)解法一：∵  20.18°＝20°10′48″

    即：152°49′12″+20.18°＝173°．

    解法二：∵  152°49′12″＝152.82°，

    ∴  152.82°+20.18°＝173°．

    即：152°49′12″+20.18°＝173°．

    (2)将82°化为81°59′60″，则

∴  82°-36°42′15″＝45°17′45″．

    423″＝7′3″，   324′+7′＝5°31′，

    ∴  35°36′47″×9＝320°31′3″．

∴ 41°37′÷3=13°52′20″．

【总结升华】在角度的和、差运算中应先统一单位，都化成度或分、秒表示，然后进行计算；在进行乘法运算时，往往先把度、分、秒分别乘以倍数，将结果满60″进1′，满60′进1°；对于除法运算则是从度开始除，将余数化为分和以前的分数相加再除，将余数再化成秒和以前的秒数相加再除，若除不尽往往四舍五入．

举一反三：

【变式】计算：

    (1)23°45′36″+66°14′24″；(2)180°-98°24′30″；

    (3)15°50′42″×3；          (4)88°14′48″÷4．

【答案】(1)23°45′36″+66°14′24″＝90°；

(2)180°-98°24′30″＝81°35′30″；

(3)15°50′42″×3＝47°32′6″；

(4)88°14′48″÷4＝22°3′42″．

3.（2016春•龙口市期中）如图，∠AOB=90°，∠AOC=30°，且OM平分∠BOC，ON平分∠AOC，

（1）求∠MON的度数；

（2）若∠AOB=α其他条件不变，求∠MON的度数；

（3）若∠AOC=β（β为锐角）其他条件不变，求∠MON的度数；

（4）从上面结果中看出有什么规律？

【思路点拨】（1）要求∠MON，即求∠COM﹣∠CON，再根据角平分线的概念分别进行计算即可求得；（2）和（3）均根据（1）的计算方法进行推导即可．（4）根据（2）和（3）中的结论进行总结．

【答案与解析】

解：（1）∵∠AOB=90°，∠AOC=30°，

∴∠BOC=120°

∵OM平分∠BOC，ON平分∠AOC

∴∠COM=60°，∠CON=15°

∴∠MON=∠COM﹣∠CON=45°．

（2）∵∠AOB=α，∠AOC=30°，

∴∠BOC=α+30°

∵OM平分∠BOC，ON平分∠AOC

∴∠COM=+15°，∠CON=15°

∴∠MON=∠COM﹣∠CON=．

（3）∵∠AOB=90°，∠AOC=β，

∴∠BOC=90°+β

∵OM平分∠BOC，ON平分∠AOC

∴∠COM=45°+，∠CON=．

∴∠MON=∠COM﹣∠CON=45°．

（4）从上面的结果中，发现：

∠MON的大小只和∠AOB得大小有关，与∠A0C的大小无关．

【总结升华】能够结合图形表示角之间的和差关系，根据角平分线的概念运用几何式子表示角之间的倍分关系．

举一反三：

【变式】如图，∠AOB的平分线OM,ON为∠MOA内的一条射线，OG为∠AOB外的一条射线。某同学经过认真分析，得到一个关系式是∠MON=（∠BON－∠AON），你认为这个同学得到的关系式正确吗？若正确，请把得到这个结论的过程写出来。

【答案】

解：正确，理由如下：

∵∠AOB的平分线OM，

∴∠AOM=∠MOB

又∵∠MON=∠AOM－∠AON=∠MOB－∠AON=(∠BON－∠MON) －∠AON

即有∠MON=∠BON－∠MON －∠AON

∴ 2∠MON=∠BON－∠AON

∴∠MON=（∠BON－∠AON）

类型二、余角与补角

4.已知点O是直线AB上的一点，∠COE＝90°，OF是∠AOE的平分线．

    (1)当点C、E、F在直线AB的同侧(如图①所示)时．试说明∠BOE＝2∠COF；

    (2)当点C与点E、F在直线AB的两旁(如图②所示)时(1)中的结论是否仍然成立?请给出你的结论并说明理由；

    (3)将如图②中的射线OF绕点O顺时针旋转m°(0＜m＜180)，得到射线OD，设∠AOC＝n°，若∠BOD＝，则∠DOE的度数是多少?(用含n的式子表示)

【思路点拨】由于本题中涉及角的数量关系，故可以选择代数的方法来说明理由．

【答案与解析】

解：(1)如图①，设∠COF＝α，  则∠EOF＝90°-α

    因为OF是∠AOE的平分线

    所以∠AOF＝90°-α

    所以∠AOC＝(90°-α)-α＝90°-2α

    ∠BOE＝180°-∠COE-∠AOC

         ＝180°-90°-(90°-2α)＝2α

    即∠BOE＝2∠COF

    (2)成立．如图2

    设∠AOC＝β，则，

    所以

    ∠BOE＝180°-∠AOE＝180°-(90°-β)＝90°+β

    所以∠BOE＝2∠COF

    (3)因为∠DOE＝180°-∠AOE-∠BOD

                 .

    故的度数是.

【总结升华】根据角平分线，互余及互补的定义，进行有关角的计算．有一定的综合性和代表性，主要培养分析问题和解决问题的能力．

举一反三：

【变式1】如图，已知O是直线AC上一点，OD平分AOB，OE在BOC内，且BOE＝EOC，DOE＝70°，求EOC的度数.

【答案】

解：设∠EOC=°，则BOE＝EOC＝°，根据题意可得：

.

解得：.

∴ EOC＝2BOE＝80°.

【变式2】（2015•百色）一个角的余角是这个角的补角的，则这个角的度数是（　　）

　A．30° B． 45° C． 60° D． 70°

【答案】 B．

解：设这个角的度数为x，则它的余角为90°﹣x，补角为180°﹣x，

依题意得：90°﹣x=（180°﹣x），

解得x=45°．

类型三、方位角

5. （2015•浦东新区三模）已知小岛A位于基地O的东南方向，货船B位于基地O的北偏东50°方向，那么∠AOB的度数等于　   　．

【答案】85°．

【解析】

解：如图：∵∠2=50°，

∴∠3=40°，

∵∠1=45°，

∴∠AOB=∠1+∠3=45°+40°=85°，

故答案为：85°．

【总结升华】本题主要考查了方位角的概念，根据方位角的概念，画图正确表示出A，B的方位，注意东南方向是45度是解答此题的关键．

类型四、钟表上有关夹角问题

6. 在7时到7时10分之间的什么时刻，时针与分针成一条直线?

【答案与解析】  

 解：设7时x分钟，时针与分针成一条直线，由题意得：

    ，．

    答：7时分钟时针与分针成一条直线．

【总结升华】时钟上的分针与时针绕着中心顺时针均匀转动，在不同时刻，两针之间形成一定的角度．如果把单位时间分针和时针转过的度数当作它们的速度则：

①     分针的速度为＝6°/分；②时针的速度为＝0.5°/分．

故分针速度是时针速度的12倍．

举一反三：

【变式】某人下午6点多外出购物，表上的时针和分针的夹角恰为110°，下午近7点回家时，发现表上的时针和分针的夹角又是110°，试算出此人外出用了多长时间?

【答案】

解法一：设此人外出用了x分钟，则分针转了6x度，时针转了0.5x度．根据题意得：

6x-0.5x＝110×2，解之得x＝40．

答：此人外出购物用了40分钟的时间．

解法二：设时针从某人外出到回家走了x°，则分针走了（110＋110+x）°，则：
　　 110＋x＋110＝12x，
　　 解得x＝20．
　　 又∵时针每分钟转0.5°，
　　 ∴此人外出用的时间为：20÷0.5＝40（分钟）．
答：此人外出购物用了40分钟的时间．