2021学年第二章 直角三角形的边角关系综合与测试习题ppt课件

这是一份2021学年第二章 直角三角形的边角关系综合与测试习题ppt课件，共34页。PPT课件主要包含了答案呈现，习题链接等内容，欢迎下载使用。

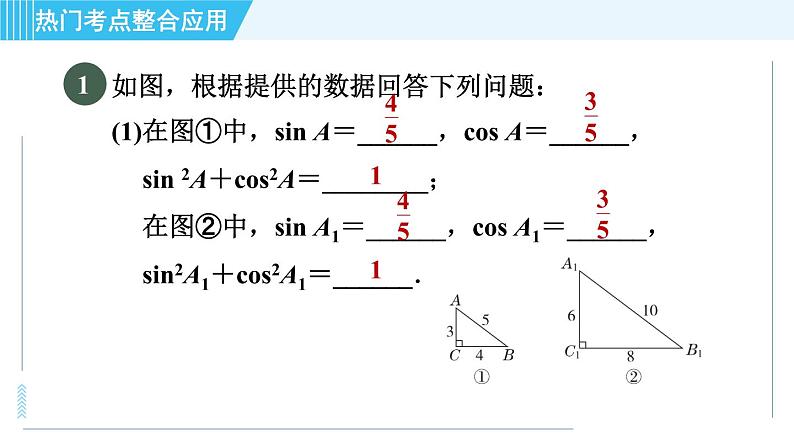
如图，根据提供的数据回答下列问题：(1)在图①中，sin A＝______，cs A＝______，sin 2A＋cs2A＝________；在图②中，sin A1＝______，cs A1＝______，sin2A1＋cs2A1＝______．
通过以上两个特殊例子，你发现了什么规律？用一个一般式表示出你的发现并加以证明．
(2)利用你发现的规律求解以下题目：已知β是锐角，且满足sin β＝3cs β，求sin β，cs β的值．
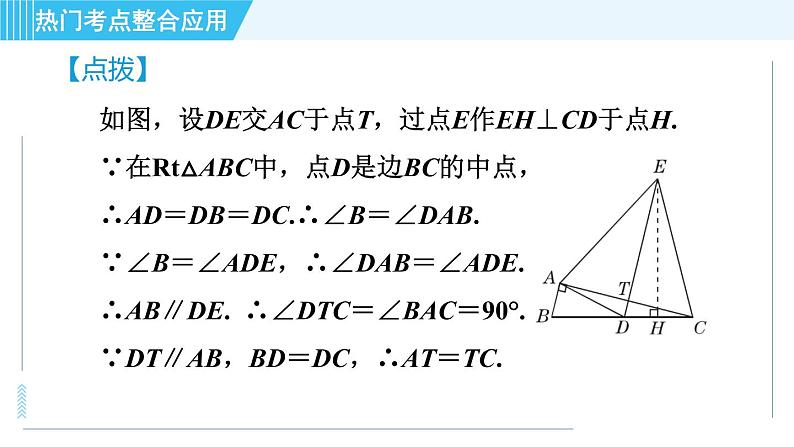
如图，设DE交AC于点T，过点E作EH⊥CD于点H.∵在Rt△ABC中，点D是边BC的中点，∴AD＝DB＝DC.∴∠B＝∠DAB.∵∠B＝∠ADE，∴∠DAB＝∠ADE.∴AB∥DE. ∴∠DTC＝∠BAC＝90°.∵DT∥AB，BD＝DC，∴AT＝TC.
计算下列各式的值. (1)2sin 30°＋3cs 60°－4tan 45°；(2)cs230°·sin 45°＋sin230°·cs 45°；
【2021·济宁期末】如图，在Rt△AOB中，已知AO＝6 cm，BO＝8 cm.点P从点B开始沿BA边向终点A以1 cm/s的速度移动；点Q从点A开始沿AO边向终点O以1 cm/s的速度移动．若P，Q同时出发，运动时间为t s.(1)当t为何值时，以A，P，Q为顶点的三角形与△AOB相似？
(2)当t为何值时，△APQ的面积为8 cm2?
【2021·连云港】我市的前三岛是众多海钓人的梦想之地，小明的爸爸周末去前三岛钓鱼，将鱼竿AB如图①摆放，已知AB＝4.8 m，鱼竿尾端A离岸边0.4 m，即AD＝0.4 m，海面与地面AD平行且相距1.2 m，即DH＝1.2 m.
(1)如图①，在无鱼上钩时，海面上方的鱼线BC与海面HC的夹角∠BCH＝37°，海面下方的鱼线CO与海面HC垂直，鱼竿AB与地面AD的夹角∠BAD＝22°，求点O到岸边DH的距离；
通过学习锐角三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值是一一对应的，因此两条边长的比值与角的大小之间可以相互转化．类似地，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做底角的邻对(记作can)．
解：方法一：如图①，过点B作BE∥AD交DC于点E，过点E作EF∥AB交AD于点F，易得BE⊥BA，EF⊥AD.∴四边形ABEF是矩形．∴EF＝AB，AF＝BE.∵∠ABC＝120°，∴∠CBE＝120°－90°＝30°，∠D＝360°－90°－90°－120°＝60°.