

2022届新教材北师大版平面向量单元测试含答案19
展开
2022届新教材北师大版 平面向量 单元测试
一、选择题
1、在△ABC中,=(2,3),=(1,k),若△ABC为直角三角形,则k的值为 ( )
A. - B. C. -或 D. -、或
2、在矩形中, , , ,点在边上,若,则的值为( )
A. B. C. D.
3、已知向量,满足,在上的投影(正射影的数量)为-2,则的最小值为( )
A. B.10 C. D.8
4、设x,,向量,,且,则等于
A.0 B.1 C.2 D.8
5、已知向量,,且,则( )
A. B. C. D.
6、已知向量,若,则与夹角为( )
A. B. C. D.
7、在中,边上的中线的长为,若动点满足 (),则的最小值是( )
A. B. C. D.
8、已知向量若a=,b=,则|a+b|()的最小值为( )
(A) 2 (B) (C) (D)6
9、已知,,若,则( )
A. B. C. D.
10、如图,在等腰直角三角形中,设向量为边上靠近点的四等分点,过点作的垂线,点为垂线上任意一点,则( )
A. B. C. D.
11、已知四边形是平行四边形,点为边的中点,则
A. B.
C. D.
12、已知在平行四边形中,点E为的中点,设,,则( )
A. B. C. D.
二、填空题
13、已知向量a=(-2,3),b∥a,向量b的起点为A(1,2),终点B在坐标轴上,则点B的坐标为________________.
14、如图在等腰三角形ABC中,,.若D是所在平面内一点,且,设,则的最大值为________.
15、已知,若的夹角为,则__________.
16、已知在边长为2的等边中,D是BC中点, ,则_______.
三、解答题
17、(本小题满分10分)已知,若,且,求实数t的值.
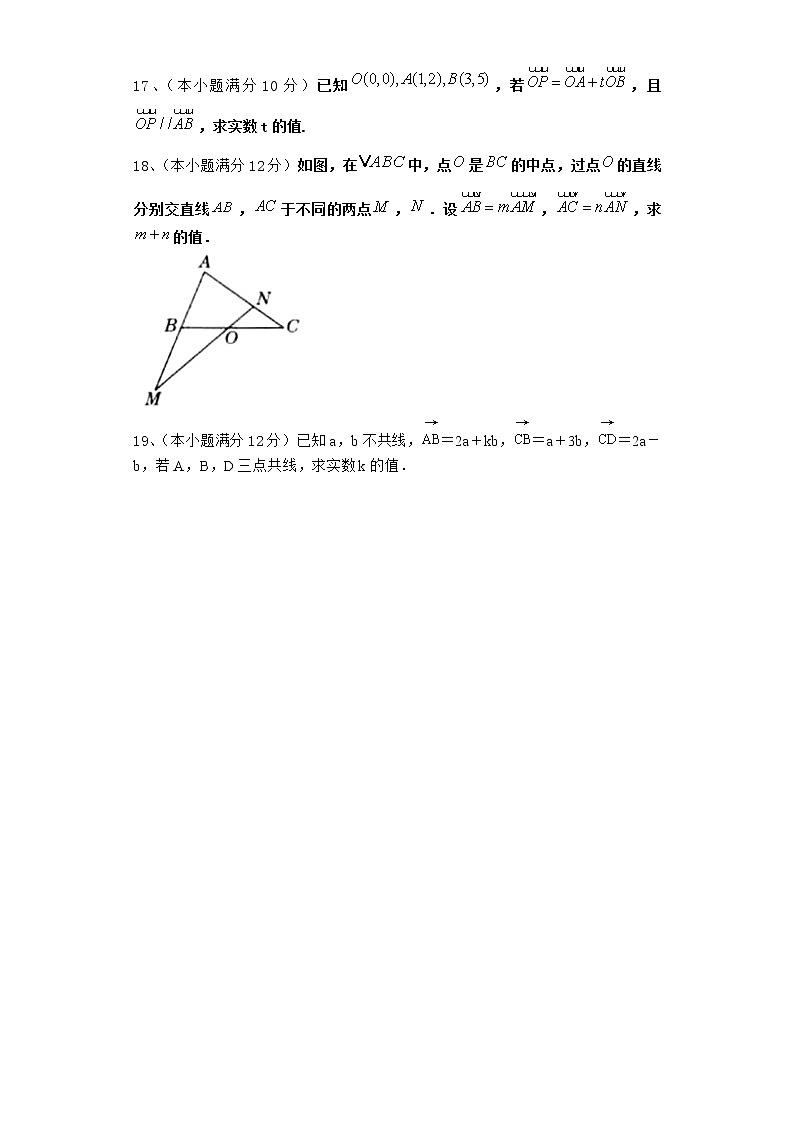
18、(本小题满分12分)如图,在中,点是的中点,过点的直线分别交直线,于不同的两点,.设,,求的值.
19、(本小题满分12分)已知a,b不共线,=2a+kb,=a+3b,=2a-b,若A,B,D三点共线,求实数k的值.
参考答案
1、答案D
解析根据直角情况分类讨论,根据向量垂直坐标表示解k的值.
详解
当A为直角时,=0,所以,
当B为直角时,=0,=0,所以,
当C为直角时,=0,=0,
所以,
综上,选D.
点睛
向量平行:,向量垂直:,向量加减:
2、答案C
解析
建立如图所示的坐标系,则, ,设, ,解得, ,则,故选C.
3、答案D
解析在上的投影(正射影的数量)为可知,可求出,求的最小值即可得出结果.
详解
因为在上的投影(正射影的数量)为,
所以,
即,而,
所以,
因为
所以,即,故选D.
点睛
本题主要考查了向量在向量上的正射影,向量的数量积,属于难题.
4、答案C
解析根据即可得出,而根据即可得出,从而得出.
详解
;
;
;
;
;
;
,.
故选:C.
点睛
考查向量垂直、平行时坐标的关系,向量坐标的数量积运算.
5、答案C
解析将转化为向量的坐标运算,得到结果.
详解
由,转化为,
根据向量数量积的坐标运算可得,解得
故选C项.
点睛
本题考查对向量之间的位置关系的转化,数量积的坐标运算,属于简单题.
6、答案A
详解:由,,
因为,,
所以方向相反,
设的夹角为,则与夹角为,
由可得,
,
所以与夹角为,故选A.
点睛:本题主要考查平行向量的性质,平面向量夹角余弦公式的应用,属于中档题. 本题主要考查向量的模及平面向量数量积公式,属于中档题.平面向量数量积公式有两种形式,一是,二是,主要应用以下几个方面:(1)求向量的夹角, (此时往往用坐标形式求解);(2)求投影, 在 上的投影是;(3)向量垂直则;(4)求向量 的模(平方后需求).
7、答案B
解析由已知条件可知三点共线,因为为中点,所以,所以=,设,则,所以,当时,取得最小值.
考点:1.三点共线的向量表示;2.向量数量积的运算.
8、答案B
解析
9、答案A
解析因为,所以,解得:.
考点:向量平行的坐标表示.
10、答案A
解析以点为原点建立直角坐标系,所以,不妨设取点,∴,故选.
考点:向量数量积
11、答案A
解析由平面向量的加法法则运算即可.
详解:如图,过E作 由向量加法的平行四边形法则可知
故选A.
点睛
本题考查平面向量的加法法则,属基础题.
12、答案A
解析利用平面向量的基本定理结合向量的加减法有,由,可得到答案.
详解:如图所示:
因为,
所以,
故选:A.
点睛
本题主要考查平面向量的基本定理以及基本运算,还考查了运算求解的能力,属于基础题.
13、答案(0,)或(,0)
解析由b∥a,可设b=λa=(-2λ,3λ).
设点B坐标为(x,y),则AB―→=(x-1,y-2)=b.
由?①
又B点在坐标轴上,则1-2λ=0或3λ+2=0,
∴λ=或λ=-,代入①式得
B点坐标为(0,)或(,0).
14、答案.
解析建立如图所示的平面直角坐标系,则,,,求得点D的轨迹方程,再利用三角函数的有界性,即可得答案;
详解:建立如图所示的平面直角坐标系,则,,.
由知,所以点D在以BC为直径的圆上.
以BC为直径的圆的方程为,
所以可设,则.
因为,,.
所以解得
所以,
其中,
所以的最大值为.
故答案为:.
点睛
本题考查平面向量基本定理的坐标运算、参数的取值范围,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力、运算求解能力,求解时注意辅助角公式和三角函数有界性的运用.
15、答案
解析
16、答案-1
解析
17、答案
详解:由,可得,
由,可得,解得.
点睛
本题主要考查了平面向量的坐标表示,以及向量的共线条件的应用,着重考查了运算与求解能力,属于基础题.
解析
18、答案
详解:解:因为是的中点,所以.
又因为,
所以.
因为,,三点共线,所以,即.
点睛
本题主要考查平面向量的应用,熟记平面向量基本定理,以及三点共线的充要条件即可,属于常考题型.
解析
19、答案∵=+=-+=a-4b,
而a与b不共线,∴≠0.
又∵A,B,D三点共线,∴,共线.
故存在实数λ,使=λ,即2a+kb=λa-4λb.
又∵a与b不共线,
∴由平面向量基本定理,得?k=-8.
解析









