初中数学冀教版八年级下册第二十二章 四边形综合与测试优秀随堂练习题

八年级数学下册第二十二章四边形综合测评

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、若菱形的周长为8，高为2，则菱形的面积为（       ）

A．2 B．4 C．8 D．16

2、如图，在中，，于E，DE交AC于点F，M为AF的中点，连接DM，若，则的大小为（       ）．

A．112° B．108° C．104° D．98°

3、下列命题中是真命题的是（       ）．A．有一组邻边相等的平行四边形是菱形 B．对角线互相垂直且相等的四边形是菱形

C．对角线相等的四边形是矩形 D．有一个角为直角的四边形是矩形

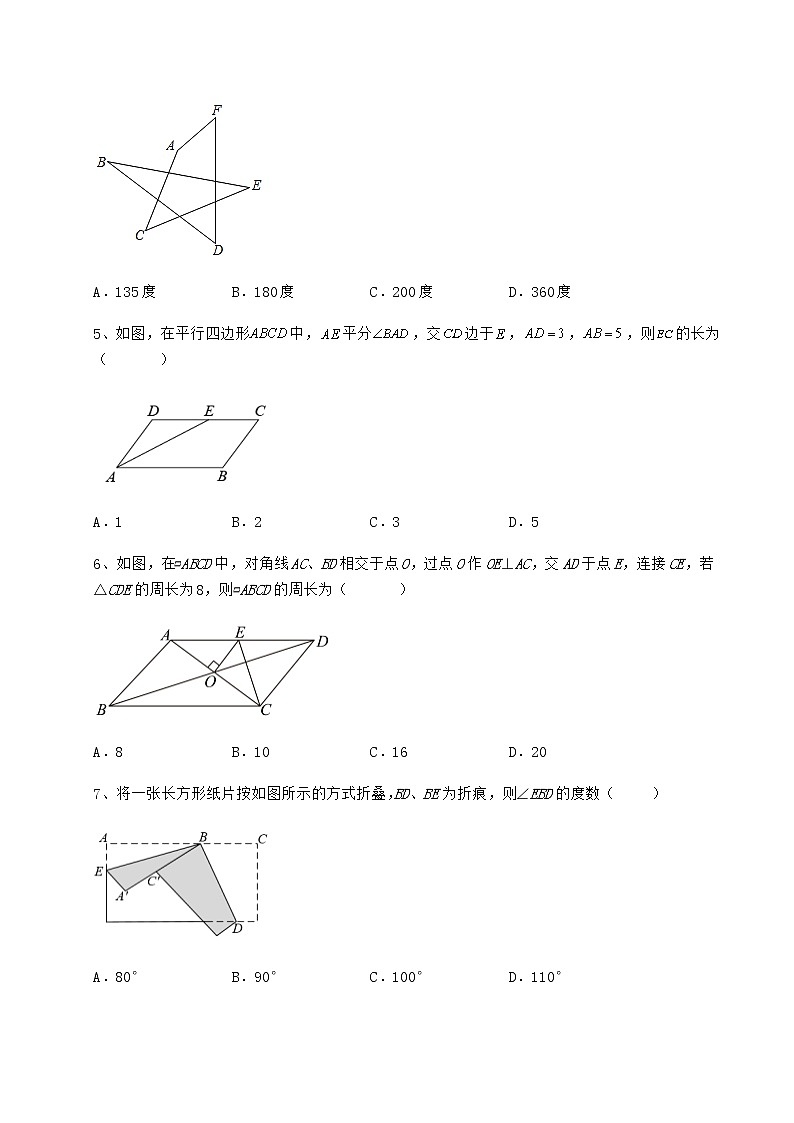
4、平面上六个点A，B，C，D，E，F，构成如图所示的图形，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F度数是（       ）

A．135度 B．180度 C．200度 D．360度

5、如图，在平行四边形中，平分，交边于，，，则的长为（       ）

A．1 B．2 C．3 D．5

6、如图，在▱ABCD中，对角线AC、BD相交于点O，过点O作OE⊥AC，交AD于点E，连接CE，若△CDE的周长为8，则▱ABCD的周长为（       ）

A．8 B．10 C．16 D．20

7、将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，则∠EBD的度数（     ）

A．80° B．90° C．100° D．110°

8、若一个正多边形的每个内角度数都为108°，则这个正多边形的边数是 (　　)

A．5 B．6 C．8 D．10

9、如图，平行四边形ABCD的对角线AC，BD相交于点O，下列结论错误的是（　　）

A．AO＝CO B．AD∥BC C．AD＝BC D．∠DAC＝∠ACD

10、下列说法错误的是（       ）

A．平行四边形对边平行且相等 B．菱形的对角线平分一组对角

C．矩形的对角线互相垂直 D．正方形有四条对称轴

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、矩形的两边长分别为3 cm和4 cm，则矩形的对角线长为_____．

2、如图，在▱ABCD中，AC是对角线，∠ACD＝90°，点E是BC的中点，AF平分∠BAC，CF⊥AF于点F，连接EF．已知AB＝5，BC＝13，则EF的长为__．

3、如图，正方形中，为上一动点（不含、，连接交于，过作交于，过作于，连接，．下列结论：①；②；③平分；④，正确的是__（填序号）．

4、矩形的性质定理1：矩形的四个角都是________．

符号语言：

∵四边形ABCD是矩形，

∴∠A＝∠B＝∠C＝∠D＝90°．

矩形的性质定理2：矩形的对角线________．

符号语言：

∵四边形ABCD是矩形，

∴AC ＝ BD．

5、如图，A、B、C均为一个正十边形的顶点，则∠ACB=_____°．

三、解答题（5小题，每小题10分，共计50分）

1、（1）【发现证明】

如图1，在正方形中，点，分别是，边上的动点，且，求证：．小明发现，当把绕点顺时针旋转90°至，使与重合时能够证明，请你给出证明过程．

（2）【类比引申】

①如图2，在正方形中，如果点，分别是，延长线上的动点，且，则（1）中的结论还成立吗？若不成立，请写出，，之间的数量关系______（不要求证明）

②如图3，如果点，分别是，延长线上的动点，且，则，，之间的数量关系是______（不要求证明）

（3）【联想拓展】如图1，若正方形的边长为6，，求的长．

2、如图，正方形ABCD中，E为BD上一点，AE的延长线交BC的延长线于点F，交CD于点H，G为FH的中点．

(1)求证：AE=CE；

(2)猜想线段AE，EG和GF之间的数量关系，并证明．

3、【问题情境】如图1，在中，，垂足为D，我们可以得到如下正确结论：①；②；③，这些结论是由古希酷著名数学家欧几里得在《几何原本》最先提出的，我们称之为“射影定理”，又称“欧几里德定理”．

(1)请证明“射影定理”中的结论③．

(2)【结论运用】如图2，正方形的边长为6，点O是对角线、的交点，点E在上，过点C作，垂足为F，连接．

①求证：．

②若，求的长．

4、如图，在矩形ABCD中，

(1)尺规作图（不写作法，保留作图痕迹）：作对角线BD的垂直平分线EF分别交AD、BC于E、F点，交BD于O点．

(2)在（1）的条件下，求证：AE=CF．

5、如图，在中，点D、E分别是边的中点，过点A作交的延长线于F点，连接，过点D作于点G．

(1)求证：四边形是平行四边形：

(2)若．

①当___________时，四边形是矩形；

②若四边形是菱形，则________．

-参考答案-

一、单选题

1、B

【解析】

【分析】

根据周长求出边长，利用菱形的面积公式即可求解．

【详解】

∵菱形的周长为8，

∴边长=2，

∴菱形的面积=2×2=4，

故选：B．

【点睛】

此题考查菱形的性质，熟练掌握菱形的面积=底×高是解题的关键．

2、C

【解析】

【分析】

根据平行四边形及垂直的性质可得为直角三角形，再由直角三角形中斜边上的中线等于斜边的一半可得，由等边对等角及三角形外角的性质得出，根据三角形内角和定理即可得出．

【详解】

解：∵四边形ABCD为平行四边形，

∴，

∵，

∴，

∴为直角三角形，

∵M为AF的中点，

∴，

∴，，

∵，

∴，

∴，

∴，

故选：C．

【点睛】

题目主要考查平行四边形的性质，直角三角形中斜边上的中线等于斜边的一半，等边对等角及三角形外角的性质和三角形内角和定理，理解题意，综合运用这些知识点是解题关键．

3、A

【解析】

【分析】

根据平行线四边形的性质得到对边相等，加上一组邻边相等，可得到四边都相等，根据菱形的定义对A、B进行判断；根据矩形的判定方法对C、D进行判断．

【详解】

解：A、平行四边形的对边相等，若有一组邻边相等，则四边都相等，所以该选项正确；

B、对角线互相平分且垂直的四边形是菱形，所以该选项不正确；

C、对角线互相平分且相等的四边形为矩形，所以该选项不正确；

D、有三个角是直角的四边形是矩形，所以该选项不正确．

故选：A．

【点睛】

本题考查了命题与定理：判断事情的语句叫命题；正确的命题叫真命题；经过证明其正确性的命题称为定理．也考查了平行四边形、矩形和菱形的判定与性质．

4、D

【解析】

【分析】

根据三角形外角性质及四边形内角和求解即可．

【详解】

解：如下图所示：

根据三角形的外角性质得，∠1=∠C+∠E，∠2=∠B+∠D，

∵∠1+∠2+∠A+∠F=360°，

∴∠A+∠B+∠C+∠D+∠E+∠F=360°，

故选：D．

【点睛】

此题考查了三角形的外角性质，熟记三角形外角性质及四边形内角和为360°是解题的关键．

5、B

【解析】

【分析】

先由平行四边形的性质得，，再证，即可求解．

【详解】

解：四边形是平行四边形，

，，

，

平分，

，

，

，

，

故选：B．

【点睛】

本题考查了平行四边形的性质，等腰三角形的判定等知识，解题的关键是灵活应用这些知识解决问题．

6、C

【解析】

【分析】

根据线段垂直平分线的判定和性质，可得AE=CE，又由CE+DE+CD=8，即AD+CD=8，继而可得ABCD的周长．

【详解】

解：∵四边形ABCD是平行四边形，

∴OA=OC，AB=CD，AD=BC，

∵OE⊥AC，

∴OE是线段AC的垂直平分线，

∴AE=CE，

∵△CDE的周长为8，

∴CE+DE+CD=8，即AD+CD =8，

∴平行四边形ABCD的周长为2(AD+CD)=16．

故选：C．

【点睛】

本题考查了平行四边形的性质、线段垂直平分线的判定和性质，关键是根据线段垂直平分线的性质进行分析．此题难度不大，注意掌握数形结合思想的应用．

7、B

【解析】

【分析】

根据翻折的性质可知，∠ABE=∠A′BE，∠DBC=∠DBC′，又∠ABE+∠A′BE+∠DBC+∠DBC′=180°，且∠EBD=∠A′BE+∠DBC′，继而即可求出答案．

【详解】

解：根据翻折的性质可知，∠ABE=∠A′BE，∠DBC=∠DBC′，

又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°，

∴∠EBD=∠A′BE+∠DBC′=180°×=90°．

故选B．

【点睛】

此题考查翻折变换的性质，三角形折叠以后的图形和原图形全等，对应的角相等，得出∠ABE=∠A′BE，∠DBC=∠DBC′是解题的关键．

8、A

【解析】

【分析】

先求出多边形的每一个外角的度数，再利用多边形的外角和即可求出答案．

【详解】

解：∵多边形的每一个内角都等于108°，多边形的内角与外角互为邻补角，

∴每个外角是：180°−108°＝72°，

∴多边形中外角的个数是360°÷72°＝5，则多边形的边数是5．

故选：A．

【点睛】

本题主要考查了多边形的外角和定理，已知外角求边数的这种方法是需要熟练掌握的内容．

9、D

【解析】

【分析】

根据平行四边形的性质解答．

【详解】

解：∵四边形ABCD是平行四边形，

∴AO＝OC，故A正确；

∴，故B正确；

∴AD＝BC，故C正确；

故选：D．

【点睛】

此题考查了平行四边形的性质，熟记平行四边形的性质是解题的关键．

10、C

【解析】

【分析】

根据矩形的性质、平行四边形的性质、菱形的性质和正方形的性质分别进行判断即可．

【详解】

解：A、平行四边形对边平行且相等，正确，不符合题意；

B、菱形的对角线平分一组对角，正确，不符合题意；

C、矩形的对角线相等，不正确，符合题意；

D、正方形有四条对称轴，正确，不符合题意；

故选：C．

【点睛】

本题考查了矩形的性质、平行四边形的性质、菱形的性质和正方形的性质，掌握以上性质定理是解题的关键．

二、填空题

1、5cm

【解析】

略

2、##3.5

【解析】

【分析】

延长AB、CF交于点H，由“ASA”可证，可得AC＝AH＝12，HF＝CF，由三角形中位线定理可求解．

【详解】

解：如图，延长AB、CF交于点H，

∵四边形ABCD是平行四边形，

∴，

∴∠ACD＝∠BAC＝90°，

∴，

∵AF平分∠BAC，

∴∠BAF＝∠CAF＝45°，

在和中，

，

∴，

∴AC＝AH＝12，HF＝CF，

∴BH＝AH﹣AB＝7，

∵点E是BC的中点，HF＝CF，

∴EF＝BH＝，

故答案为：．

【点睛】

本题考查了平行四边形的性质，全等三角形的判定和性质，勾股定理，三角形中位线的定理，添加恰当辅助线构造全等三角形是本题的关键．

3、①②④

【解析】

【分析】

连接，延长交于点．可证，进而可得，由此可得出；再由，即可得出；连接交于点，则，证明，即可得出，进而可得；过点作于点，交于点，由于是动点，的长度不确定，而是定值，即可得出不一定平分．

【详解】

解：如图，连接，延长交于点．

∵为正方形的对角线

∴，

在和中

∴

∴，

∵， ，

∴

∵，

∴

∴

∴

故①正确；

∵，

∴是等腰直角三角形

∴

故②正确；

连接交于点，则

∵

∴

在和中

∴

∴

∴

故④正确．

过点作于点，交于点，是动点

∵的长度不确定，而是定值

∴不一定等于

不一定平分

故③错误；

故答案为：①②④．

【点睛】

本题考查了正方形性质，全等三角形判定和性质，角平分线性质和判定，等腰三角形的性质与判定等，熟练掌握全等三角形判定和性质，合理添加辅助线构造全等三角形是解题关键．

4、     直角     相等

【解析】

略

5、

【解析】

【分析】

根据正多边形外角和和内角和的性质，得、；根据四边形内角和的性质，计算得；根据五边形内角和的性质，计算得，再根据三角形外角的性质计算，即可得到答案．

【详解】

如图，延长BA

∵正十边形

∴，正十边形内角，即

根据题意，得四边形内角和为：，且

∴

∴

根据题意，得五边形内角和为：，且

∴

∴

故答案为：．

【点睛】

本题考查了正多边形、三角形外角的知识；解题的关键是熟练掌握正多边形外角和、正多边形内角和的性质，从而完成求解．

三、解答题

1、（1）见解析；（2）①不成立，结论：；②，见解析；（3）

【解析】

【分析】

（1）证明，可得出，则结论得证；

（2）①将绕点顺时针旋转至根据可证明，可得，则结论得证；②将绕点逆时针旋转至，证明，可得出，则结论得证；

（3）求出，设，则，，在中，得出关于的方程，解出则可得解．

【详解】

（1）证明：把绕点顺时针旋转至，如图1，

，，，

，

，，三点共线，

，

，

，

，

，

，

，

；

（2）①不成立，结论：；

证明：如图2，将绕点顺时针旋转至，

，，，，

，

，

，

；

②如图3，将绕点逆时针旋转至，

，，

，

，

，

，

，

，

．

即．

故答案为：．

（3）解：由（1）可知，

正方形的边长为6，

，

．

，

，

设，则，，

在中，

，

，

解得：．

，

．

【点睛】

本题属于四边形综合题，主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用，解题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等进行推导．

2、 (1)见解析

(2)AE2+ GF2=EG2，证明见解析

【解析】

【分析】

（1）根据“SAS”证明△ADE≌△CDE即可；

（2）连接CG，可得CG=GF=GH=FH，再证明∠ECG=90°，然后在Rt△CEG中，可得CE2+CG2=EG2，进而可得线段AE，EG和GF之间的数量关系．

(1)

证明：∵四边形ABCD是正方形，

∴AD=CD，∠ADE=∠CDE，

在△ADE和△CDE中

，

∴△ADE≌△CDE，

∴AE=CE；

(2)

AE2+ GF2=EG2，理由：

连接CG

∵△ADE≌△CDE，

∴∠1=∠2．

∵G为FH的中点，

∴CG=GF=GH=FH，

∴∠6=∠7．

∵∠5=∠6，

∴∠5=∠7．

∵∠1+∠5=90°，

∴∠2+∠7=90°，即∠ECG=90°，

在Rt△CEG中，CE2+CG2=EG2，

∴AE2+ GF2=EG2．

【点睛】

本题考查了正方形的性质，全等三角形的判定与性质，直角三角形的性质，以及勾股定理等知识，证明△ADE≌△CDE是解（1）的关键，证明∠ECG=90°是解（2）的关键．

3、 (1)见解析；

(2)①见解析；②．

【解析】

【分析】

（1）由AA证明，再由相似三角形对应边称比例得到，继而解题；

（2）①由“射影定理”分别解得，，整理出，再结合即可证明；

②由勾股定理解得，再根据得到，代入数值解题即可．

(1)

证明：

(2)

①四边形ABCD是正方形

②在中，

在，

．

【点睛】

本题考查相似三角形的综合题，涉及勾股定理、正方形等知识，是重要考点，掌握相关知识是解题关键．

4、 (1)见解析

(2)见解析

【解析】

【分析】

（1）利用尺规作出图形即可．

（2）利用全等三角形的性质证明即可．

(1)

解：如图，直线EF即为所求作．

．

(2)

证明：在矩形ABCD中，AD=BC，∠ADB=∠DBC，

∵EF为BD的垂直平分线，

∴∠EOD=∠FOB=90°，OB=OD，

在△EOD与△FOB中，

，

∴△EOD≌△FOB（ASA），

∴ED=BF，

∴AD-ED=BC-BF，即AE=CF．

【点睛】

本题考查了作图-复杂作图，线段的垂直平分线，全等三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．

5、 (1)见解析；

(2)①3；②

【解析】

【分析】

（1）根据三角形中位线的性质得到DEAB，BD=CD，即可证得四边形ABDF是平行四边形，得到AF=BD=CD，由此得到结论；

（2）①由点D、E分别是边BC、AC的中点，得到DE=AB，由四边形是平行四边形，得到DF=2DE=AB=3，再根据矩形的性质得到AC=DF=3；

②根据菱形的性质得到DF⊥AC，推出AB⊥AC，利用勾股定理求出AC，得到CE，利用面积法求出答案．

(1)

证明：∵点D、E分别是边BC、AC的中点，

∴DEAB，BD=CD，

∵，

∴四边形ABDF是平行四边形，

∴AF=BD=CD，

∴四边形是平行四边形；

(2)

解：①∵点D、E分别是边BC、AC的中点，

∴DE=AB，

∵四边形是平行四边形，

∴DF=2DE=AB=3，

∵四边形是矩形,

∴AC=DF=3，

故答案为：3；

②∵四边形是菱形，

∴DF⊥AC，

∵DEAB，

∴AB⊥AC，

∴AD=BC=2.5，

∴AE=EC=2，

∵

∴

∴，

故答案为：．

【点睛】

此题考查了平行四边形的判定及性质，矩形的性质，菱形的性质，三角形中位线的判定及性质，勾股定理，是一道较为综合的几何题，熟练掌握各知识点并应用是解题的关键．