初中数学沪教版 (五四制)七年级下册第十五章 平面直角坐标系综合与测试练习题

七年级数学第二学期第十五章平面直角坐标系专项测评

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、若点P（m，1）在第二象限内，则点Q（1﹣m，﹣1）在（　　）

A．第四象限 B．第三象限 C．第二象限 D．第一象限

2、点A关于y轴的对称点A1坐标是（2，-1），则点A关于轴的对称点A2坐标是（　　）

A．（-1，-2） B．（-2，1） C．（2，1） D．（2，-1）

3、在平面直角坐标系xOy中，点A（2，3）关于原点对称的点的坐标是（  ）

A．（2，－3） B．（－2，3） C．（3，2） D．（－2，－3）

4、如图，是由ABO平移得到的，点A的坐标为(-1，2)，它的对应点的坐标为(3，4)，ABO内任意点P(a，b)平移后的对应点的坐标为（    ）

A．(a，b) B．(-a，-b) C．(a+2，b+4) D．(a+4，b+2)

5、在平面直角坐标系中，点的坐标是，点与点关于轴对称，则点的坐标是（    ）

A． B． C． D．

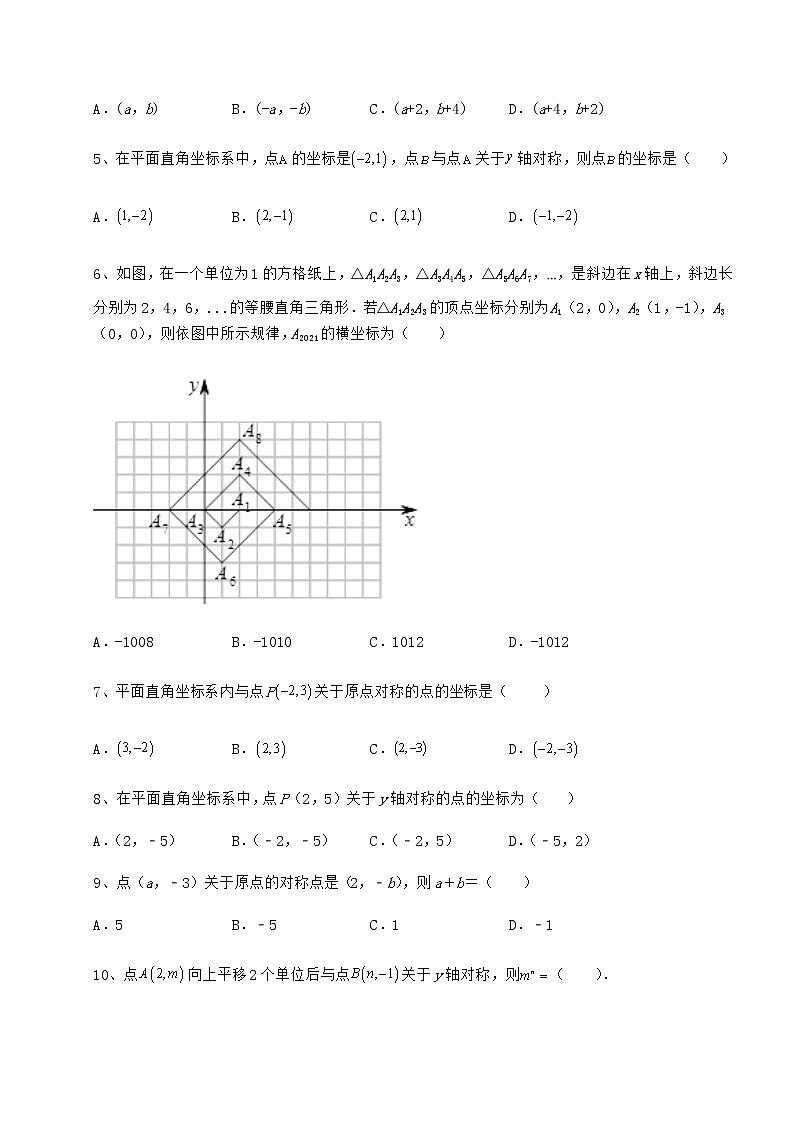
6、如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，，是斜边在x轴上，斜边长分别为2，4，6，...的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，-1），A3（0，0），则依图中所示规律，A2021的横坐标为（　　）

A．-1008 B．-1010 C．1012 D．-1012

7、平面直角坐标系内与点P关于原点对称的点的坐标是（     ）

A． B． C． D．

8、在平面直角坐标系中，点P（2，5）关于y轴对称的点的坐标为（　　）

A．（2，﹣5） B．（﹣2，﹣5） C．（﹣2，5） D．（﹣5，2）

9、点（a，﹣3）关于原点的对称点是（2，﹣b），则a＋b＝（    ）

A．5 B．﹣5 C．1 D．﹣1

10、点向上平移2个单位后与点关于y轴对称，则（    ）．

A．1 B． C． D．

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、已知点A（a﹣1，5）与点B（﹣3，b）关于x轴对称，则点C（a，b）关于y轴对称的点在第 _____象限．

2、若点在y轴上，则m=_____．

3、在平面直角坐标系中，将点绕坐标原点顺时针旋转后得到点Q，则点Q的坐标是___________．

4、已知点P（3，1）关于y轴的对称点Q的坐标为 _____．

5、若点关于原点的对称点是，则______．

三、解答题（10小题，每小题5分，共计50分）

1、如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，1），B（-1，4），C（-3，2）．

（1）画出△ABC关于y轴对称的图形△A1B1C1；

（2）如果点D（a，b）在线段AB上，请直接写出经过（1）的变化后D的对应点D1的坐标；

（3）请计算出的面积．

2、如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3）、B（﹣3，1）、C（1，3）．

（1）请按下列要求画图：

①将△ABC先向右平移4个单位长度、再向上平移2个单位长度，得到△A1B1C1，画出△A1B1C1；

②△A2B2C2与△ABC关于原点O成中心对称，画出△A2B2C2．

（2）在（1）中所得的△A1B1C1和△A2B2C2关于点M成中心对称，请写出对称中心M点的坐标 　   　．

3、已知：如图，在平面直角坐标系中．

（1）作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1三个顶点的坐标：A1（　   　），B1（　   　），C1（　   　）；

（2）直接写出△ABC的面积为　   　；

（3）在x轴上画点P，使PA+PC最小．

4、如图，三角形的项点坐标分别为，，．

（1）画出三角形关于点的中心对称的，并写出点的坐标；

（2）画出三角形绕点顺时针旋转90°后的，并写出点的坐标．

5、如图，在平面直角坐标系中，已知的三个顶点的坐标分别为、、．

（1）画出将关于点对称的图形；

（2）写出点、、的坐标．

6、如图所示，在平面直角坐标系中，已知，，．

（1）在平面直角坐标系中画出，并求出的面积；

（2）在（1）的条件下，把先关于y轴对称得到，再向下平移3个单位得到，则中的坐标分别为(      )，(      )，(      )；（直接写出坐标）

（3）已知为轴上一点，若的面积为4，求点的坐标．

7、如图，已知△ABC各顶点的坐标分别为A（-3，2），B（-4，-3），C（-1，-1）．

（1）请在图中画出△ABC关于y轴对称的△A1B1C1，

（2）并写出△A1B1C1的各点坐标．

8、如图，三个顶点的坐标分别是．

（1）请画出关于x轴对称的图形；

（2）求的面积；

（3）在x轴上求一点P，使周长最小，请画出，并通过画图求出P点的坐标．

9、如图，在平面直角坐标系中，的三个顶点均在格点上．

（1）在网格中作出关于轴对称的图形；

（2）直接写出以下各点的坐标：________，________，________；

（3）网格的单位长度为1.则________．

10、如图，在平面直角坐标系中，点B的坐标是，点C的坐标为，CB交x轴负半轴于点A，过点B作射线，作射线CD交BM于点D，且

（1）求证：点A为线段BC的中点．

（2）求点D的坐标．

-参考答案-

一、单选题

1、A

【分析】

直接利用第二象限内点的坐标特点得出m的取值范围进而得出答案．

【详解】

∵点P（m，1）在第二象限内，

∴m＜0，

∴1﹣m＞0，

则点Q（1﹣m，﹣1）在第四象限．

故选：A．

【点睛】

本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．

2、B

【分析】

由题意由对称性先求出A点坐标，再根据对称性求出点关于轴的对称点坐标．

【详解】

解：由点关于轴的对称点坐标是，可知A为，则点关于轴的对称点坐标是．

故选B．

【点睛】

本题考查对称性，利用点关于轴对称，横轴坐标变为相反数，纵轴坐标不变以及点关于轴对称，纵轴坐标变为相反数，横轴坐标不变进行分析．

3、D

【分析】

根据“关于原点对称的两个点，横坐标、纵坐标分别互为相反数”即可求得．

【详解】

解：点A（2，3）关于原点对称的点的坐标是

故选D

【点睛】

本题考查了关于原点对称的点的坐标特征，掌握“关于原点对称的两个点，横坐标、纵坐标分别互为相反数”是解题的关键．

4、D

【分析】

根据点A的坐标和点的坐标确定平移规律，即可求出点P(a，b)平移后的对应点的坐标．

【详解】

解：∵△A′B′O′是由△ABO平移得到的，点A的坐标为(-1，2)，它的对应点A′的坐标为(3，4)，

∴△ABO平移的规律是：先向右移4个单位长度，再向上平移2个单位长度，

∴△ABO内任意点P(a，b)平移后的对应点P′的坐标为(a+4，b+2)．

故选：D．

【点睛】

此题考查了平面直角坐标系中点的平移规律，解题的关键是熟练掌握平面直角坐标系中点的平移规律．点向左平移，点的横坐标减小，纵坐标不变；向右平移，点的横坐标增大，纵坐标不变；点向上平移，点的横坐标不变，纵坐标增大；向下平移，点的横坐标不变，纵坐标减小．

5、C

【分析】

根据关于轴对称的点坐标的特征：纵坐标不变，横坐标互为相反数，即可求解．

【详解】

解：点的坐标是，点与点关于轴对称，

的坐标为，

故选：C．

【点睛】

本题主要是考查了关于轴对称的点坐标的特征，熟练掌握关于坐标轴对称的点的特征，是解决该类问题的关键．

6、C

【分析】

首先确定角码的变化规律，利用规律确定答案即可．

【详解】

解：∵各三角形都是等腰直角三角形，

∴直角顶点的纵坐标的长度为斜边的一半，

A3（0，0），A7（2，0），A11（4，0）…，

∵2021÷4=505余1，

∴点A2021在x轴正半轴，纵坐标是0，横坐标是（2021+3）÷2=1012，

∴A2021的坐标为（1012，0）．

故选：C

【点睛】

本题是对点的坐标变化规律的考查，根据2021是奇数，求出点的角码是奇数时的变化规律是解题的关键．

7、C

【分析】

根据关于原点对称的点，横坐标与纵坐标都互为相反数求解即可．

【详解】

解：由题意，得

点P（-2，3）关于原点对称的点的坐标是（2，-3），

故选：C．

【点睛】

本题考查了关于原点对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．

8、C

【分析】

关于轴对称的两个点的坐标特点：横坐标互为相反数，纵坐标不变，根据原理直接可得答案.

【详解】

解：点P（2，5）关于y轴对称的点的坐标为：

故选：C

【点睛】

本题考查的是关于轴对称的两个点的坐标特点，掌握“关于轴对称的两个点的坐标特点：横坐标互为相反数，纵坐标不变”是解本题的关键.

9、B

【分析】

根据关于原点对称的点的坐标特证构造方程-b＝3，a＝−2，再解方程即可得到a、b的值，进而可算出答案．

【详解】

解：∵点（a，﹣3）关于原点的对称点是（2，﹣b），

∴−b＝3，a＝−2，

解得：b＝-3，a＝−2，

则，

故选择B．

【点睛】

本题主要考查了关于原点对称的点的坐标：掌握关于原点对称的特征，两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点是P′（−x，−y）．关键是利用对称性质构造方程．

10、D

【分析】

利用平移及关于y轴对称点的性质即可求解．

【详解】

解：把向上平移2个单位后得到点 ，

∵点与点关于y轴对称，

∴ ， ，

∴ ，

∴，

故选：D．

【点睛】

本题考查坐标与图形变化平移、轴对称的性质及负整数指数幂，解题关键是掌握平移、轴对称的性质及负整数指数幂．

二、填空题

1、四

【分析】

直接利用关于x，y轴对称点的性质得出a，b的值，进而得出答案．

【详解】

解：∵点A（a﹣1，5）与点B（﹣3，b）关于x轴对称，

∴a﹣1＝﹣3，b＝﹣5，

解得：a＝﹣2，b＝﹣5，

∴点C（a，b）为C（﹣2，﹣5），

∴点C（a，b）关于y轴对称的点的坐标为（2，﹣5），

即点C（a，b）关于y轴对称的点在第四象限．

故答案为：四．

【点睛】

本题考查了求关于坐标轴对称的点的坐标，判断点所在的象限，求得的值是解题的关键．

2、-4

【分析】

在轴上点的坐标，横坐标为，可知，进而得到的值．

【详解】

解：在轴上

故答案为：．

【点睛】

本题考察了坐标轴上点坐标的特征．解题的关键在于理解轴上点坐标的形式．在轴上点的坐标，横坐标为；在轴上点的坐标，纵坐标为．

3、

【分析】

绕坐标原点顺时针旋转即关于原点中心对称，找到关于原点中心对称的点的坐标即可，根据关于原点对称的两个点，横坐标、纵坐标分别互为相反数，即可求解．

【详解】

解：将点绕坐标原点顺时针旋转后得到点Q，则点Q的坐标是

故答案为：

【点睛】

本题考查了求一个点关于原点中心对称的点的坐标，掌握关于原点中心对称的点的坐标特征是解题的关键．关于原点对称的两个点，横坐标、纵坐标分别互为相反数．

4、（﹣3，1）

【分析】

点关于y轴的对称点坐标，横坐标为相反数，纵坐标不变；可以得到对称点Q的坐标．

【详解】

解：点P（3，1）关于y轴的对称点Q的坐标为（﹣3，1）．

故答案为：（﹣3，1）．

【点睛】

本题考察坐标系中点的对称．解题的关键在于明确点在对称时坐标的变化形式．

5、

【分析】

根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．

【详解】

解：由关于坐标原点的对称点为，得，

，

解得：

故答案为：．

【点睛】

本题考查了关于原点的对称的点的坐标，解题的关键是掌握关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．

三、解答题

1、（1）见解析；（2）（-a，b）；（3）2

【分析】

（1）分别作出点A、B、C关于y轴的对称点，再顺次连接即可得；

（2）根据（1）中规律即可得出答案；

（3）用割补法可求△ABC的面积．

【详解】

解：（1）△A1B1C1如图所示：

（2）∵D点的坐标为（a，b），

∴D1点的坐标为（-a，b）；

（3）．

【点睛】

本题考查作图-轴对称变换，三角形的面积等知识，解题的关键是掌握轴对称变换的性质，学会有分割法求三角形面积．关于y轴对称点的性质：纵坐标相同，横坐标互为相反数．

2、（1）①见解析；②见解析；（2）M（2，1）

【分析】

（1）①利用平移变换的性质分别作出A，B，C的对应点A1，B1，C1即可；

②利用中心对称的性质分别作出A，B，C的对应点A2，B2，C2即可；

（3）对应点连线的交点M即为所求．

【详解】

解：（1）①如图，△A1B1C1即为所求；

②如图，△A2B2C2即为所求；

（2）如图，点M即为所求，M（2，1），

故答案为：（2，1）．

【点睛】

本题考查作图−旋转变换，平移变换等知识，解题的关键是掌握旋转变换，平移变换的性质，属于中考常考题型．

3、（1）作图见解析，（0，﹣2），（﹣2，﹣4），（﹣4，﹣1）；（2）5；（3）见解析

【分析】

（1）直接利用轴对称图形的性质得出对应点位置进而得出答案；

（2）直接利用△ABC所在长方形面积减去周围三角形面积进而得出答案；

（3）先确定A关于轴的对称点，再连接交轴于则此时满足要求．

【详解】

解：（1）如图所示：△A1B1C1即为所求，

A1（0，﹣2），B1（﹣2，﹣4），C1（﹣4，﹣1）；

故答案为：（0，﹣2），（﹣2，﹣4），（﹣4，﹣1）；

（2）△ABC的面积为：12﹣×1×4﹣×2×2﹣×2×3＝5；

故答案为：5；

（3）如图所示：点P即为所求．

【点睛】

本题考查的是轴对称的作图，坐标与图形，掌握“利用轴对称确定线段和取最小值时点的位置”是解本题的关键.

4、（1）图见解析，；（2）图见解析，

【分析】

（1）写出，，关于原点对称的点，，，连接即可；

（2）连接OC，OB，根据旋转的90°可得，，，，，即可；

【详解】

（1），，关于原点对称的点，，，作图如下；

（2）连接OC，OB，根据旋转的90°可得，，，，，，其中点C2的坐标是（3，-1），作图如下：

【点睛】

本题主要考查了平面直角坐标系中图形的旋转，作关于原点对称的图形，准确分析作图是解题的关键．

5、（1）见解析；（2），，．

【分析】

（1）直接利用关于点O对称的性质得出对应点位置，顺次连接各个对应点，即可；

（2）根据对应点位置直接写出坐标，即可．

【详解】

解：（1）如图所示，

（2），，．

【点睛】

本题考查了利用中心对称变换在坐标系中作图，熟练掌握网格结构，准确找出对应点的位置是解题的关键．

6、（1）见解析，4；（2）0，-2，-2，-3，-4，0；（3）或．

【分析】

（1）先画出△ABC，然后再利用割补法求△ABC得面积即可；

（2）先作出，然后结合图形确定所求点的坐标即可；

（3）先求出PB的长，然后分P在B的左侧和右侧两种情况解答即可．

【详解】

解：（1）画出如图所示：

的面积是：；

（2）作出如图所示，则(0，-2)，( -2，-3)，(-4，0)

故填：0，-2，-2，-3，-4，0；

（3）∵P为x轴上一点，的面积为4，

∴，

∴当P在B的右侧时，横坐标为：

当P在B的左侧时，横坐标为，

故P点坐标为：或．

【点睛】

本题主要考查了轴对称、三角形的平移、三角形的面积以及平面直角坐标系中点的坐标等知识点，根据题意画出图形成为解答本题的关键．

7、（1）见解析；（2）A1（3，2），B1（4，-3），C1（1，-1）．

【分析】

（1）分别作出三个顶点关于y轴的对称点，再首尾顺次连接即可；

（2）根据所作图形可得答案．

【详解】

解：（1）如图所示，△A1B1C1即为所求作．

（2）由图可知，A1（3，2），B1（4，-3），C1（1，-1）．

【点睛】

本题主要考查作图-轴对称变换，解题的关键是掌握轴对称变换的定义和性质，并据此得出变换后的对应点．注意：关于x轴对称的点，横坐标相同，纵坐标互为相反数．

8、（1）见解析；（2）3.5；（3）图形见解析，P点的坐标为

【分析】

（1）找到关于轴对称的点，顺次连接，则即为所求；

（2）根据网格的特点，根据即可求得的面积；

（3）连接，与轴交于点，根据对称性即可求得，点即为所求．

【详解】

解：（1）找到关于轴对称的点，顺次连接，则即为所求，如图

（2）

（3）根据作图可知，P点的坐标为

【点睛】

本题考查了画轴对称图形，坐标与图形，轴对称的性质求线段和的最小值，掌握轴对称的性质是解题的关键．

9、（1）见解析；（2）；； ；（3）5

【分析】

（1）利用轴对称的性质分别作出A，B，C的对应点A1，B1，C1即可；

（2）根据点的位置写出坐标即可；

（3）把三角形的面积看成矩形面积减去周围三个三角形面积即可．

【详解】

解：（1）如图，△A1B1C1即为所求；

（2）A1（3，4），B1（5，2），C1（2，0）．

故答案为：（3，4），（5，2），（2，0）；

（3）网格的单位长度为1，则=3×4-×2×3-×2×2-×1×4=5，

故答案为：5．

【点睛】

本题考查轴对称，三角形的面积等知识，解题的关键是掌握轴对称的性质，学会利用分割法求三角形面积．

10、（1）证明见解析，（2）（8，2）．

【分析】

（1）过点C作CQ⊥OA于Q，证△CQA≌△BOA，即可证明点A为线段BC的中点；

（2）过点C作CR⊥OB于R，过点D作DS⊥OB于S，证△CRB≌△BSD，根据全等三角形对应边相等即可求点D的坐标．

【详解】

（1）证明：过点C作CQ⊥OA于Q，

∵点B的坐标是，点C的坐标为，

∴CQ=OB=4，

∵∠CQO＝∠BOA＝90°，∠CAQ＝∠BAO，

∴△CQA≌△BOA，

∴CA=AB，

∴点A为线段BC的中点．

（2）过点C作CR⊥OB于R，过点D作DS⊥OB于S，

∵，

∴∠CRB＝∠DSB＝∠CBD＝90°，

∴∠CBR+∠SBD＝90°，∠SDB+∠SBD＝90°，

∴∠CBR＝∠SDB，

∵，

∴∠BCD＝∠BDC＝45°，

∴CB=DB，

∴△CRB≌△BSD，

∴CR=SB，RB=DS，

∵点B的坐标是，点C的坐标为，

∴CR=SB＝6，RB=DS＝8，

∴OS=SB－OB＝2，

点D的坐标为（8，2）．

【点睛】

本题考查了全等三角形的判定与性质和点的坐标，解题关键是树立数形结合思想，恰当作辅助线，构建全等三角形．