沪教版 (五四制)七年级下册第十五章 平面直角坐标系综合与测试练习题

这是一份沪教版 (五四制)七年级下册第十五章 平面直角坐标系综合与测试练习题，共28页。试卷主要包含了若点在第三象限，则点在．，在平面直角坐标系中，点A等内容，欢迎下载使用。
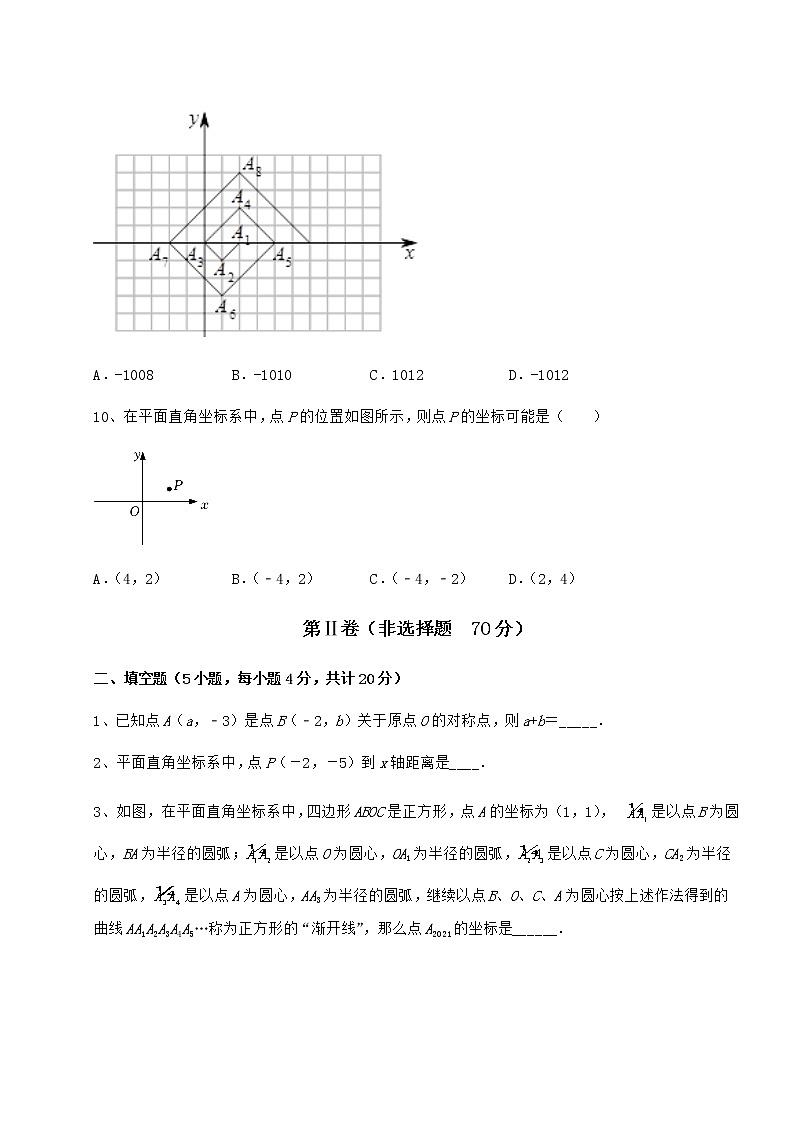
七年级数学第二学期第十五章平面直角坐标系定向训练 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图为某停车场的平面示意图，若“奥迪”的坐标是（-2，-1），“奔驰”的坐标是（1，-1），则“东风标致”的坐标是（  ）A．（-3，2） B．（3，2） C．（-3，-2） D．（3，-2）2、在平面直角坐标系中，点的坐标为，将点向左平移个单位长度，再向上平移个单位长度得到点，则点的坐标为（ ）A． B． C． D．3、点P在第二象限内，P点到x、y轴的距离分别是4、3，则点P的坐标为（　　）A．（－4，3） B．（－3，－4） C．（－3，4） D．（3，－4）4、在平面直角坐标系中，点关于轴的对称点的坐标是（    ）A． B． C． D．5、上海是世界知名金融中心，以下能准确表示上海市地理位置的是(   )A．在中国的东南方 B．东经，北纬 C．在中国的长江出海口 D．东经．6、若点在第三象限，则点在（    ）．A．第一象限 B．第二象限 C．第三象限 D．第四象限7、在平面直角坐标系中，点A（0，3），B（2，1），经过点A的直线l∥x轴，C是直线l上的一个动点，当线段BC的长度最短时，点C的坐标为（　　）A．（0，1） B．（2，0） C．（2，﹣1） D．（2，3）8、点向上平移4个单位，再向左平移3个单位到点B，则点B的坐标为（    ）A． B． C． D．9、如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，，是斜边在x轴上，斜边长分别为2，4，6，...的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，-1），A3（0，0），则依图中所示规律，A2021的横坐标为（　　）A．-1008 B．-1010 C．1012 D．-101210、在平面直角坐标系中，点P的位置如图所示，则点P的坐标可能是（    ）A．（4，2） B．（﹣4，2） C．（﹣4，﹣2） D．（2，4）第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、已知点A（a，﹣3）是点B（﹣2，b）关于原点O的对称点，则a+b＝_____．2、平面直角坐标系中，点P（－2，－5）到x轴距离是____．3、如图，在平面直角坐标系中，四边形ABOC是正方形，点A的坐标为（1，1），是以点B为圆心，BA为半径的圆弧；是以点O为圆心，OA1为半径的圆弧，是以点C为圆心，CA2为半径的圆弧，是以点A为圆心，AA3为半径的圆弧，继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”，那么点A2021的坐标是______．4、已知点与点关于原点对称，则a-b的值为________．5、若，其中b，c为常数，则点P（b，c）关于x轴的对称点的坐标为____．三、解答题（10小题，每小题5分，共计50分）1、如图，在平面直角坐标系中，已知的三个顶点都在网格的格点上．（1）在图中作出关于轴对称的，并写出点的对应点的坐标；（2）在图中作出关于轴对称的，并写出点的对应点的坐标．2、已知点A（1，﹣1），B（﹣1，4），C（﹣3，1）．（1）请在如图所示的平面直角坐标系中（每个小正方形的边长都为1）画出△ABC；（2）作△ABC关于x轴对称的△DEF，其中点A，B，C的对应点分别为点D，E，F；（3）连接CE，CF，请直接写出△CEF的面积．3、如图，在直角坐标系中，A(－1，5)，B(－3，0)，C(－4，3)．(1)在图中作出△ABC关于y轴对称的图形△A1B1C1；(2)写出点A1　　　　　，B1　　　　　，C1　　　　　的坐标．4、如图，已知△ABC各顶点的坐标分别为A（-3，2），B（-4，-3），C（-1，-1）． （1）请在图中画出△ABC关于y轴对称的△A1B1C1，（2）并写出△A1B1C1的各点坐标．5、如图，方格图中每个小正方形的边长为1，点A，B，C都是格点．（1）画出△ABC关于直线MN对称的．（2）若B为坐标原点，请写出、、的坐标，并直接写出的长度．．（3）如图2，A，C是直线同侧固定的点，D是直线MN上的一个动点，在直线MN上画出点D，使最小．（保留作图痕迹）6、△ABC在平面直角坐标系中的位置如图所示，已知A（﹣2，3），B（﹣3，1），C（﹣1，2）．（1）画出△ABC绕点O逆时针旋转90°后得到的△A1B1C1；（2）画出△ABC关于原点O的对称图形△A2B2C2；（3）直接写出下列点的坐标：A1　 　，B2　   　．7、在平面直角坐标系中，的顶点，，的坐标分别为，，．与关于轴对称，点，，的对应点分别为，，．请在图中作出，并写出点，，的坐标．8、如图，已知的三个顶点分别为，，．（1）请在坐标系中画出关于轴对称的图形（，，的对应点分别是，，），并直接写出点，，的坐标；（2）求四边形的面积．9、在如图所示的平面直角坐标系中，A点坐标为．（1）画出关于y轴对称的；（2）求的面积．10、如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）．（1）请画出△ABC关于y轴对称的△A1B1C1，并写出点A1的坐标；（2）请画出△ABC绕点B顺时针旋转90°后的△A2BC2；（3）求出（2）中△A2BC2的面积． -参考答案-一、单选题1、D【分析】由题意，先建立平面直角坐标系，确定原点的位置，即可得到“东风标致”的坐标．【详解】解：∵“奥迪”的坐标是（2，1），“奔驰”的坐标是（1，1），∴建立平面直角坐标系，如图所示：∴“东风标致”的坐标是（3，2）；故选：D．【点睛】本题考查了坐标确定位置：平面坐标系中的点与有序实数对一一对应；记住平面内特殊位置的点的坐标特征．2、A【分析】利用平移中点的变化规律：横坐标右移加，左移减；纵坐标上移加，下移减求解即可．【详解】解：∵点A的坐标为（2，1），将点A向左平移3个单位长度，再向上平移1个单位长度得到点A′，∴点A′的横坐标是2-3=-1，纵坐标为1+1=2，即（-1，2）．故选：A．【点睛】本题考查图形的平移变换，关键是要懂得左右移动改变点的横坐标，左减、右加；上下移动改变点的纵坐标，下减、上加．3、C【分析】点P到x、y轴的距离分别是4、3，表明点P的纵坐标、横坐标的绝对值分别为4与3，再由点P在第二象限即可确定点P的坐标．【详解】∵P点到x、y轴的距离分别是4、3，∴点P的纵坐标绝对值为4、横坐标的绝对值为3，∵点P在第二象限内，∴点P的坐标为（－3，4），故选：C．【点睛】本题考查了平面直角坐标系中点所在象限的特点，点到的坐标轴的距离，确定点的坐标，掌握这些知识是关键．要注意：点到x、y轴的距离是此点的纵坐标、横坐标的绝对值，而非横坐标、纵坐标的绝对值．4、B【分析】根据关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数可得答案．【详解】解：点P（2，-1）关于x轴的对称点的坐标为（2，1），故选：B．【点睛】此题主要考查了关于x轴的对称点的坐标，关键是掌握点的坐标的变化规律．5、B【分析】根据有序数对的性质解答．【详解】解：能准确表示上海市地理位置的是东经，北纬，故选：B．【点睛】此题考查了表示平面上点的位置的方法：有序数对，需用两个有序数量来表示某一位置，掌握有序数对的性质是解题的关键．6、A【分析】根据第三象限点的横坐标与纵坐标都是负数，然后判断点Q所在的象限即可．【详解】∵点P（m，n）在第三象限，∴m＜0，n＜0，∴-m＞0，-n＞0，∴点在第一象限．故选：A．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．7、D【分析】根据垂线段最短可知BC⊥l，即BC⊥x轴，由已知即可求解．【详解】解：∵点A（0，3），经过点A的直线l∥x轴，C是直线l上的一个动点，∴点C的纵坐标是3，根据垂线段最短可知，当BC⊥l时，线段BC的长度最短，此时， BC⊥x轴，∵B（2，1），∴点C的横坐标是2，∴点C坐标为（2，3），故选：D．【点睛】本题考查坐标与图形、垂线段最短，熟知图形与坐标的关系，掌握垂线段最短是解答的关键．8、C【分析】利用平移中点的变化规律：横坐标右移加，左移减；纵坐标上移加，下移减求解即可．【详解】解：点A的坐标为（3，5），将点A向上平移4个单位，再向左平移3个单位到点B，点B的横坐标是：33=6，纵坐标为：5+4=1，即（6，1）．故选：C．【点睛】本题考查图形的平移变换，关键是要懂得左右移动改变点的横坐标，左减、右加；上下移动改变点的纵坐标，下减、上加．9、C【分析】首先确定角码的变化规律，利用规律确定答案即可．【详解】解：∵各三角形都是等腰直角三角形，∴直角顶点的纵坐标的长度为斜边的一半，A3（0，0），A7（2，0），A11（4，0）…，∵2021÷4=505余1，∴点A2021在x轴正半轴，纵坐标是0，横坐标是（2021+3）÷2=1012，∴A2021的坐标为（1012，0）．故选：C【点睛】本题是对点的坐标变化规律的考查，根据2021是奇数，求出点的角码是奇数时的变化规律是解题的关键．10、A【分析】根据点在第一象限，结合第一象限点的横纵坐标都为正的进而即可判断【详解】解：由题意可知，点P在第一象限，且横坐标大于纵坐标，A．（4，2）在第一象限，且横坐标大于纵坐标，故本选项符合题意；B．（﹣4，2）在第二象限，故本选项符合题意；C．（﹣4，﹣2）在第三象限，故本选项符合题意；D．（2，4）在第一象限，但横坐标小于纵坐标，故本选项符合题意；故选：A．【点睛】本题考查了各象限点的坐标特征，掌握各象限点的坐标特征是解题的关键．平面直角坐标系中各象限点的坐标特点：①第一象限的点：横坐标>0，纵坐标>0；②第二象限的点：横坐标<0，纵坐标>0；③第三象限的点：横坐标<0，纵坐标<0；④第四象限的点：横坐标>0，纵坐标<0．二、填空题1、5【分析】根据关于原点对称的点的特点可得a，b的值，相加即可．【详解】解：∵点A（a，﹣3）是点B（﹣2，b）关于原点O的对称点，∴a＝2，b＝3，∴a+b＝5．故答案为5．【点睛】本题考查了关于原点对称的点的特点，掌握“关于原点对称的两个点，横坐标、纵坐标分别互为相反数”是解题的关键．2、5【分析】根据点到x轴的距离等于纵坐标的绝对值解答即可．【详解】解：点P（-2，-5）到x轴的距离是5．故答案为：5．【点睛】本题考查了点到坐标轴的距离，熟记点到x轴的距离等于纵坐标的绝对值是解题的关键．3、（2021，0）【分析】将四分之一圆弧对应的A点坐标看作顺时针旋转90°，再根据A、A1、A2、A3、A4的坐标找到规律即可．【详解】∵A点坐标为（1，1），且A1为A点绕B点顺时针旋转90°所得∴A1点坐标为（2，0）又∵A2为A1点绕O点顺时针旋转90°所得∴A2点坐标为（0，-2）又∵A3为A2点绕C点顺时针旋转90°所得∴A3点坐标为（-3，1）又∵A4为A3点绕A点顺时针旋转90°所得∴A4点坐标为（1，5）由此可得出规律：An为绕B、O、C、A四点作为圆心依次循环顺时针旋转90°，且半径为1、2、3、、、n，每次增加1．∵2021÷4=505…1故A2021为以点B为圆心，半径为2021的A2020点顺时针旋转90°所得故A2021点坐标为（2021，0）．故答案为：（2021，0）．【点睛】本题考查了点坐标规律探索，通过点的变化探索出旋转的规律是解题的关键．4、5【分析】直接利用关于原点对称点的性质得出a，b的值，代入求解即可．【详解】解：∵点A（a，1）与点B（﹣4，b）关于原点对称，∴，，∴，故答案为：5．【点睛】本题考查了关于原点对称点的性质及求代数式的值，正确得出a，b的值是解题的关键．5、（-1，6）【分析】先利用多项式的乘法展开再根据对应项系数相等确定出b、c的值，然后根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答．【详解】解：∵（x+2）（x-3）=x2-x-6，∴b=-1，c=-6，∴点P的坐标为（-1，-6），∴点P（-1，-6）关于x轴对称点的坐标是（-1，6）．故答案为：（-1，6）．【点睛】本题考查了多项式的乘法，关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．三、解答题1、（1）为所求，图形见详解，点B1（-5，-1）；（2）为所求，图形见详解，点B2（5，1）．【分析】（1）根据关于轴对称的，求出A1（-6，-6），B1（-5，-1），C1（-1，-6），然后在平面直角坐标系中描点，顺次连接A1B1， B1C1，C1A1即可；（2）根据关于轴对称的，求出A2（6，6），点B2（5，1），点C2（1，6），然后在平面直角坐标系中描点，顺次连接A2B2， B2C2，C2A2即可．【详解】解：（1）根据点在平面直角坐标系中的位置，△ABC三点坐标分别为A（-6，6），B（-5，1），C（-1，6），关于轴对称的，关于x轴对称点的特征是横坐标不变，纵坐标互为相反数，∴中点A1（-6，-6），点B1（-5，-1），点C1（-1，-6），在平面直角坐标系中描点A1（-6，-6），B1（-5，-1），C1（-1，-6），顺次连接A1B1， B1C1，C1A1，则为所求，点B1（-5，-1）；（2）∵关于轴对称的，∴点的坐标特征是横坐标互为相反数，纵坐标不变，∵△ABC三点坐标分别为A（-6，6），B（-5，1），C（-1，6），∴中点A2（6，6），点B2（5，1），点C2（1，6），在平面直角坐标系中描点A2（6，6），B2（5，1），C2（1，6），顺次连接A2B2， B2C2，C2A2，则为所求，点B2（5，1）．【点睛】本题考查在平面直角坐标系中画称轴对称的图形，掌握画图方法，先求坐标，描点，顺次连接是解题关键．2、（1）作图见详解；（2）作图见详解；（3）的面积为2．【分析】（1）直接在坐标系中描点，然后依次连线即可；（2）先确定A、B、C三点关于x轴对称的点的坐标，然后依次连接即可；（3）根据三角形在坐标系中的位置，确定三角形的底和高，直接求面积即可．【详解】解：（1）如图所示，即为所求；（2）A、B、C三点关于x轴对称的点的坐标分别为：，，，然后描点、连线，∴即为所求；（3）由图可得：，∴的面积为2．【点睛】题目主要考查在坐标系中作轴对称图形及点的坐标特点，熟练掌握轴对称图形的性质是解题关键．3、（1）见解析；（2）（1，5），（3，0），（4，3）【分析】（1）根据对称性即可在图中作出△ABC关于y轴对称的图形△A1B1C1；（2）结合（1）即可写出点A1，B1，C1的坐标．【详解】解：（1）如图，△A1B1C1即为所求；（2）A1（1，5），B1（3，0），C1（4，3）；故答案为：（1，5），（3，0），（4，3）．【点睛】本题考查了作图-轴对称变换，解决本题的关键是掌握轴对称性质．关于y轴对称的点的坐标特点：横坐标互为相反数，纵坐标相同．4、（1）见解析；（2）A1（3，2），B1（4，-3），C1（1，-1）．【分析】（1）分别作出三个顶点关于y轴的对称点，再首尾顺次连接即可；（2）根据所作图形可得答案．【详解】解：（1）如图所示，△A1B1C1即为所求作．（2）由图可知，A1（3，2），B1（4，-3），C1（1，-1）．【点睛】本题主要考查作图-轴对称变换，解题的关键是掌握轴对称变换的定义和性质，并据此得出变换后的对应点．注意：关于x轴对称的点，横坐标相同，纵坐标互为相反数．5、（1）画图见解析；（2），；（3）画图见解析【分析】（1）分别确定关于对称的对称点 再顺次连接从而可得答案；（2）根据在坐标系内的位置直接写其坐标与的长度即可；（3）先确定关于的对称点，再连接 交于 则 从而可得答案.【详解】解：（1）如图1，是所求作的三角形，（2）如图1，为坐标原点，则  （3）如图2，点即为所求作的点.【点睛】本题考查的是画轴对称图形，建立坐标系，用根据点的位置确定点的坐标，轴对称的性质，掌握“利用轴对称的性质得到两条线段和取最小值时点的位置”是解本题的关键.6、（1）见解析；（2）见解析；（3）（-3，-2），（3，-1）【分析】（1）先根据网格找到A、B、C的对应点A1、B1、C1，然后顺次连接A1、B1、C1即可；（2）先根据网格找到A、B、C的对应点A2、B2、C2，然后顺次连接A2、B2、C2即可；（3）根据（1）（2）说画图形求解即可．【详解】解：（1）如图所示，即为所求；（2）如图所示，即为所求；（3）由图可知，的坐标为（-3，-2），的坐标为（3，-1），故答案为：（-3，-2）；（3，-1）．【点睛】本题主要考查了坐标与图形变化—旋转变化，轴对称变化，画旋转图形和轴对称图形，解题的关键在于能够熟练掌握相关知识进行求解．7、作图见解析，点，点，点【分析】分别作出A，B，C的对应点，，即可．【详解】解： 如图所示．点，点，点．【点睛】本题考查了作图-轴对称变换，直角坐标系中表示点的坐标，熟知关于y轴对称的点的坐标特点是解答此题的关键．8、（1）画图见解析，，，；（2）【分析】（1）根据关于轴对称的点的坐标特征写出点，，的坐标，然后描点即可；（2）根据三角形面积公式，利用四边形的面积进行计算．【详解】解：（1）根据题意得：点，，关于轴的对称点分别为，，，如图，为所作；（2）四边形的面积．【点睛】本题主要考查了图形的变换——轴对称，坐标与图形，熟练掌握轴对称图形的关键是找到对称轴，图形关于对称轴折叠前后对应线段，对应角相等是解题的关键．9、（1）见解析；（2）．【分析】（1）分别作A、B、C三点关于y轴的对称点A1、B1、C1，顺次连接A1、B1、C1即可得答案；（2）用△ABC所在矩形面积减去三个小三角形面积即可得答案．【详解】（1）分别作A、B、C三点关于y轴的对称点A1、B1、C1，△A1B1C1即为所求；（2）S△ABC=3×3=．【点睛】本题考查了作轴对称图形和运用拼凑法求不规则三角形的面积，其中掌握拼凑法求不规则图形的面积是解答本题的关键．10、（1）见解析，（﹣2，4）；（2）见解析；（3）3.5【分析】（1）利用关于y轴对称的点的坐标特征写出A、B、C的对应点A1、B1、C1的坐标，然后描点即可；（2）利用网格特点和旋转的性质画出A、C的对应点A2和C2即可；（3）用一个矩形的面积分别减去三个直角三角形的面积去计算△A2BC2的面积．【详解】解：（1）如图，△A1B1C1为所作，点A1的坐标为（﹣2，4）；（2）如图，△A2BC2为所作；（3）△A2BC2的面积＝3×3﹣×3×1﹣×2×1﹣×3×2＝3.5．【点睛】本题考查了作图−旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了轴对称变换．