初中数学沪教版 (五四制)七年级下册第十二章 实数综合与测试课时练习

沪教版（上海）七年级数学第二学期第十二章实数专项攻克

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、下列各数中，最小的数是（    ）

A．0 B． C． D．﹣3

2、若 ,则 （   ）

A． B． C． D．

3、在0.1010010001…（相邻两个1之间依次多一个0），，，中，无理数有（    ）

A．1个 B．2个 C．3个 D．4个

4、下列各数中，3.1415，，，0.321，π，2.32232223…（相邻两个3之间的2的个数逐次增加1），无理数有（    ）

A．0个 B．1个 C．2个 D．3个

5、已知a＝，b＝－|－|，c＝（－2）3，则a，b，c的大小关系是（    ）

A．b＜a＜c B．b＜c＜a C．c＜b＜a D．a＜c＜b

6、实数在哪两个连续整数之间（    ）

A．3与4 B．4与5 C．5与6 D．12与13

7、9的平方根是（　　）

A．±9 B．9 C．±3 D．3

8、下列各数是无理数的是（    ）

A． B．3.33 C． D．

9、实数2，0，﹣3，﹣中，最小的数是（　　）

A．﹣3 B．﹣ C．2 D．0

10、的算术平方根是（    ）

A．2 B． C． D．

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、的平方根是________．

2、计算： = ______．

3、的整数部分是_____________．

4、计算______．

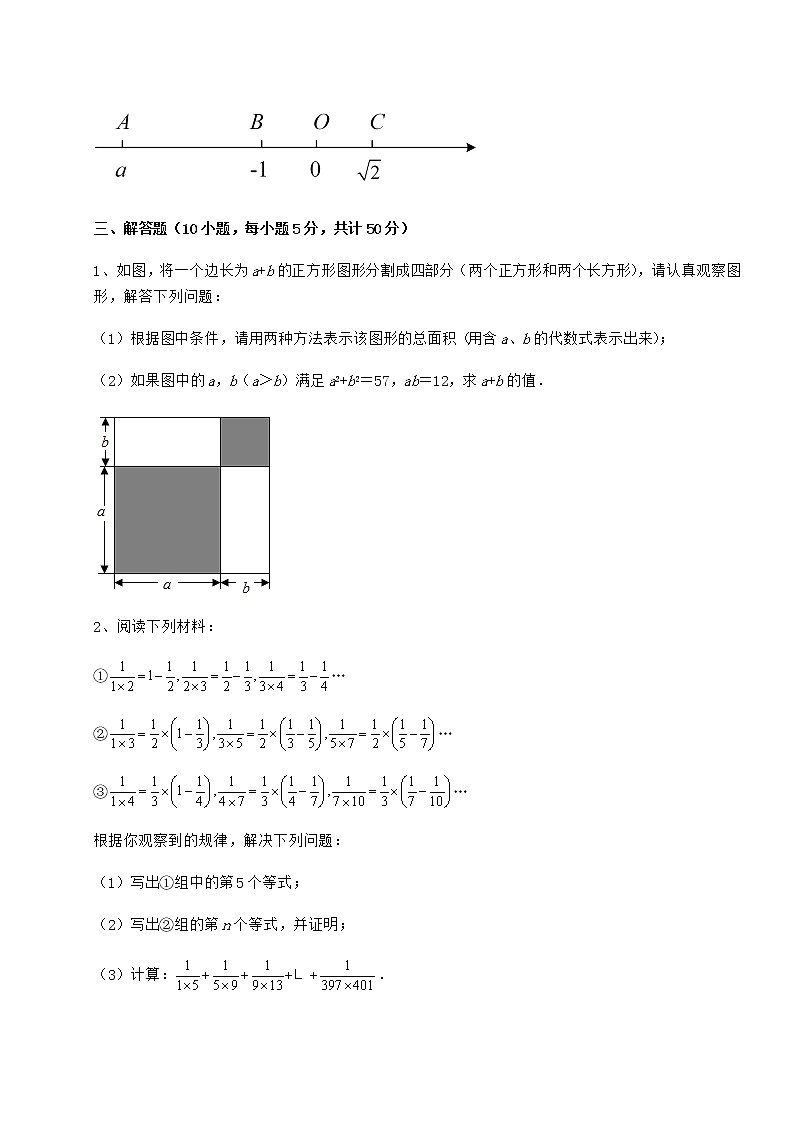
5、如图，A，B，C在数轴上对应的点分别为a，﹣1，，其中a＜﹣1，且AB＝BC，则|a|＝_____．

三、解答题（10小题，每小题5分，共计50分）

1、如图，将一个边长为a+b的正方形图形分割成四部分（两个正方形和两个长方形），请认真观察图形，解答下列问题：

（1）根据图中条件，请用两种方法表示该图形的总面积（用含a、b的代数式表示出来）；

（2）如果图中的a，b（a＞b）满足a2+b2＝57，ab＝12，求a+b的值．

2、阅读下列材料：

①…

②…

③…

根据你观察到的规律，解决下列问题：

（1）写出①组中的第5个等式；

（2）写出②组的第n个等式，并证明；

（3）计算：．

3、计算题

（1）；

（2）（﹣1）2021＋．

4、（1）计算：；

（2）分解因式：．

5、做一个底面积为24cm2，长、宽、高的比为4：2：1的长方体，求这个长方体的长、宽、高分别是多少cm？

6、直接写出结果：

（1）____________；

（2）____________；

（3）的立方根＝____________；

（4）若x2＝（﹣7）2，则x＝____________．

7、计算：（1）；

（2）．

8、已知a2＝16，b3＝27，求ab的值．

9、求方程中x 的值（x﹣1）2 ﹣16 = 0

10、（1）计算：﹣32﹣（2021）0+|﹣2|﹣（）﹣2×（﹣）；

（2）解方程：＝﹣1．

-参考答案-

一、单选题

1、C

【分析】

有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．

【详解】

解：，

所给的各数中，最小的数是．

故选：C．

【点睛】

本题主要考查了有理数大小比较的方法，解题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．

2、B

【分析】

先利用的值，求出，再利用负整数指数幂的运算法则，得到的值．

【详解】

解：，

或（舍去），

，

故选：B．

【点睛】

本题主要是考查了开二次根式以及负整数指数幂的运算法则，熟练掌握负整数指数幂的运算法则：，是解决本题的关键．

3、B

【分析】

无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．

【详解】

解：0.1010010001…（相邻两个1之间依次多一个0），是无限不循环小数，是无理数；

是有理数；

是有理数；

是无理数；

∴无理数有2个，

故选B．

【点睛】

本题主要考查了无理数的定义，解题的关键在于能够熟练掌握有理数和无理数的定义．

4、D

【分析】

理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．

【详解】

3.1415，0.321是有限小数，属于有理数；

是分数，属于有理数；

无理数有，π，2.32232223…（相邻两个3之间的2的个数逐次增加1），共3个．

故选：D．

【点睛】

此题考查了无理数．解题的关键是掌握实数的分类．

5、C

【分析】

本题主要是根据乘方、绝对值、负指数幂的运算进行求值，比较大小，负指数幂运算是根据：“底倒指反”，进行转化之后再化简，即：a=2；绝对值化简先判断绝对值内的数是正数还是负数，正数的绝对值是它本身，负数的绝对值是它的相反数，在进行化简，即b=；乘方运算中，负数的奇次幂还是负数，即：c=-8，据此进行数据的比较．

【详解】

解：由题意得：a===４，b==，c＝＝-8，

∴c＜b＜a．

故选：C．

【点睛】

本题主要考查的是乘方、绝对值、负指数幂的基础运算，熟练掌握其运算以及符号是解本题的关键．

6、B

【分析】

估算即可得到结果．

【详解】

解：，

，

故选：B．

【点睛】

本题考查了估算无理数的大小，解题的关键是熟练掌握估算无理数的大小的法则．

7、C

【分析】

根据平方根的定义解答即可．

【详解】

解：∵（±3）2＝9，

∴9的平方根是±3．

故选：C．

【点睛】

此题考查了平方根的定义，解题的关键是熟练掌握平方根的定义．如果一个数的平方等于a，即，那么这个数叫做a的平方根．正数有两个平方根，且互为相反数，其中正的那个数也叫算数平方根，0的平方根和算数平方根都是0，负数没有平方根，也没有算术平方根．

8、C

【分析】

无理数是指无限不循环小数，由此概念以及立方根的定义分析即可．

【详解】

解：，是有理数，3.33和是有理数，是无理数，

故选：C．

【点睛】

本题考查求一个数的立方根，以及无理数的识别，掌握立方根的定义以及无理数的基本定义是解题关键．

9、A

【分析】

根据实数的性质即可判断大小．

【详解】

解：∵﹣3＜﹣＜0＜2

故选A．

【点睛】

此题主要考查实数的大小比较，解题的关键是熟知实数的性质．

10、A

【分析】

根据算术平方根的定义即可求出结果．

【详解】

解：=4，4的算术平方根是2．

故选：A．

【点睛】

此题主要考查了算术平方根的定义．一个正数的算术平方根就是其正的平方根．

二、填空题

1、±

【分析】

直接根据平方根的定义求解即可．

【详解】

解：的平方根为±=±．

故答案为：±．

【点睛】

本题主要考查了平方根，知道一个正数有两个平方根是解决本题的关键．

2、##

【分析】

根据求一个数的立方根，化简绝对值，求一个数的算术平方根，进行实数的混合运算

【详解】

解：

故答案为：

【点睛】

本题考查了一个数的立方根，化简绝对值，求一个数的算术平方根，掌握以上知识是解题的关键．

3、3

【分析】

先估算的近似值，然后进行计算即可．

【详解】

解：，

的整数部分是3，

故答案为3．

【点睛】

本题考查了估算无理数的大小，解题的关键是熟练掌握求一个数的平方．

4、##

【分析】

根据立方根和算术平方根的求解方法求解即可．

【详解】

解：，

故答案为：．

【点睛】

本题主要考查了算术平方根和立方根，熟知二者的定义是解题的关键．

5、

【分析】

先根据数轴上点的位置求出，即可得到，由此求解即可．

【详解】

解：∵A，B，C在数轴上对应的点分别为a，﹣1， ，

∴，

∴，

∴，

∴，

故答案为：．

【点睛】

本题主要考查了实数与数轴，解题的关键在于能够根据题意求出．

三、解答题

1、（1）或；（2）9

【分析】

（1）由大正方形的边长为可得面积，由大正方形由两个小正方形与两个长方形组成，可利用面积和表示大正方形的面积，从而可得答案；

（2）由（1）可得：再把a2+b2＝57，ab＝12，利用平方根的含义解方程即可.

【详解】

解：（1） 大正方形的边长为

大正方形由两个小正方形与两个长方形组成，

（2）由（1）得：

a2+b2＝57，ab＝12，

则

【点睛】

本题考查的是完全平方公式的几何背景，利用平方根的含义解方程，掌握“完全平方公式在几何图形中的应用”是解本题的关键.

2、

（1）；

（2），证明见解析；

（3）

【分析】

（1）根据前几个等式的变化规律即可求解；

（2）根据前几个等式的变化规律即可得出第n个等式，根据异分母分式的减法法则证明即可；

（3）根据前三组观察出的变化规律求解即可．

（1）

解：∵，

∴第5个等式为；

（2）

解：∵，

∴第n个等式为，

证明：右边=，

左边=，

∵右边=左边，

∴；

（3）

解：∵=，=，=，

∴，

∴

=

=

=

=

=．

【点睛】

本题考查分式规律性问题，涉及用代数式表示数的规律、异分母分式的减法、与实数运算有关的规律题，理解题意，正确得出变化规律，会利用类比的思想方法解决问题是解答的关键．

3、（1）2＋2；（2）4

【分析】

（1）原式利用立方根性质及绝对值的代数意义化简，合并即可得到结果；

（2）原式利用乘方的意义，算术平方根定义计算即可得到结果．

【详解】

解：（1）原式＝2﹣2＋|﹣4|

＝2﹣2＋4

＝2＋2；

（2）原式＝﹣1＋5

＝4．

【点睛】

本题考查了实数的混合运算，正确的求得立方根和算术平方根是解题的关键．

4、（1）；（2）

【分析】

（1）先计算乘方运算，求解算术平方根，化简绝对值，再合并即可；

（2）提取公因式即可.

【详解】

解：（1）解：原式

（2）解：原式

【点睛】

本题考查的是立方根的含义，绝对值的化简，实数的运算，提公因式法分解因式，掌握“实数的运算及提公因式分解因式”是解本题的关键.

5、这个长方体的长、宽、高分别为、、

【分析】

根据题意设这个长方体的长、宽、高分别为4x、2x、x，然后依据底面积为24cm2，列出关于x的方程，然后可求得x的值，最后再求得这个长方体的长、宽、高即可．

【详解】

解：设这个长方体的长、宽、高分别为4x、2x、x．

根据题意得：4x•2x＝24，

解得：x＝或x＝﹣（舍去）．

则4x＝4，2x＝2．

所以这个长方体的长、宽、高分别为4cm、2cm、cm．

【点睛】

本题主要考查的是算术平方根的定义，熟练掌握算术平方根的定义是解题的关键．

6、（1）8；（2）0；（3）2；（4）

【分析】

（1）根据算术平方根的计算法则求解即可；

（2）根据算术平方根的计算法则求解即可；

（3）根据立方根的求解方法求解即可；

（4）根据求平方根的方法解方程即可．

【详解】

解：（1）

，

故答案为：8；

（2）

，

故答案为：0；

（3）∵，

∴的立方根是2，

故答案为：2；

（4）∵x2＝（﹣7）2，

∴x2＝49，

∴x=±7．

故答案为：±7．

【点睛】

本题主要考查了实数的运算，立方根，算术平方根，利用平方根解方程等等，熟知相关计算法则是解题的关键．

7、（1）；（2）.

【分析】

（1）由题意利用算术平方根和立方根的性质进行化简计算即可；

（2）由题意先去绝对值，进而进行算术平方根的加减运算即可.

【详解】

解：（1）

（2）

【点睛】

本题考查实数的运算，熟练掌握并利用算术平方根和立方根的性质进行化简是解题的关键.

8、64或﹣64

【分析】

根据平方根、立方根、有理数的乘方解决此题．

【详解】

解：∵a2＝16，b3＝27，

∴a＝±4，b＝3．

当a＝4，b＝3时，ab＝43＝64．

当a＝﹣4，b＝3时，ab＝（﹣4）3＝﹣64．

综上：ab＝64或﹣64．

【点睛】

本题主要考查立方根、平方根及有理数的乘方运算，熟练掌握立方根、平方根及有理数的乘方运算是解题的关键．

9、或

【分析】

根据平方根的定义解方程即可，平方根：如果x2=a，则x叫做a的平方根，记作“±”(a称为被开方数)

【详解】

解：（x﹣1）2 ﹣16 = 0

或

解得或

【点睛】

本题考查了根据平方根的定义解方程，掌握平方根的定义是解题的关键．

10、（1）-7；（2）x＝9．

【分析】

（1）直接利用绝对值的性质、零指数幂的性质、负整数指数幂的性质分别化简得出答案；

（2）直接去分母，移项合并同类项解方程即可．

【详解】

解：（1）原式＝﹣9﹣1+2﹣9×（﹣）

＝﹣9﹣1+2+1

＝﹣7；

（2）去分母得：2x﹣3（1+x）＝﹣12，

去括号得：2x﹣3﹣3x＝﹣12，

移项得：2x﹣3x＝﹣12+3，

合并同类项得：﹣x＝﹣9，

系数化1得：x＝9．

【点睛】

此题主要考查了实数运算以及一元一次方程的解法，正确掌握相关运算法则是解题关键．