北京课改版七年级下册第七章 观察、猜想与证明综合与测试一课一练

这是一份北京课改版七年级下册第七章 观察、猜想与证明综合与测试一课一练，共21页。试卷主要包含了下列说法不正确的是，已知，则的余角的补角是等内容，欢迎下载使用。
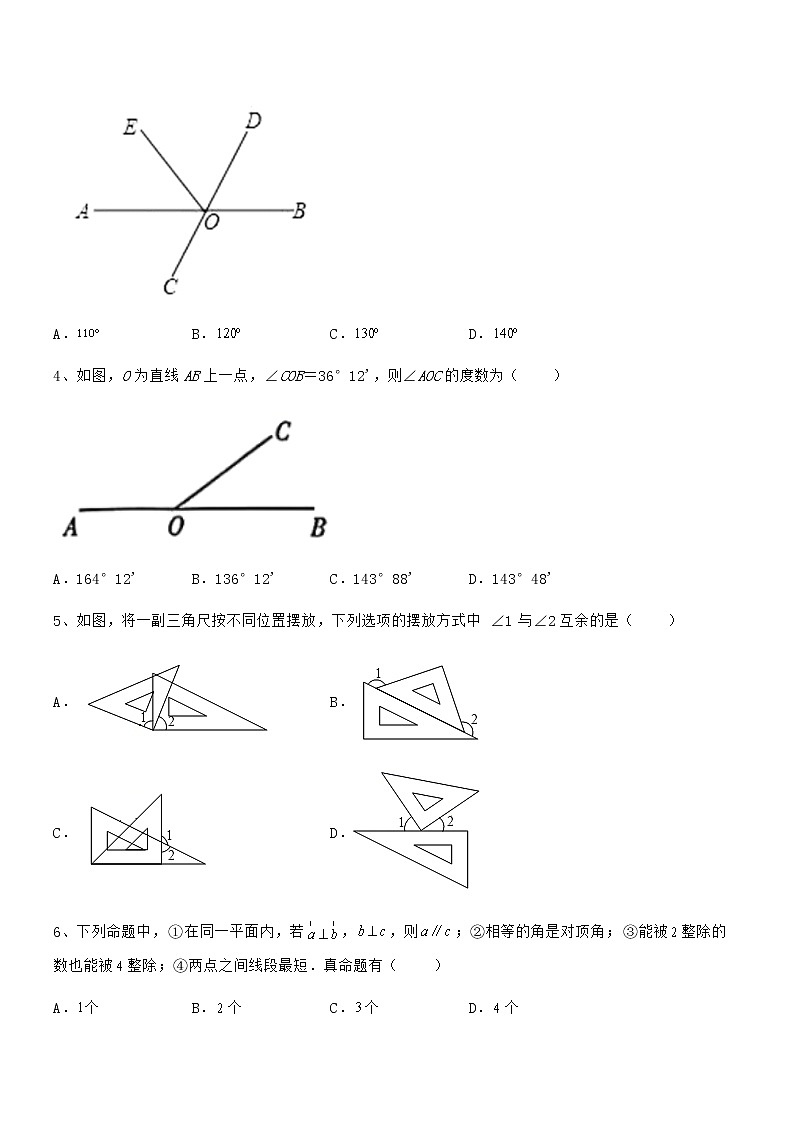
京改版七年级数学下册第七章观察、猜想与证明综合练习 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、下列说法：①和为180°且有一条公共边的两个角是邻补角；②过一点有且只有一条直线与已知直线垂直；③同位角相等；④经过直线外一点，有且只有一条直线与这条直线平行，其中正确的有（    ）A．0个 B．1个 C．2个 D．3个2、下列命题：①平面内，垂直于同一条直线的两直线平行；②经过直线外一点，有且只有一条直线与这条直线平行；③垂线段最短；④同旁内角互补．其中，正确命题的个数有（　　）A．1个 B．2个 C．3个 D．4个3、如图，已知直线，相交于O，平分，，则的度数是（    ）A． B． C． D．4、如图，O为直线AB上一点，∠COB＝36°12'，则∠AOC的度数为（　　）A．164°12' B．136°12' C．143°88' D．143°48'5、如图，将一副三角尺按不同位置摆放，下列选项的摆放方式中∠1与∠2互余的是（　　）A． B．C． D．6、下列命题中，①在同一平面内，若，，则；②相等的角是对顶角；③能被整除的数也能被整除；④两点之间线段最短．真命题有（    ）A．个 B．个 C．个 D．个7、下列说法不正确的是（　　）A．两点确定一条直线B．经过一点只能画一条直线C．射线AB和射线BA不是同一条射线D．若∠1+∠2＝90°，则∠1与∠2互余8、如图，货轮O航行过程中，同时发现灯塔A和轮船B，灯塔A在货轮O北偏东40°的方向，∠AOE＝∠BOW，则轮船B在货轮（　　）A．西北方向 B．北偏西60° C．北偏西50° D．北偏西40°9、已知，则的余角的补角是（    ）A． B． C． D．10、下列各图中，∠1与∠2是对顶角的是（　　）A． B．C． D．第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、已知一个角的补角是这个角的余角的3倍，则这个角是______度．2、_________°，的余角是________．3、已知∠1与∠2互余，若∠1=33°27′，则∠2的补角的度数是___________．4、如图，直线AB、CD相交于O，∠COE是直角，∠1＝57°，则∠2＝_____．
 5、已知∠α的余角等于68°22'，则∠α＝_____．三、解答题（5小题，每小题10分，共计50分）1、填写推理理由：   如图，CD∥EF，∠1=∠2，求证：∠3=∠ACB．证明：∵CD∥EF，∴∠DCB=∠2 ∵∠1=∠2，∴∠DCB=∠1． ∴GD∥CB ．∴∠3=∠ACB ．2、如图，直线AB与CD相交于点O，OC平分∠BOE，OF⊥CD，垂足为点O．（1）写出∠AOF的一个余角和一个补角．（2）若∠BOE＝60°，求∠AOD的度数．（3）∠AOF与∠EOF相等吗？说明理由．3、如图，，OB是的角平分线．（1）当时，求的度数．（2）的余角是多少度？4、已知，与互余，OP是的角平分线．（1）画出所有符合条件的图形．（2）计算的度数．5、已知AB∥CD，点是AB，CD之间的一点．（1）如图1，试探索∠AEC，∠BAE，∠DCE之间的数量关系；以下是小明同学的探索过程，请你结合图形仔细阅读，并完成填空（理由或数学式）：解：过点E作PE∥AB（过直线外一点有且只有一条直线与这条直线平行）．∵AB∥CD（已知），∴PE∥CD（ 　   　），∴∠BAE＝∠1，∠DCE＝∠2（ 　   　），∴∠BAE+∠DCE＝　   　+　   　（等式的性质）．即∠AEC，∠BAE，∠DCE之间的数量关系是 　   　．（2）如图2，点F是AB，CD之间的一点，AF平分∠BAE，CF平分∠DCE．①若∠AEC＝74°，求∠AFC的大小；②若CG⊥AF，垂足为点G，CE平分∠DCG，∠AEC+∠AFC＝126°，求∠BAE的大小． ---------参考答案-----------一、单选题1、B【分析】根据举反例可判断①，根据垂线的定义可判断②，根据举反例可判断③，根据平行线的基本事实可判断④．【详解】解：①如图∠AOC=∠2=150°，∠BOC=∠1=30°，满足∠1+∠2=180°，射线OC是两角的共用边，但∠1与∠2不是邻补角，故①不正确；②在同一个面内，过一点有且只有一条直线与已知直线垂直，故②不正确；③如图直线a、b被直线c所截，∠1与∠2是同位角，但∠1＞∠2，故③不正确； ④经过直线外一点，有且只有一条直线与这条直线平行，是基本事实，故④正确；其中正确的有④一共1个．故选择B．【点睛】本题考查基本概念的理解，掌握基本概念是解题关键．2、C【分析】根据平行线的性质与判定可以判断①②④，根据垂线段最短可以判断③．【详解】解：①平面内，垂直于同一条直线的两直线平行，是真命题；②经过直线外一点，有且只有一条直线与这条直线平行，是真命题；③垂线段最短，是真命题；④两直线平行，同旁内角互补，是假命题，∴真命题有3个，故选C．【点睛】本题主要考查了判断命题真假，熟知相关知识是解题的关键．3、C【分析】先根据角平分线的定义求得∠AOC的度数，再根据邻补角求得∠BOC的度数即可．【详解】解：∵OA平分∠EOC，∠EOC＝100°，∴∠AOC＝∠EOC＝50°，∴∠BOC＝180°﹣∠AOC＝130°．故选：C．【点睛】本题考查角平分线的有关计算，邻补角．能正确识图是解题关键．4、D【分析】根据邻补角及角度的运算可直接进行求解．【详解】解：由图可知：∠AOC+∠BOC=180°，∵∠COB＝36°12'，∴∠AOC=180°-∠BOC=143°48'，故选D．【点睛】本题主要考查邻补角及角度的运算，熟练掌握邻补角及角度的运算是解题的关键．5、D【分析】由题意直接根据三角板的几何特征以及余角的定义进行分析计算判断即可．【详解】解：A．∵∠1+∠2度数不确定，
∴∠1与∠2不互为余角，故错误；
B．∵∠1+45°+∠2+45°=180°+180°=360°，
∴∠1+∠2=270°，
即∠1与∠2不互为余角，故错误；
C．∵∠1+∠2=180°，
∴∠1与∠2不互为余角，故错误；
D．∵∠1+∠2+90°=180°，
∴∠1+∠2=90°，
即∠1与∠2互为余角，故正确．
故选：D．【点睛】本题主要考查余角和补角，熟练掌握余角的定义即若两个角的和为90°，则这两个角互为余角是解题的关键．6、B【分析】根据对顶角的定义以及数的整除性和两点之间线段最短分析得出即可．【详解】解：①在同一平面内，若a⊥b，b⊥c，则a∥c，故为真命题；②相等的角不一定是对顶角，故为假命题；③能被2整除的数不一定能被4整除，故为假命题；④两点之间线段最短，故为真命题；故选B．【点睛】此题主要考查了命题与定理，熟练掌握相关的定理是解题关键．7、B【分析】根据两点确定一条直线，即可判断A；根据过一点可以画无数条直线可以判断B；根据射线的表示方法即可判断C；根据余角的定义，可以判断D．【详解】解：A、两点确定一条直线，说法正确，不符合题意；B、过一点可以画无数条直线，说法错误，符合题意；C、射线AB和射线BA不是同一条射线，说法正确，不符合题意；D、若∠1+∠2＝90°，则∠1与∠2互余，说法正确，不符合题意；故选B．【点睛】本题主要考查了两点确定一条直线，；过一点可以画无数条直线，射线的表示方法余角的定义，熟知相关知识是解题的关键．8、D【分析】根据题意得：∠AON=40°，再由等角的余角相等，可得∠BON=∠AON=40°，即可求解．【详解】解：根据题意得：∠AON=40°，∵∠AOE＝∠BOW，∠AON+∠AOE=90°，∠BON+∠BOW=90°，∴∠BON=∠AON=40°，∴轮船B在货轮的北偏西40°方向．故选：D【点睛】本题主要考查了余角的性质，方位角，熟练掌握等角的余角相等是解题的关键．9、A【分析】根据余角和补角定义解答．【详解】解：的余角的补角是，故选：A ．【点睛】此题考查余角和补角的定义：和为90度的两个角互为余角，和为180度的两个角是互为补角．10、B【分析】根据对顶角的定义作出判断即可．【详解】解：根据对顶角的定义可知：只有B选项的是对顶角，其它都不是．故选：B．【点睛】本题考查对顶角的定义，解题关键是明确两条直线相交后所得的只有一个公共顶点且两边互为反向延长线，这样的两个角叫做对顶角．二、填空题1、【分析】设这个角为 则这个角的补角为： 这个角的余角为： 根据等量关系一个角的补角是这个角的余角的3倍，列方程，解方程可得．【详解】解：设这个角为 则这个角的补角为： 这个角的余角为： ， ，，， 答：这个角为．故答案为：．【点睛】本题考查的是余角与补角的含义，一元一次方程的应用，掌握以上知识是解题的关键．2、        【分析】根据角度的四则运算法则、余角的定义即可得．【详解】解：，，，，，；的余角是，故答案为：，．【点睛】本题考查了角度的四则运算、余角，熟练掌握角度的四则运算法则和余角的定义是解题关键．3、123°27′【分析】本题考查互补和互余的概念，和为180度的两个角互为补角；和为90度的两个角互为余角．【详解】解：∠1与∠2互余，且∠1=∠1=33°27′，则∠2=90°-33°27′=56°33′，∠2的补角的度数为180°-56°33′=123°27′．故答案为：123°27′．【点睛】本题考查的是余角和补角的概念，如果两个角的和等于90°，就说这两个角互为余角；如果两个角的和等于180°，就说这两个角互为补角．4、33°【分析】由题意直接根据∠2＝180°﹣∠COE﹣∠1，进行计算即可得出答案．【详解】解：由题意得：∠2＝180°﹣∠COE﹣∠1＝180°﹣90°﹣57°＝33°．故答案为：33°．【点睛】本题考查余角和补角的知识，属于基础题，注意数形结合思维分析的运用．5、【分析】根据余角的概念（如果两个角的和为，那么称这两个角“互为余角”）即可解答．【详解】解：由余角的定义得：，故答案为：．【点睛】本题考查余角的定义、角度的计算，熟记互为余角的两个角的和为90°是解答的关键．三、解答题1、两直线平行，同位角相等；等量代换；内错角相等，两直线平行；两直线平行，同位角相等．【解析】【分析】根据两直线平行，同位角相等可以求出∠DCB=∠2，等量代换得出∠DCB=∠1，再根据内错角相等，两直线平行得出GD∥CB，最后根据两直线平行，同位角相等，所以∠3=∠ACB．【详解】证明：∵CD∥EF，  ∴∠DCB=∠2（两直线平行，同位角相等），∵∠1=∠2，∴∠DCB=∠1（等量代换）． ∴GD∥CB（内错角相等，两直线平行）．∴∠3=∠ACB（两直线平行，同位角相等）．故答案为：两直线平行，同位角相等；等量代换；内错角相等，两直线平行；两直线平行，同位角相等．【点睛】本题考查了平行线的判定与性质，熟练掌握平行线的判定方法和性质，并准确识图是解题的关键．2、（1）∠AOF的余角是：∠COE或∠BOC或∠AOD；∠AOF的补角是∠BOF；（2）30°；（3）∠AOF=∠EOF，理由见解析【解析】【分析】（1）由OC⊥CD，可得∠DOF=90°，则∠AOF+∠AOD=90°，由对顶角相等得∠BOC=∠AOD，则∠AOF+∠BOC=90°，由OC平分∠BOE，可得∠COE=∠BOC，∠AOF+∠COE=90°；由∠AOF+∠BOF=180°，可得∠AOF的补角是∠BOF；（2）由OC平分∠BOE，∠BOE=60°，可得∠BOC=30°，再由∠AOD=∠BOC，即可得到∠AOD=30°；（3）由（1）可得∠AOD=∠BOC=∠COE，再由OF⊥OC，得到∠DOF=∠COF=90°，则∠AOD+∠AOF=∠EOF+∠COE=90°，即可推出∠AOF=∠EOF．【详解】解：（1）∵OC⊥CD，∴∠DOF=90°，∴∠AOF+∠AOD=90°，又∵∠BOC=∠AOD，∴∠AOF+∠BOC=90°，∵OC平分∠BOE，∴∠COE=∠BOC，∴∠AOF+∠COE=90°；∴∠AOF的余角是，∠COE，∠BOC，∠AOD；∵∠AOF+∠BOF=180°，∴∠AOF的补角是∠BOF；（2）∵OC平分∠BOE，∠BOE=60°，∴∠BOC=30°，又∵∠AOD=∠BOC，∴∠AOD=30°；（3）∠AOF=∠EOF，理由如下：由（1）可得∠AOD=∠BOC=∠COE，∵OF⊥OC，∴∠DOF=∠COF=90°，∴∠AOD+∠AOF=∠EOF+∠COE=90°，∴∠AOF=∠EOF．【点睛】本题主要考查了与余角、补角有关的计算，等角的余角相等，垂线的定义，解题的关键在于熟知余角与补角的定义：如果两个角的相加的度数为90度，那么这两个角互余，如果两个角相加的度数为180度，那么这两个角互补．3、（1）的度数．（2）的余角是．【解析】【分析】（1）利用角平分线的性质，求得的度数，然后利用，即可求解的度数．（2）利用题（1）中的度数以及余角的概念，直接求解即可．【详解】（1）解： OB是的角平分线．，，，，．（2）解：由（1）得，故的余角．【点睛】本题主要是考查了角平分线以及余角的相关概念及性质和角的计算，熟练利用角平分线的性质求解角度，找到所要求的角与已知角的关系，是解决该题的关键．4、（1）见解析；（2）15°或45°【解析】【分析】（1）分当OC在外部时和当OC在内部时，两种情况，分别作图即可；（2）根据（1）所求和角平分线，余角的定义求解即可．【详解】解：（1）如图所示，即为所求；（2）当OC在外部时（如图1），∵，与互余，∴，∴，∴OP是的角平分线，∴，∴当OC在内部时（如图2）∵，与互余∴，∴∴OP是的角平分线∴∴综上：或45°．【点睛】本题主要考查了角平分线的定义，余角的定义，熟知角平分线和余角的定义是解题的关键．5、（1）平行于同一条直线的两条直线平行，两直线平行，内错角相等，∠1，∠2，∠AEC＝∠BAE+∠DCE；（2）①37°；②52°【解析】【分析】（1）结合图形利用平行线的性质填空即可；（2）①过F作FG∥AB，由（1）得：∠AEC＝∠BAE+∠DCE，根据AB∥CD，FG∥AB，CD∥FG，得出∠AFC=∠AFG+∠GFC＝∠BAF+∠DCF，根据AF平分∠BAE，CF平分∠DCE，可得∠BAF＝∠BAE，∠DCF＝∠DCE，根据角的和差∠AFC＝∠BAF+∠DCF=∠AEC即可；②由①得：∠AEC＝2∠AFC，可求∠AFC＝42°，∠AEC＝82°，根据CG⊥AF，求出∠GCF=90-∠AFC=48°，根据角平分线计算得出∠GCF＝3∠DCF，求出∠DCF＝16°即可．【详解】解：（1）平行于同一条直线的两条直线平行，两直线平行，内错角相等，∠1，∠2，∠AEC＝∠BAE+∠DCE，故答案为：平行于同一条直线的两条直线平行，两直线平行，内错角相等，∠1，∠2，∠AEC＝∠BAE+∠DCE，（2）①过F作FG∥AB，由（1）得：∠AEC＝∠BAE+∠DCE，∵AB∥CD，FG∥AB，∴CD∥FG，∴∠BAF=∠AFG，∠DCF=∠GFC，∴∠AFC=∠AFG+∠GFC＝∠BAF+∠DCF，∵AF平分∠BAE，CF平分∠DCE，∴∠BAF＝∠BAE，∠DCF＝∠DCE，∴∠AFC＝∠BAF+∠DCF，＝∠BAE+∠DCE，=（∠BAE+∠DCE），＝∠AEC，＝×74°，＝37°；②由①得：∠AEC＝2∠AFC，∵∠AEC+∠AFC＝126°，∴2∠AFC+∠AFC＝126°∴3∠AFC＝126°，∴∠AFC＝42°，∠AEC＝84°，∵CG⊥AF，∴∠CGF＝90°，∴∠GCF=90-∠AFC=48°， ∵CE平分∠DCG，∴∠GCE＝∠ECD，∵CF平分∠DCE，∴∠DCE＝2∠DCF＝2∠ECF，∴∠GCF＝3∠DCF，∴∠DCF＝16°，∴∠DCE＝32°，∴∠BAE＝∠AEC﹣∠DCE＝52°．【点睛】本题考查平行线性质，角平分线有关的计算，垂直定义，角的和差倍分，简单一元一次方程，掌握平行线性质，角平分线有关的计算，垂直定义，角的和差倍分，简单一元一次方程是解题关键．