初中数学人教版七年级下册第五章 相交线与平行线综合与测试复习练习题

这是一份初中数学人教版七年级下册第五章 相交线与平行线综合与测试复习练习题，文件包含第10讲相交线与平行线章节测试题B卷-七年级数学下册知识点同步练习人教版解析版docx、第10讲相交线与平行线章节测试题B卷-七年级数学下册知识点同步练习人教版原卷版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。

人教版数学七年级下册
第5章相交线与平行线章节测试B卷
考试时间：120分钟 满分：120分

姓名：__________ 班级：__________考号：__________

题号
一
二
三
总分
评分
 
 
 
 
一、选择题（共10题；共30分）
1.下列图形中,哪个可以通过图1平移得到（   ）

A.                         B.                         C.                         D. 
【答案】 A
【考点】图形的平移
【解析】【解答】因为图形平移前后，不改变图形的形状和大小，只是位置发生改变，所以由图1平移可得A，
故答案为：A．
【分析】平移只改变图形的位置，不改变图形的形状和大小，据此判断即可.
2.如图所示，在10×6的网格中，每个小方格的边长都是1个单位，将△ABC平移到△DEF的位置，下面正确的平移步骤是（    ）

A. 先向左平移5个单位，再向下平移2个单位
B. 先向右平移5个单位，再向下平移2个单位
C. 先向左平移5个单位，再向上平移2个单位
D. 先向右平移5个单位，再向上平移2个单位
【答案】A
【考点】平移的性质
【解析】【解答】平移步骤是：先把△ABC向左平移5个单位，再向下平移2个单位，故答案为：A．
【分析】根据网格结构，观察对应点A、D，点A向左平移5个单位，再向下平移2个单位即可到 达点 D的位置 ，根据平移性质即可得出平移步骤。
3.如图，在下列四组条件中，能判定AB∥CD的是(    )

A. ∠1=∠2                    B. ∠ABD=∠BDC                    C. ∠3=∠4                    D. ∠BAD+∠ABC=180°
【答案】 B
【考点】平行线的判定
【解析】【解答】A.因为∠1=∠2，而且∠1与∠2是内错角，则AD//BC，不符合；
B.因为∠ABD=∠BDC，而且∠ABD与∠BDC是内错角，则AB//CD，符合；
C.因为∠3=∠4，而且∠3与∠4是内错角，则AD//BC，不符合；
D.因为∠BAD+∠ABC=180°，而且∠BAD与∠ABC是同旁内角，则AD//BC，不符合；
【分析】根据平行线的判定理去判断：（1）同位角相等，两直线平行；（2）内错角相等， 两直线平行；（3）同旁内角互补，两直线平行.
4.下列图形中,线段AD的长表示点A到直线BC距离的是(   )
A.       B .  C.                    D. 
【答案】D
【考点】点到直线的距离
【解析】【解答】解：∵线段AD的长表示点A到直线BC距离
∴过点A作BC的垂线，
A、过点A作DA⊥AB，故A不符合题意；
B、AD与BC相交，故B不符合题意；
C、过点A作DA⊥AB，故C不符合题意；
D、过点A作AD⊥BC，交BC的延长线于点D，故D符合题意；
故答案为：D
【分析】根据已知条件线段AD的长表示点A到直线BC距离，因此应该过点A作BC的垂线，观察图形即可得出答案。
5.如图，已知AB∥CD，BC平分∠ABE，∠C=33°，则∠CEF的度数是（   ）

A. 16°                                       B. 33°                                       C. 49°                                       D. 66°
【答案】D
【考点】平行线的性质
【解析】【解答】解：∵AB∥CD，∠C=33°，
∴∠ABC=∠C=33°．
∵BC平分∠ABE，
∴∠ABE=2∠ABC=66°，
∴∠CEF=∠ABE=66°．
故答案为：D
【分析】由两直线平行，内错角相等，可求出∠ABC的度数，再用角平分线的性质可求出∠ABE的度数，即可求出∠CEF的度数.
6.如图,如果AB∥CD,CD∥EF,那么∠BCE等于(    )

A. ∠1+∠2          B. ∠2-∠1          C. 180°-∠2+∠1          D. 180°-∠1+∠2
【答案】C
【考点】平行线的性质
【解析】【解答】解：∵B∥CD
∴∠1=∠BCD
∵CD∥EF,
∴∠2+∠DCE=180°
∠DCE=180°-∠2
∵∠BCE=∠BCD+ ∠DCE
∴∠BCE=180°-∠2+∠1
故答案为：C
【分析】根据两直线平行内错角相等即同旁内角互补，可得出∠1=∠BCD，∠2+∠DCE=180°，再根据∠BCE=∠BCD+ ∠DCE，即可得出结论。
7.如果直线MN外一点A到直线MN的距离是2 cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定(   )
A. 等于2 cm                      B. 小于2 cm                      C. 大于2 cm                      D. 大于或等于2 cm
【答案】D
【考点】垂线段最短
【解析】【解答】解：根据“在连接直线外一点与直线上各点的线段中,垂线段最短”,
可知2 cm是连接点A与直线MN上各点的线段中最短线段的长度
故答案为：D
【分析】根据垂线段最短，可得出答案。
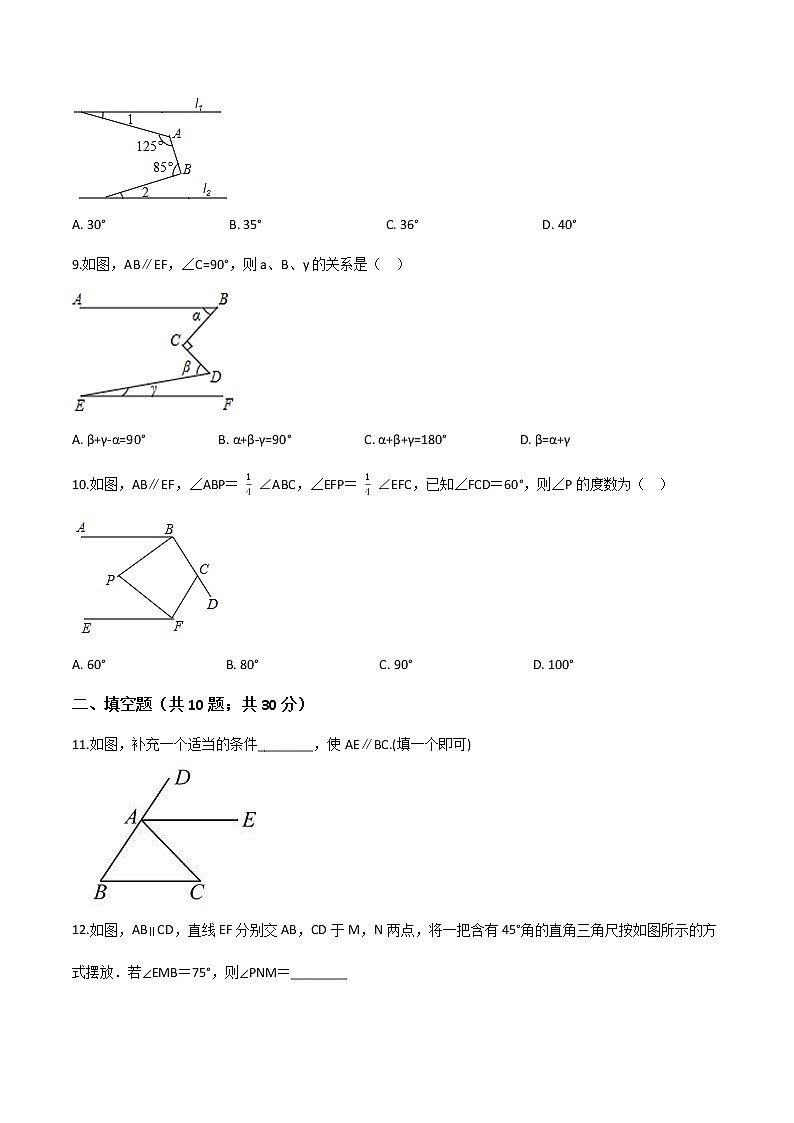
8.如图，直线l1∥l2 ， ∠A=125°，∠B=85°，则∠1+∠2=（   ）

A. 30°                                       B. 35°                                       C. 36°                                       D. 40°
【答案】A
【考点】平行线的性质
【解析】【解答】解：如图，过点A作l1的平行线，过点B作l2的平行线，
∴∠3=∠1，∠4=∠2，
∵l1∥l2 ，
∴AC∥BD，
∴∠CAB+∠ABD=180°，
∴∠3+∠4=125°+85°﹣180°=30°，
∴∠1+∠2=30°．
故选：A．

【分析】过点A作l1的平行线，过点B作l2的平行线，根据两直线平行，内错角相等可得∠3=∠1，∠4=∠2，再根据两直线平行，同旁内角互补求出∠CAB+∠ABD=180°，然后计算即可得解．
9.如图，AB∥EF，∠C=90°，则a、B、y的关系是（   ）

A. β+γ-α=90°                       B. α+β-γ=90°                       C. α+β+γ=180°                       D. β=α+γ
【答案】 B
【考点】平行线的性质
【解析】【解答】如图，分别过点C、D作AB的平行线，

根据平行线的性质得 α+β−γ=90° .故答案为：B.
【分析】如图，分别过点C、D作AB的平行线，根据两直线平行内错角相等，可得a=∠1，∠2=∠3，∠4=γ，由β=∠3+∠4，继而可得a、β、γ的关系.
10.如图，AB∥EF，∠ABP＝ 14 ∠ABC，∠EFP＝ 14 ∠EFC，已知∠FCD＝60°，则∠P的度数为（   ）

A. 60°                                      B. 80°                                      C. 90°                                      D. 100°
【答案】 A
【考点】平行公理及推论，平行线的性质
【解析】【解答】解：过C作CQ∥AB，

∵AB∥EF，
∴AB∥EF∥CQ，
∴∠ABC＋∠BCQ＝180°，∠EFC＋∠FCQ＝180°，
∴∠ABC＋∠BCF＋∠EFC＝360°，
∵∠FCD＝60°，
∴∠BCF＝120°，
∴∠ABC＋∠EFC＝360°﹣120°＝240°，
∵∠ABP＝ 14 ∠ABC，∠EFP＝ 14 ∠EFC，
∴∠ABP＋∠PFE＝60°，
∴∠P＝60°.
故答案为：A.
【分析】过C作CQ∥AB，利用平行线的判定与性质进行解答即可.
二、填空题（共10题；共30分）
11.如图，补充一个适当的条件________，使AE∥BC.(填一个即可)

【答案】 ∠B=∠DAE 或 (∠C=∠CAE)
【考点】平行线的判定
【解析】【解答】解：若∠B=∠DAE可根据同位角相等，两直线平行得到AE∥BC；
若∠C=∠CAE可根据内错角相等，两直线平行得到AE∥BC；
故答案为： ∠B=∠DAE 或 (∠C=∠CAE) （答案不唯一）
【分析】根据平行线的判定方法：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行进行分析即可.
12.如图，AB∥CD，直线EF分别交AB，CD于M，N两点，将一把含有45°角的直角三角尺按如图所示的方式摆放．若∠EMB＝75°，则∠PNM＝________

【答案】 30°
【考点】平行线的性质
【解析】【解答】解：∵ AB∥CD ， ∠EMB＝75°，
∴∠MND= ∠EMB＝75°，
∴ ∠PNM =∠MND-∠PND=75°-45°=30°；
故答案为：30°。
【分析】根据二直线平行，同位角相等得出∠MND= ∠EMB＝75°，再根据角的和差，由 ∠PNM =∠MND-∠PND即可算出答案。
13.如图，AB∥CD,直线EF分别交AB、CD于点E、F，EG平分∠AEF，∠1=35º，那么∠2=________度.

【答案】110
【考点】平行线的性质
【解析】【解答】解：∵AB∥CD，
∴∠AEG=∠1=35°，
∵EG平分∠AEF，
∴∠AEF=2∠AEG=2×35°=70°，
∴∠2=180°-∠AEF=180°-70°=110°．
故答案为：110．
【分析】根据两直线平行，内错角相等可得∠AEG=∠1，再根据角平分线的定义求出∠AEF，然后根据邻补角的定义列式计算即可得解．
14.如图，边长为4cm的正方形ABCD先向上平移2cm，再向右平移1cm，得到正方形A′B′C′D′，此时阴影部分的面积为________cm2 ．

【答案】6
【考点】平移的性质
【解析】【解答】解：∵边长为4cm的正方形ABCD先向上平移2cm，
∴阴影部分的宽为4﹣2=2cm，
∵向右平移1cm，
∴阴影部分的长为4﹣1=3cm，
∴阴影部分的面积为3×2=6cm2 ．
故答案为：6．
【分析】先依据平移的方向和距离确定阴影部分的长和宽，然后依据矩形的面积=长×宽求解即可.
15.如图：直线l1∥l2 ， 一块含30°角的直角三角板如图所示放置，∠1=25°，则∠2=________.

【答案】 35°
【考点】平行线的性质
【解析】【解答】解：如图，过点M作MN∥ l1 ，

∴MN∥ l1∥ l2，
∵ l1∥ MN，
∴∠2=∠4，
∵ l2∥MN，
∴∠3=∠5，
∵∠1=∠5，
∴∠3=∠1，
∴∠1+∠2=∠3+∠4=60°，
∴∠2=60°-∠1=60°-25°=35°.
【分析】过点M作MN∥ l1 ，则MN∥ l1∥ l2， 分别由 l1∥ MN，  l2∥MN， 可得∠2和∠4相等，∠3和∠5相等，结合对顶角相等，则∠1与∠2之和转化为∠3与∠4之和，再结合三角板这个内角为60°，即可求得∠2的大小.
16.如图，△ABC中，∠B＝90°，AB＝6，BC＝8，将△ABC平移至△DEF的位置，若CF＝3，DG＝2，则阴影部分面积为________.

【答案】 14
【考点】平移的性质
【解析】【解答】解：∵将△ABC平移至△DEF的位置
∴DE=AB=6,EF=BC=8
∴CE=EF-CF=5,GE=DE-DG=4
∴阴影部分的面积为: 12 ×6×8- 12 ×5×4=14.
【分析】先根据平移的性质得到DE=AB=6,EF=BC=8,然后再运用线段的和差求得GE和CE,最后运用阴影部分的面积=三角形DEF的面积-三角形GEC的面积即可.
17.如图a是长方形纸带，∠DEF=25°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是________°．

【答案】 105
【考点】平行线的性质
【解析】【解答】解：∵AD∥BC，∠DEF=25°，
∴∠BFE=∠DEF=25°，
∴∠EFC=155°（图a），
∴∠BFC=155°﹣25°=130°（图b），
∴∠CFE=130°﹣25°=105°（图c）．
故答案为：105．
【分析】根据两条直线平行，内错角相等，则∠BFE=∠DEF=25°，根据平角定义，则∠EFC=155°（图a），进一步求得∠BFC=155°﹣25°=130°（图b），进而求得∠CFE=130°﹣25°=105°（图c）．
18.如图，EF∥AD，∠1=∠2，∠BAC=70°.将求∠AGD的过程填写完整.

∵EF∥AD，（________）
∴∠2=________.（两直线平行，同位角相等；）
又∵∠1=∠2，（________）
∴∠1=∠3.（________）
∴AB∥DG.（________）
∴∠BAC+________=180°（________）
又∵∠BAC=70°，（________）
∴∠AGD=________.
【答案】 已知；∠3；已知；等量代换；内错角相等，两直线平行；∠AGD；两直线平行，同旁内角互补；已知；110°.
【考点】平行线的判定与性质
【解析】解：∵EF∥AD，（已知）
∴∠2=∠3.（两直线平行，同位角相等；）
又∵∠1=∠2，（已知）
∴∠1=∠3.（等量代换）
∴AB∥DG.（内错角相等，两直线平行）
∴∠BAC+∠AGD=180°（两直线平行，同旁内角互补）
又∵∠BAC=70°，（已知）
∴∠AGD=110°.
【分析】根据平行线的判定定理及性质性质即可一一填出答案.
19.如图，已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=100°，则∠DBA的度数为________．

【答案】50°
【考点】平行线的性质
【解析】【解答】解：

如图，设∠DAB=∠BAC=x，即∠1=∠2=x，
∵EF∥GH，
∴∠2=∠3，
在△ABC内，∠4=180°﹣∠ACB﹣∠1﹣∠3=180°﹣∠ACB﹣2x，
∵直线BD平分∠FBC，
∴∠5= 12 （180°﹣∠4）= 12 （180°﹣180°+∠ACB+2x）= 12 ∠ACB+x，
∴∠DBA=180°﹣∠3﹣∠4﹣∠5
=180°﹣x﹣（180°﹣∠ACB﹣2x）﹣（ 12 ∠ACB+x）
=180°﹣x﹣180°+∠ACB+2x﹣ 12 ∠ACB﹣x
= 12 ∠ACB
= 12 ×100°
=50°．
故答案为：50°．
【分析】根据两直线平行，内错角相等可得∠2=∠3，再根据三角形的内角和定理表示出∠4，然后表示∠5，再利用平角等于180°列式表示出∠DBA整理即可得解．
20.如图，将一副直角三角板放在同一条直线AB上，其中∠ONM=30°，∠OCD=45°．将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周，在旋转的过程中，当第________秒时，直线CD恰好与直线MN垂直．

【答案】5.5或11.5
【考点】垂线
【解析】【解答】解：如图，CD在OM的右边时，设CD与AB相交于G， ∵CD⊥MN，
∴∠NGC=90°﹣∠MNO=90°﹣30°=60°，
∴∠CON=∠NGC﹣∠OCD=60°﹣45°=15°，
∴旋转角为180°﹣∠CON=180°﹣15°=165°，
t=165°÷30°=5.5秒，
CD在OM的左边时，设CD与AB相交于G，
∵CD⊥MN，
∴∠NGD=90°﹣∠MNO=90°﹣30°=60°，
∴∠AOC=∠NGD﹣∠C=60°﹣45°=15°，
∴旋转角为360°﹣∠AOC=360°﹣15°=345°，
t=345°÷30°=11.5秒，
综上所述，第5.5或11.5秒时，直线CD恰好与直线MN垂直．
故答案为：5.5或11.5．

【分析】分CD在OM的右边时，设CD与AB相交于G，根据直角三角形两锐角互余求出∠CGN，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CON，再求出旋转角即可，CD在OM的左边时，设CD与AB相交于G，根据直角三角形两锐角互余求出∠NGD，再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠AOC，然后求出旋转角，计算即可得解．
三、解答题（共5题；共60分）
21.如图，在一块长为20m，宽为14m的草地上有一条宽为2m的曲折小路，你能运用你学的知识求出这块草地的绿地面积吗？

【答案】 【解答】平移使路变直，路是长20+(14-2)m,宽2m的矩形，绿地的面积20×14－[20+(14-2)]×2＝216（m2），答：这块草地的绿地面积是216m2 ．
【考点】生活中的平移现象
【解析】【分析】根据平移，可得路是矩形，根据面积的和差，可得答案．
22.如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=120°，∠ACF=20°，求∠FEC的度数．

【答案】解：∵EF∥AD，AD∥BC， ∴EF∥BC，
∴∠ACB+∠DAC=180°，
∵∠DAC=120°，
∴∠ACB=60°，
又∵∠ACF=20°，
∴∠FCB=∠ACB﹣∠ACF=40°，
∵CE平分∠BCF，
∴∠BCE=20°，
∵EF∥BC，
∴∠FEC=∠ECB，
∴∠FEC=20°．
【考点】平行线的判定与性质
【解析】【分析】推出EF∥BC，根据平行线性质求出∠ACB，求出∠FCB，根据角平分线求出∠ECB，根据平行线的性质推出∠FEC=∠ECB，代入即可．
23.如图，∠ 1+∠ 2=180°，∠ 3=∠ B．

（Ⅰ）求证：AB∥ EF；
（Ⅱ）试判断DE与BC的位置关系，并证明你的结论．
【答案】证明：（Ⅰ）∵∠1+∠2=180°，∠1+∠DFE=180°， ∴∠DFE=∠2，
∴EF∥AB；
（Ⅱ）DE∥BC，
理由如下：
由（1）知EF∥AB，
∴∠3=∠ADE．
又∠3=∠B，
∴∠ADE=∠B，
∴DE∥BC，
∴∠AED=∠C，
∴DE∥BC．
【考点】平行线的判定与性质
【解析】【分析】（1）要证明∠AED=∠C，则需证明DE∥BC．根据等角的补角相等，得∠DFE=∠2，根据内错角相等，得直线EF∥AB；（2）由EF∥AB，得到∠3=∠ADE，从而∠ADE=∠B，即可证明结论．
24.如图，已知：CD⊥AB于点D，EF⊥AB于点F，∠1=∠2． 求证：DG∥BC．

【答案】证明：∵CD⊥AB，EF⊥AB， ∴∠CDF+∠EFD=180°，
∴CD∥EF，
∴∠2=∠DCE，
又∵∠1=∠2，
∴∠1=∠DCE，
∴DG∥BC．
【考点】垂线，平行线的判定
【解析】【分析】由垂直可证明CD∥EF，结合条件可得到∠1=∠DCE，可证明DG∥BC．
25.如图1，已知直线PQ∥ MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC=50°，∠ADC=30°，AE平分∠ PAD，CE平分∠ ACD，AE与CE相交于E．

（1）求∠AEC的度数；
（2）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1 ， CE平分∠ACD1 ， A1E与CE相交于E，∠PAC=50°，∠A1D1C=30°，求∠A1EC的度数．

（3）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（2）相同，求此时∠A1EC的度数．

【答案】 （1）解：如图1所示：
∵直线PQ∥MN，∠ADC=30°，
∴∠ADC=∠QAD=30°，
∴∠PAD=150°，
∵∠PAC=50°，AE平分∠PAD，
∴∠PAE=75°，
∴∠CAE=25°，
可得∠PAC=∠ACN=50°，
∵CE平分∠ACD，
∴∠ECA=25°，
∴∠AEC=180°﹣25°﹣25°=130°；

（2）解：如图2所示：
∵∠A1D1C=30°，线段AD沿MN向右平移到A1D1 ， PQ∥MN，
∴∠QA1D1=30°，
∴∠PA1D1=150°，
∵A1E平分∠AA1D1 ，
∴∠PA1E=∠EA1D1=75°，
∵∠PAC=50°，PQ∥MN，
∴∠CAQ=130°，∠ACN=50°，
∵CE平分∠ACD1 ，
∴∠ACE=25°，
∴∠CEA1=360°﹣25°﹣130°﹣75°=130°；

（3）解：如图3所示：过点E作FE∥PQ，

∵∠A1D1C=30°，线段AD沿MN向左平移到A1D1 ， PQ∥MN，
∴∠QA1D1=30°，
∵A1E平分∠AA1D1 ，
∴∠QA1E=∠2=15°，
∵∠PAC=50°，PQ∥MN，
∴∠ACN=50°，
∵CE平分∠ACD1 ，
∴∠ACE=∠ECN=∠1=25°，
∴∠CEA1=∠1+∠2=15°+25°=40°
【考点】平行线的性质，平移的性质
【解析】【分析】（1）直接利用角平分线的性质结合平行线的性质得出∠CAE以及∠ECA的度数，进而得出答案；（2）直接利用角平分线的性质结合平行线的性质得出∠CAE以及∠ECA的度数，进而得出答案；（3）直接利用角平分线的性质结合平行线的性质得出∠1和∠2的度数，进而得出答案．