初中数学沪科版九年级下册第24章 圆综合与测试课时作业

这是一份初中数学沪科版九年级下册第24章 圆综合与测试课时作业，共25页。试卷主要包含了点P关于原点O的对称点的坐标是等内容，欢迎下载使用。
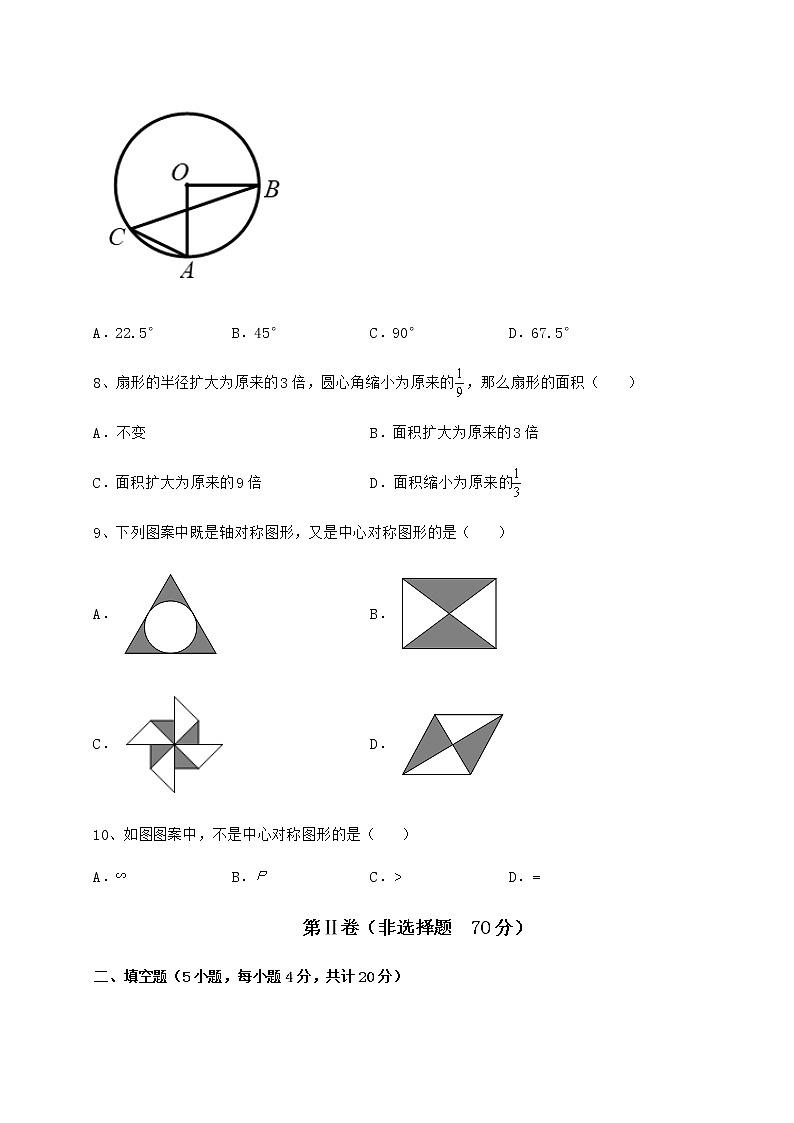
沪科版九年级数学下册第24章圆定向测评 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，在△ABC中，∠BAC＝130°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，则∠BAD的大小是（　　）A．80° B．70° C．60° D．50°2、如图，△ABC内接于⊙O，∠BAC＝30°，BC＝6，则⊙O的直径等于（　　）A．10 B．6 C．6 D．123、计算半径为1，圆心角为的扇形面积为（    ）A． B． C． D．4、点P(3，﹣2)关于原点O的对称点的坐标是（　　）A．(3，﹣2) B．(﹣3，2) C．(﹣3，﹣2) D．(2，3)5、如图，在中，，，将绕点A顺时针旋转60°得到，此时点B的对应点D恰好落在BC边上，则CD的长为（    ）A．1 B．2 C．3 D．46、如图，边长为5的等边三角形中，M是高所在直线上的一个动点，连接，将线段绕点B逆时针旋转得到，连接．则在点M运动过程中，线段长度的最小值是（    ）A． B．1 C．2 D．7、如图，点A，B，C均在⊙O上，连接OA，OB，AC，BC，如果OA⊥OB，那么∠C的度数为（    ）A．22.5° B．45° C．90° D．67.5°8、扇形的半径扩大为原来的3倍，圆心角缩小为原来的，那么扇形的面积（    ）A．不变 B．面积扩大为原来的3倍C．面积扩大为原来的9倍 D．面积缩小为原来的9、下列图案中既是轴对称图形，又是中心对称图形的是（    ）A．  B．C． D．10、如图图案中，不是中心对称图形的是（    ）A． B． C． D．第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、一条弧所对的圆心角为，弧长等于，则这条弧的半径为________．2、把一个正六边形绕其中心旋转，至少旋转________度，可以与自身重合．3、如图，在平面直角坐标系xOy中，P为x轴正半轴上一点．已知点，，为的外接圆．（1）点M的纵坐标为______；（2）当最大时，点P的坐标为______．4、在平面直角坐标系中，点关于原点对称的点的坐标是______．5、在平面直角坐标系中，将点绕坐标原点顺时针旋转后得到点Q，则点Q的坐标是___________．三、解答题（5小题，每小题10分，共计50分）1、如图，已知为的直径，切于点C，交的延长线于点D，且．（1）求的大小；（2）若，求的长．2、如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线AD交BC于点D，点E在AC上，以AE为直径的⊙O经过点D．（1）求证：①BC是⊙O的切线；②；（2）若点F是劣弧AD的中点，且CE＝3，试求阴影部分的面积．3、如图，AB是⊙O的直径，弦CD⊥AB于点E，AM是△ACD的外角∠DAF的平分线．（1）求证：AM是⊙O的切线；（2）连接CO并延长交AM于点N，若⊙O的半径为2，∠ANC = 30°，求CD的长．4、如图1，图2，图3的网格均由边长为1的小正方形组成，图1是三国时期吴国的数学家赵爽所绘制的“弦图”，它由四个形状、大小完全相同的直角三角形组成，赵爽利用这个“弦图”对勾股定理作出了证明，是中国古代数学的一项重要成就，请根据下列要求解答问题．（1）图1中的“弦图”的四个直角三角形组成的图形是　   　对称图形（填“轴”或“中心”）．（2）请将“弦图”中的四个直角三角形通过你所学过的图形变换，在图2，3的方格纸中设计另外两个不同的图案，画图要求：①每个直角三角形的顶点均在方格纸的格点上，且四个三角形互不重叠，不必涂阴影；②图2中所设计的图案（不含方格纸）必须是轴对称图形而不是中心对称图形；图3中所设计的图案（不含方格纸）必须既是轴对称图形，又是中心对称图形．5、如图，在平面直角坐标系中，经过原点，且与轴交于点，与轴交于点，点在第二象限上，且，则__． -参考答案-一、单选题1、A【分析】根据三角形旋转得出，，根据点A，D，E在同一条直线上利用邻补角关系求出，根据等腰三角形的性质即可得到∠DAC=50°，由此即可求解．【详解】证明：∵绕点C逆时针旋转得到，∴，，∴∠ADC=∠DAC，∵点A，D，E在同一条直线上，∴，∴∠DAC=50°，∴∠BAD=∠BAC-∠DAC=80°故选A．【点睛】本题考查三角形旋转性质，邻补角的性质，等腰三角形的性质与判定，解题的关键在于熟练掌握旋转的性质．2、D【分析】连接OB，OC，根据圆周角定理求出∠BOC的度数，再由OB=OC判断出△OBC是等边三角形，由此可得出结论．【详解】解：连接OB，OC，∵∠BAC=30°，∴∠BOC=60°．∵OB=OC，BC=6，∴△OBC是等边三角形，∴OB=BC=6．∴⊙O的直径等于12．故选：D．【点睛】本题考查的圆周角定理，根据题意作出辅助线，构造出等边三角形是解答此题的关键．3、B【分析】直接根据扇形的面积公式计算即可．【详解】故选：B．【点睛】本题考查了扇形的面积的计算，熟记扇形的面积公式是解题的关键．4、B【分析】根据“平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），即关于原点的对称点，横纵坐标都变成相反数”解答．【详解】解：点P（3，﹣2）关于原点O的对称点P'的坐标是（﹣3，2）．故选：B．【点睛】本题主要考查了关于原点对称的点的坐标的特点，正确掌握横纵坐标的关系是解题关键．5、B【分析】由题意以及旋转的性质可得为等边三角形，则BD=2，故CD=BC-BD=2．【详解】由题意以及旋转的性质知AD=AB，∠BAD=60°∴∠ADB=∠ABD∵∠ADB+∠ABD+∠BAD=180°∴∠ADB=∠ABD=60°故为等边三角形，即AB= AD =BD=2则CD=BC-BD=4-2=2故选：B．【点睛】本题考查了等边三角形的判定及性质，等边三角形的三边都相等，三个内角都相等，并且每一个内角都等于，等边三角形判定的方法有：三边相等的三角形是等边三角形（定义）；三个内角都相等的三角形是等边三角形；有一个内角是60度的等腰三角形是等边三角形；两个内角为60度的三角形是等边三角形．6、A【分析】取CB的中点G，连接MG，根据等边三角形的性质可得BH=BG，再求出∠HBN=∠MBG，根据旋转的性质可得MB=NB，然后利用“边角边”证明△MBG≌△NBH，再根据全等三角形对应边相等可得HN=MG，然后根据垂线段最短可得MG⊥CH时最短，再根据∠BCH=30°求解即可．【详解】解：如图，取BC的中点G，连接MG，∵旋转角为60°，∴∠MBH+∠HBN=60°，又∵∠MBH+∠MBC=∠ABC=60°，∴∠HBN=∠GBM，∵CH是等边△ABC的对称轴，∴HB=AB，∴HB=BG，又∵MB旋转到BN，∴BM=BN，在△MBG和△NBH中，，∴△MBG≌△NBH（SAS），∴MG=NH，根据垂线段最短，MG⊥CH时，MG最短，即HN最短，此时∵∠BCH=×60°=30°，CG=AB=×5=2.5，∴MG=CG=，∴HN=，故选A．【点睛】本题考查了旋转的性质，等边三角形的性质，全等三角形的判定与性质，垂线段最短的性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．7、B【分析】根据同弧所对的圆周角是圆心角的一半即可得．【详解】解：∵，∴，∴，故选：B．【点睛】题目主要考查圆周角定理，准确理解，熟练运用圆周角定理是解题关键．8、A【分析】设原来扇形的半径为r，圆心角为n，则变化后的扇形的半径为3r，圆心角为，利用扇形的面积公式即可计算得出它们的面积，从而进行比较即可得答案．【详解】设原来扇形的半径为r，圆心角为n，∴原来扇形的面积为，∵扇形的半径扩大为原来的3倍，圆心角缩小为原来的，∴变化后的扇形的半径为3r，圆心角为，∴变化后的扇形的面积为，∴扇形的面积不变．故选：A．【点睛】本题考查了扇形面积，熟练掌握并灵活运用扇形面积公式是解题关键．9、B【分析】根据中心对称图形与轴对称图形的概念逐项分析【详解】解：A. 是轴对称图形，不是中心对称图形，故该选项不正确，不符合题意；B. 既是轴对称图形，又是中心对称图形，故该选项正确，符合题意；C. 不是轴对称图形，是中心对称图形，故该选项不正确，不符合题意；D. 不是轴对称图形，是中心对称图形，故该选项不正确，不符合题意；故选B【点睛】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后两部分重合，掌握中心对称图形与轴对称图形的概念是解题的关键．10、C【分析】根据中心对称图形的概念：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心求解．【详解】解：A、是中心对称图形，故A选项不合题意；B、是中心对称图形，故B选项不合题意；C、不是中心对称图形，故C选项符合题意；D、是中心对称图形，故D选项不合题意；故选：C．【点睛】本题考查了中心对称图形的知识，解题的关键是掌握中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180°后重合．二、填空题1、9cm【分析】由弧长公式即可求得弧的半径．【详解】∵∴故答案为：9cm【点睛】本题考查了扇形的弧长公式，善于对弧长公式变形是关键．2、60【分析】正六边形连接各个顶点和中心，这些连线会将360°分成6分，每份60°因此至少旋转60°，正六边形就能与自身重合．【详解】360°÷6=60°故答案为：60【点睛】本题考查中心对称图形的性质，根据图形特征找到最少旋转度数是本题关键．3、5    (4，0)    【分析】（1）根据点M在线段AB的垂直平分线上求解即可；（2）点P在⊙M切点处时，最大，而四边形OPMD是矩形，由勾股定理求解即可．【详解】解：（1）∵⊙M为△ABP的外接圆，∴点M在线段AB的垂直平分线上，∵A(0，2)，B(0，8)，∴点M的纵坐标为：，故答案为：5；（2）过点，，作⊙M与x轴相切，则点M在切点处时，最大，理由：若点是x轴正半轴上异于切点P的任意一点，设交⊙M于点E，连接AE，则∠AEB=∠APB，∵∠AEB是ΔAE的外角，∴∠AEB>∠AB，∵∠APB>∠AB，即点P在切点处时，∠APB最大，∵⊙M经过点A(0，2)、B(0，8)，∴点M在线段AB的垂直平分线上，即点M在直线y=5上，∵⊙M与x轴相切于点P，ＭP⊥x轴，从而MP=5，即⊙M的半径为5，设AB的中点为D，连接MD、AM，如上图，则MD⊥AB，AD=BD=AB=3，BM=MP=5，而∠POD=90°，∴四边形OPMD是矩形，从而OP=MD，由勾股定理，得MD=，∴OP=MD=4，∴点P的坐标为(4，0)，故答案为：(4，0)．【点睛】本题考查了切线的性质，线段垂直平分线的性质，矩形的判定及勾股定理，正确作出图形是解题的关键．4、（3，4）【分析】关于原点对称的点，横坐标与纵坐标都互为相反数．【详解】：由题意，得点（-3，-4）关于原点对称的点的坐标是（3，4），故答案为：（3，4）．【点睛】本题考查了关于原点对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于原点对称的点，横坐标与纵坐标都互为相反数．5、【分析】绕坐标原点顺时针旋转即关于原点中心对称，找到关于原点中心对称的点的坐标即可，根据关于原点对称的两个点，横坐标、纵坐标分别互为相反数，即可求解．【详解】解：将点绕坐标原点顺时针旋转后得到点Q，则点Q的坐标是故答案为：【点睛】本题考查了求一个点关于原点中心对称的点的坐标，掌握关于原点中心对称的点的坐标特征是解题的关键．关于原点对称的两个点，横坐标、纵坐标分别互为相反数．三、解答题1、（1）45°（2）【分析】（1）连接OC，根据切线的性质得到OC⊥CD，根据圆周角定理得到∠DOC=2∠CAD，进而证明∠D=∠DOC，根据等腰直角三角形的性质求出∠D的度数；（2）根据等腰三角形的性质求出OC，根据弧长公式计算即可．（1）连接．∵ ，∴ ，即 ．∵ ，∴ ．∵ 是⊙的切线，∴ ，即 ．∴ ． ∴ ．∴ ．（2）∵ ，，∴ ．∵ ，∴ ．∴ 的长．【点睛】本题考查的是切线的性质、圆周角定理、弧长的计算，掌握圆的切线垂直于经过切点的半径是解题的关键．2、（1）①见解析；②见解析；（2）．【分析】（1）①连接OD，由角平分线的性质解得，再根据内错角相等，两直线平行，证明，继而由两直线平行，同旁内角互补证明即可解题；②连接DE，由弦切角定理得到，再证明，由相似三角形对应边成比例解题；（2）证明是等边三角形，四边形DOAF是菱形，，结合扇形面积公式解题．【详解】解：（1）①连接OD，是∠BAC的平分线是⊙O的切线；②连接DE，是⊙O的切线，是直径（2）连接DE、OD、DF、OF,设圆的半径为R，点F是劣弧AD的中点，OF是DA中垂线DF=AF，是等边三角形，四边形DOAF是菱形，．【点睛】本题考查圆的综合题，涉及切线的判定与性质、平行四边形的性质、等边三角形的判定与性质、相似三角形的判定与性质、扇形面积等知识，综合性较强，有难度，掌握相关知识是解题关键．3、（1）见解析（2）CD=2【分析】（1）由题意易得BC=BD，∠DAM=∠DAF，则有∠CAB=∠DAB，进而可得∠BAM=90°，然后问题可求证；（2）由题意易得CD//AM，∠ANC=∠OCE=30°，然后可得OE=1，CE=，进而问题可求解．（1）证明：∵AB是⊙O的直径，弦CD⊥AB于点E∴BC=BD∴∠CAB=∠DAB∵AM是∠DAF的平分线∴∠DAM=∠DAF∵∠CAD+∠DAF=180°∴∠DAB+∠DAM=90°即∠BAM=90°，AB⊥AM∴AM是⊙O的切线（2）解：∵AB⊥CD，AB⊥AM ∴CD//AM∴∠ANC=∠OCE=30°在Rt△OCE中，OC=2∴OE=1，CE=∵AB是⊙O的直径，弦CD⊥AB于点E∴CD=2CE=2．【点睛】本题主要考查切线的判定定理、垂径定理及含30度直角三角形的性质，熟练掌握切线的判定定理、垂径定理及含30度直角三角形的性质是解题的关键．4、（1）中心（2）见解析【分析】（1）利用中心对称图形的意义得到答案即可；（2）①每个直角三角形的顶点均在方格纸的格点上，且四个三角形不重叠，是轴对称图形；②所设计的图案（不含方格纸）必须是中心对称图形或轴对称图形．（1）图1中的“弦图”的四个直角三角形组成的图形是中心对称图形，故答案为：中心；（2）如图2是轴对称图形而不是中心对称图形；图3既是轴对称图形，又是中心对称图形．【点睛】本题考查利用旋转或轴对称设计方案，关键是理解旋转和轴对称的概念，按要求作图即可．5、2+【分析】连接AC，CM，AB，过点C作CH⊥OA于H，设OC=a．利用勾股定理构建方程解决问题即可．【详解】解：连接AC，CM，AB，过点C作CH⊥OA于H，设OC=a．∵∠AOB=90°，∴AB是直径，∵A（-4，0），B（0，2），∴，∵∠AMC=2∠AOC=120°，，在Rt△COH中，，，在Rt△ACH中，AC2=AH2+CH2，∴，∴a=2+ 或2-（因为OC＞OB，所以2-舍弃），∴OC=2+，故答案为：2+．【点睛】本题考查圆周角定理，勾股定理，解直角三角形等知识，解题的关键是学会利用参数构建方程解决问题．