初中数学人教版八年级下册18.2.3 正方形多媒体教学课件ppt

这是一份初中数学人教版八年级下册18.2.3 正方形多媒体教学课件ppt，共26页。PPT课件主要包含了学习目标，课时讲解，课时流程，课时导入，菱形的判别方法，矩形的判别方法，知识点，正方形的对称性，感悟新知，正方形的判定等内容，欢迎下载使用。
正方形的对称性正方形的判定
①有一个角是直角的平行四边形②有三个角是直角的四边形③对角线相等的平行四边形 ①有一组邻边相等的平行四边形②四条边都相等的四边形③对角线互相垂直的平行四边形
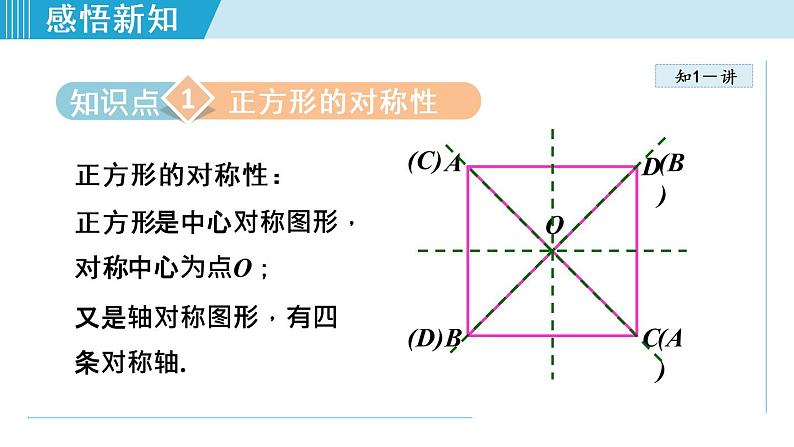
正方形的对称性：正方形是中心对称图形，对称中心为点O；又是轴对称图形，有四条对称轴.
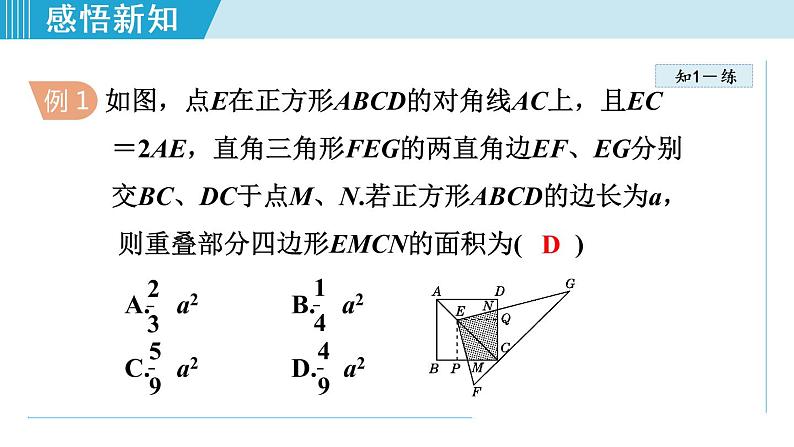
如图，点E在正方形ABCD的对角线AC上，且EC ＝2AE，直角三角形FEG的两直角边EF、EG分别 交BC、DC于点M、N.若正方形ABCD的边长为a， 则重叠部分四边形EMCN的面积为(　　) A. a2　　 B. a2　 　 C. a2　 　D. a2
作EP⊥BC于点P，EQ⊥CD于点Q，易得△EPM≌△EQN，利用四边形EMCN的面积等于正方形PCQE的面积求解．作EP⊥BC于点P，EQ⊥CD于点Q，∵四边形ABCD是正方形，∴∠BCD＝90°，又∵∠EPM＝∠EQN＝90°，∴∠PEQ＝90°，∴∠PEM＋∠MEQ＝90°，
∵三角形FEG是直角三角形，∴∠NEF＝∠NEQ＋∠MEQ＝90°，∴∠PEM＝∠NEQ，∵CA是∠BCD的角平分线，∠EPC＝∠EQC＝90°，∴EP＝EQ，四边形PCQE是正方形，
在△EPM和△EQN中，∴△EPM≌△EQN(ASA)，∴S△EQN＝S△EPM，
∴四边形EMCN的面积等于正方形PCQE的面积，∵正方形ABCD的边长为a，∴AC＝ a，∵EC＝2AE，∴EC＝ a，∴EP＝PC＝ a，∴正方形PCQE的面积＝ a× a＝ a2，∴四边形EMCN的面积＝ a2.
本例解法在于巧用割补法，将分散的图形拼合在一起，将不规则的阴影面积集中到一个规则的图形中，再利用正方形及三角形的性质求出，解答过程体现了割补法及转化思想．
小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了(　　)A．1次　 B．2次C．3次 D．4次
将五个边长都为2 cm的正方形按如图所示方式摆放，点A，B，C，D分别是四个正方形的中心，则图中四块阴影部分面积的和为(　　)A．2 cm2 B．4 cm2C．6 cm2 D．8 cm2
正方形是特殊的平行四边形，也是特殊的矩形，也是特殊的菱形.
如图，在△ABC中，∠ACB＝90°，CD平分 ∠ACB，DE⊥BC，DF⊥AC，垂足分别为E， F. 求证：四边形CFDE是正方形．
要证四边形CFDE是正方形，首先要确定这个正方形建立在哪种四边形的基础上，即先证它是什么四边形；再证这种四边形是正方形需要补充的条件．
∵DE⊥BC，AC⊥BC，∴DE∥CF. 同理DF∥CE ， ∴四边形CFDE是平行四边形． ∵CD平分∠ACB，DE⊥BC，DF⊥AC， ∴DE＝DF，∴▱ CFDE是菱形． ∵∠ACB＝90°，∴菱形CFDE是正方形．证法二：∵∠ECF＝∠CFD＝∠CED＝90°， ∴四边形CFDE是矩形． ∵CD平分∠ACB，DE⊥BC，DF⊥AC， ∴DE＝DF，∴矩形CFDE是正方形．
证明条件中不含对角线的四边形是正方形的四种方法：方法1：证：“四边形＋四边相等＋四个直角”；方法2：证：“平行四边形＋一组邻边相等＋一个直角”；方法3：证：“矩形＋一组邻边相等”；方法4：证：“菱形＋一个直角”．
如图，已知在▱ABCD中，对角线AC，BD交于点O， E是BD的延长线上的点，且EA＝EC. (1)求证：四边形ABCD是菱形； (2)若∠DAC＝∠EAD＋∠AED， 求证：四边形ABCD是正方形．
要证▱ABCD是正方形，有三种途径可走：即在平行四边形、菱形、矩形的基础上，找各需补充的对角线的条件进行证明；若要证明▱ABCD是菱形，由于题中条件与对角线相关，则需证AC⊥BD.
(1)首先根据平行四边形的性质可得AO＝CO，再由EA ＝EC可得△EAC是等腰三角形，然后根据等腰三角 形三线合一的性质可得EO⊥AC，根据对角线互相 垂直的平行四边形是菱形可证出结论；(2)首先根据角的关系得出AO＝DO，进而得到AC＝ BD，再根据对角线相等的菱形是正方形可得到结 论．
(1)∵四边形ABCD是平行四边形，∴AO＝CO， ∵EA＝EC，∴EO⊥AC，即BD⊥AC， ∴四边形ABCD是菱形．(2)∵∠ADO＝∠EAD＋∠AED， ∠DAC＝∠EAD＋∠AED， ∴∠ADO＝∠DAC，∴AO＝DO， ∵四边形ABCD是菱形，∴AC＝2AO，BD＝2DO， ∴AC＝BD，∴四边形ABCD是正方形.
证明条件中含对角线的四边形是正方形的方法：(1)证：“四边形＋对角线互相垂直、平分且相等”；(2)证：“平行四边形＋对角线互相垂直且相等”；(3)证：“矩形＋对角线互相垂直”；(4)证：“菱形＋对角线相等”．
满足下列条件的四边形是不是正方形？为什么？(1)对角线互相垂直且相等的平行四边形；(2)对角线互相垂直的矩形；(3)对角线相等的菱形；(4)对角线互相垂直平分且相等的四边形
(1)是；(2)是；(3)是；(4)是．原因略．
如图，在菱形ABCD中，对角线AC，BD相交于点O，不添加任何辅助线，请添加一个条件___________________________，使四边形ABCD是正方形．
∠BAD＝90°(答案不唯一)
下列判断错误的是(　　)A．两组对边分别相等的四边形是平行四边形B．四个内角都相等的四边形是矩形C．四条边都相等的四边形是菱形D．两条对角线垂直且互相平分的四边形是正 方形
小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB＝BC；②∠ABC＝90°；③AC＝BD；④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形(如图)，现有下列四种选法，你认为其中错误的是(　　) A．①② B．②③C．①③ D．②④
在△ABC中，点D，E，F分别在BC，AB，CA上，且DE∥CA，DF∥BA，连接EF，AD，则下列三种说法：①如果EF＝AD，那么四边形AEDF是矩形；②如果EF⊥AD，那么四边形AEDF是菱形；③如果AD⊥BC且AB＝AC，那么四边形AEDF是正方形，其中正确的有(　　)A．3个 B．2个 C．1个 D．0个