2021年北京大兴区北京市国际艺术学校（初中部）九年级上期末数学试卷

这是一份2021年北京大兴区北京市国际艺术学校（初中部）九年级上期末数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 在下列图形中，为中心对称图形的是
A. 等腰梯形B. 平行四边形C. 正五边形D. 等腰三角形

2. 下列事件属于必然事件的是
A. 打开电视，正在播放新闻
B. 我们班的同学将会有人成为航天员
C. 实数 a<0, 则 2a<0
D. 新疆的冬天不下雪

3. 将抛物线 y=2x+12−3 平移后与抛物线 y=2x2 重合，那么平移的方法可以是
A. 向右平移 1 个单位，再向上平移 3 个单位
B. 向右平移 1 个单位，再向下平移 3 个单位
C. 向左平移 1 个单位，再向上平移 3 个单位
D. 向左平移 1 个单位，再向下平移 3 个单位

4. 式子 2cs30∘−tan45∘−1−tan60∘2 的值是
A. 23−2B. 0C. 23D. 2

5. 如图，⊙O 的半径是 2，AB 是 ⊙O 的弦，点 P 是弦 AB 上的动点，且 1≤OP≤2，则弦 AB 所对的圆周角的度数是
A. 60∘B. 120∘C. 60∘ 或 120∘D. 30∘ 或 150∘

6. 如图，在平行四边形 ABCD 中，AB=4，∠BAD 的平分线与 BC 的延长线交于点 E，与 DC 交于点 F，且点 F 为边 DC 的中点，DG⊥AE，垂足为 G，若 DG=1，则 AE 的边长为
A. 23B. 43C. 4D. 8

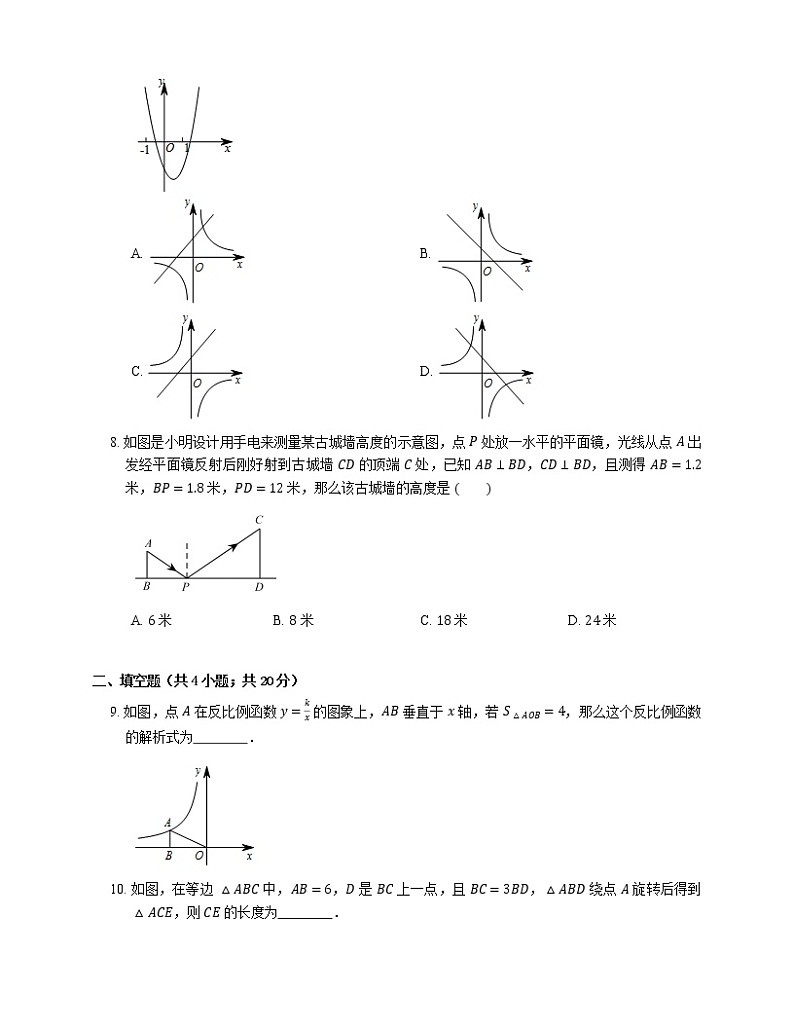
7. 二次函数 y=ax2+bx+c 的图象如图所示，则一次函数 y=bx+b2−4ac 与反比例函数 y=a+b+cx 在同一坐标系内的图象大致为
A. B.
C. D.

8. 如图是小明设计用手电来测量某古城墙高度的示意图，点 P 处放一水平的平面镜，光线从点 A 出发经平面镜反射后刚好射到古城墙 CD 的顶端 C 处，已知 AB⊥BD，CD⊥BD，且测得 AB=1.2 米，BP=1.8 米，PD=12 米，那么该古城墙的高度是
A. 6 米B. 8 米C. 18 米D. 24 米

二、填空题（共4小题；共20分）
9. 如图，点 A 在反比例函数 y=kx 的图象上，AB 垂直于 x 轴，若 S△AOB=4，那么这个反比例函数的解析式为 ．

10. 如图，在等边 △ABC 中，AB=6，D 是 BC 上一点，且 BC=3BD，△ABD 绕点 A 旋转后得到 △ACE，则 CE 的长度为 ．

11. 反比例函数 y=2a−1x 的图象有一支位于第一象限，则常数 a 的取值范围是 ．

12. 如图，在平面直角坐标系中，已知点 A3,0，B0,4，记 Rt△OAB 为三角形①，按图中所示的方法旋转三角形，依次得到三角形②，③，④，⋯⋯，则三角形⑤的直角顶点的坐标为 ；三角形⑩的直角顶点的坐标为 ；第2015个三角形的直角顶点的坐标为 ．

三、解答题（共13小题；共169分）
13. （1）已知 m=3，n=2，且 m（2）1−2+2−3+3−4+⋯+2014−2015．

14. 在平面直角坐标系中，等腰 Rt△OAB 斜边 OB 在 y 轴上，且 OB=4．
（1）画出 △OAB 绕原点 O 顺时针旋转 90∘ 后得到的三角形 △OAʹBʹ；
（2）求点 A 在旋转过程中经过的路径长．

15. 已知二次函数 y=x2+bx+c 的图象经过点 1,0 和 0,1．求这个二次函数的解析式，并求出它的图象的顶点坐标．

16. 如图，在以 O 为圆心的两个同心圆中，大圆的弦 AB 交小圆于 C，D 两点．求证：AC=BD．

17. 如图，在 △ABC 和 △ADE 中，ABAD=BCDE=ACAE，点 B，D，E 在一条直线上．求证：△ABD∽△ACE．

18. 已知：如图所示，AB 是 ⊙O 的直径，弦 CD⊥AB，垂足为 E，∠AOC=60∘，AC=2．
（1）求弦 CD 的长；
（2）求图中阴影部分的面积．

19. 某校学生会正筹备一个“庆毕业”文艺汇演活动，现准备从 4 名（其中两男两女）节目主持候选人中，随机选取两人担任节目主持人，请用列表法或画树状图求选出的两名主持人“恰好为一男一女”的概率．

20. 如图，山顶建有一座铁塔，塔高 CD=30 m，某人在点 A 处测得塔底 C 的仰角为 20∘，塔顶 D 的仰角为 23∘，求此人距 CD 的水平距离 AB．
（参考数据：sin20∘≈0.342，cs20∘≈0.940，tan20∘≈0.364，sin23∘≈0.391，cs23∘≈0.921，tan23∘≈0.424）

21. 如图，在 △ABC 中，∠BCA=90∘，以 BC 为直径的 ⊙O 交 AB 于点 P，Q 是 AC 的中点．
（1）求证：直线 PQ 与 ⊙O 相切；
（2）连接 PO 并延长交 ⊙O 于点 E，交 AC 的延长线于点 F，连接 PC，若 OC=5，tan∠OPC=12，求 EF 的长．

22. 如图，若 E 在 BC 的延长线上，其他条件不变，试探究 AE 与 EF 的数量关系．

23. 如图，二次函数 y=x2+bx+c 经过点 −1,0 和点 0,−3．
（1）求二次函数的表达式；
（2）如果一次函数 y=4x+m 的图象与二次函数的图象有且只有一个公共点，求 m 的值和该公共点的坐标；
（3）将二次函数图象 y 轴左侧部分沿 y 轴翻折，翻折后得到的图象与原图象剩余部分组成一个新的图象，该图象记为 G，如果直线 y=4x+n 与图象 G 有 3 个公共点，求 n 的值．

24. 如图，在平行四边形 ABCD 中，对角线 AC，BD 相交于点 O，点 E，F 是 AD 上的点，且 AE=EF=FD．连接 BE，BF．使它们分别与 AO 相交于点 G，H．
（1）求 EG:BG 的值；
（2）求证：AG=OG；
（3）设 AG=a，GH=b，HO=c，求 a:b:c 的值．

25. 如图 1，点 A 为抛物线 C1:y=12x2−2 的顶点，点 B 的坐标为 1,0，直线 AB 交抛物线 C1 于另一点 C．
（1）求点 C 的坐标；
（2）如图 1，平行于 y 轴的直线 x=3 交直线 AB 于点 D，交抛物线 C1 于点 E，平行于 y 轴的直线 x=a 交直线 AB 于 F，并抛物线 C1 于 G，若 FG:DE=4:3，求 a 的值；
（3）如图 2，将抛物线 C1 向下平移 mm>0 个单位得到抛物线 C2，且抛物线 C2 的顶点为点 P，交 x 轴负半轴于点 M，交射线 BC 于点 N.NQ⊥x 轴于点 Q，当 NP 平分 ∠MNQ 时，求 m 的值．
答案
第一部分
1. B
2. C
3. A
4. B
5. C
【解析】∵1≤OP≤2，
∴OP⊥AB 时，OP 长为 1．
∴∠AOB=2∠AOP=120∘．
∴ 弦 AB 所对的圆周角的度数是 60∘ 或 120∘．
6. B【解析】提示：
∵ 平行四边形 ABCD，且点 F 为边 DC 的中点，
易证 △ADF≌△ECF．
∴EF=FA，EC=BC=AD．
∵AE 平分 ∠BAD，
∴∠DAE=∠BAE=∠E，∠DAF=∠FAB=∠DFA，
∴AB=BE=4，AD=DF．
∵DG⊥AE，
∴AG=FG，
∴AD=2．
∵DG=1，
∴AG=3，
∴AE=43．
7. D【解析】由二次函数 y=ax2+bx+c 的图象可知：
a>0，b<0，b2−4ac>0，
当 x=1，y=a+b+c<0．
∴ 反比例函数 y=a+b+cx 的图象分布在二、四象限，可以先排除A、B；
∵y=bx+b2−4ac 中，b<0，b2−4ac>0，
∴ 一次函数 y=bx+b2−4ac 经过一、二、四象限，排除C，
∴ 选择D．
8. B【解析】由已知得 △ABP∽△CDP，则根据相似的性质可得 ABBP=CDPD，解答即可．
第二部分
9. y=−8x
10. 2
【解析】在等边 △ABC 中，AB=6，
∴BC=AB=6，
∵BC=3BD，
∴BD=2，
∵△ABD 绕点 A 旋转后得到 △ACE，
∴△ABD≌△ACE，
∴CE=BD=2．
11. a>12
【解析】∵ 反比例函数 y=2a−1x 的图象有一支位于第一象限，
∴2a−1>0，解得 a>12．
12. 845,125，36,0，402845,125
【解析】
如图，过 C 作 CD⊥AB 于点 D．
在 Rt△ABC 中，AC=3，BC=4，根据勾股定理，可得 AB=5，利用面积可知，CD=125．
在 Rt△ACD 中，根据勾股定理，可得 AD=95．
①中直角顶点为 0,0；
②中直角顶点为 0+3+95,125；
③中直角顶点为 3+5+4,0；
经过 3 次旋转之后，直角三角形重新回到①的状态．横坐标为 3+5+4=12，纵坐标为 0．所以
④中直角顶点为 12,0；
⑤中直角顶点为 12+3+95,125；
⑥中直角顶点为 12×2,0．
由此可知三角形⑩的直角顶点与①状态相同，且 10=3×3+1，
所以⑩中直角顶点为 12×3,0．
因为 2015=3×671+2，
同理可得第2015个三角形的顶点坐标 12×671+3+95,125．
第三部分
13. （1） ∵m=3，
∴m=±3，
∵n=2，
∴n=±2，
∵m ∴m=−3，n=±2．
当 m=−3，n=−2 时，m2+mn+n2=9+6+4=19；
当 m=−3，n=2 时，m2+mn+n2=9−6+4=7．
（2） 原式=2−1+3−2+4−3+⋯+2015−2014=2015−1.
14. （1） 画图正确（如图）
（2） ∵ 等腰直角 △ABO，OB=4，
∴OA=22，
∴ 点 A 的路径长为 2π．
15. 根据题意，得 1+b+c=0,c=1. 解得 b=−2,c=1.
所以所求的二次函数的解析式为 y=x2−2x+1．
又因为 y=x2−2x+1=x−12，
所以函数图象的顶点坐标是 1,0．
16. 过点 O 作 OE⊥AB 于点 E．
∵O 为圆心，且 OE⊥AB．
∴AE=BE，
同理 CE=DE．
∴AC=BD．
17. ∵ 在 △ABC 和 △ADE 中，ABAD=BCDE=ACAE，
∴ △ABC∽△ADE，
∴ ∠BAC=∠DAE，
∴ ∠BAD=∠CAE．
∵ ABAD=ACAE，
∴ ABAC=ADAE，
∴ △ABD∽△ACE．
18. （1） ∵ AB 是 ⊙O 的直径，
∴ ∠ACB=90∘．
∵ AC=2，∠AOC=60∘，
∴ △AOC 是等边三角形，
则 AO=AC=2，AB=4，∠CAE=60∘．
∵ 弦 CD⊥AB，
∴ AE=1
∴ CE=DE=3．
∴ CD=23．
（2） ∵ S△ABC=12AB⋅CE=12×4×3=23，
∴ S阴影=S半圆−S△ABC=12π⋅22−23=2π−23．
19. 列表如下：
男男女女男−−−男,男女,男女,男男男,男−−−女,男女,男女男,女男,女−−−女,女女男,女男,女女,女−−−
所有等可能的情况有 12 种，其中选出的两名主持人“恰好为一男一女”的情况有 8 种，则 P （ 选出的两名主持人
“恰好为一男一女”） =812=23 .
20. 在 Rt△ABC 中，∠CAB=20∘，
∴BC=AB⋅tan∠CAB=AB⋅tan20∘．
在 Rt△ABD 中，∠DAB=23∘，
∴BD=AB⋅tan∠DAB=AB⋅tan23∘．
∴CD=BD−BC=AB⋅tan23∘−AB⋅tan20∘=ABtan23∘−tan20∘.
∴AB=CDtan23∘−tan20∘≈300.424−0.364=500m.
答：此人距 CD 的水平距离 AB 约为 500 m．
21. （1） 连接 PO，PC．
∵BC 是 ⊙O 的直径，
∴∠BPC=90∘．
则 ∠APC=90∘．
∵CQ=AQ，
∴PQ=12AC=CQ．
∴∠CPQ=∠PCQ．
∵OP=OC，
∴∠OPC=∠OCP，
∴∠OPC+∠CPQ=∠OCP+∠PCQ=∠BCA=90∘，
∴ 直线 PQ 与 ⊙O 相切．
（2） 连接 CE．
∵EP 是直径，
∴∠ECP=90∘．
∠ECO+∠OCP=90∘．
∵∠ECO+∠ECF=90∘，
∴∠ECF=∠OCP=∠OPC，∠F=∠F，
△EFC∽△CFP．
∴EFCF=CFPF．
Rt△ECP，tan∠EPC=12，
∴CECP=12．
EFCF=CFPF=12，
∴CF=2EF，PF=2CF=4EF，
∴PE=3EF=2OC=25，
∴EF=253．
22. AE=EF，
在 BA 的延长线上截取 AG=CE，
证 △AGE≌△ECF．
23. （1） 把 −1,0 和 0,−3 代入到 y=x2+bx+c 中，得
0=1−b+c,−3=c,
解得
b=−2,c=−3,
所以 y=x2−2x−3．
（2） 由题意得
y=x2−2x−3,y=4x+m,
∴x2−6x−3+m=0，
∴Δ=−62+43+m=0，
∴m=−12，
∴y=x2−2x−3,y=4x−12, 解得
x=3,y=0,
∴m=−12，公共点为 3,0．
（3）
原抛物线解析式为 y=x2−2x−3，原抛物线沿 y 轴翻折后得到的新抛物线：y=x2+2x−3，由 y=x2+2x−3,y=4x+n, 得
x2−2x−3−n=0,
∴Δ=−22+43+n=0，
∴n=−4，
将 0,−3 代入到 y=4x+n 中，得 n=−3．
综上，n=−3 或 n=−4．
24. （1） ∵ 四边形 ABCD 是平行四边形，
∴AO=12AC，AD=BC，AD∥BC．
∴△AEG∽△CBG．
∴EGGB=AGGC=AEBC．
∵AE=EF=FD，
∴BC=AD=3AE．
∴GC=3AG，GB=3EG．
∴EG:BG=1:3．
（2） ∵GC=3AG（已证），
∴AC=4AG．
∴AO=12AC=2AG．
∴GO=AO−AG=AG．
（3） ∵AE=EF=FD，
∴BC=AD=3AE，AF=2AE．
∵AD∥BC，
∴△AFH∽△CBH．
∴AHHC=AFBC=2AE3AE=23．
∴AHAC=25，即 AH=25AC．
∵AC=4AG，
∴a=AG=14AC，b=AH−AG=25AC−14AC=320AC，c=AO−AH=12AC−25AC=110AC．
∴a:b:c=14:320:110=5:3:2．
25. （1） 当 x=0 时，y=−2，
∴A0,−2．
设直线 AB 的解析式为 y=kx+b，则
−2=b,0=k+b.
解得
k=2,b=−2.
∴ 直线 AB 的解析式为 y=2x−2．
∵ 点 C 为直线 y=2x−2 与抛物线 y=12x2−2 的交点，则点 C 的横、纵坐标满足
y=12x2−2,y=2x−2.
解得
x1=4,y1=6, x2=0,y2=−2.舍
∴ 点 C 的坐标为 4,6．
（2）
直线 x=3 分别交直线 AB 和抛物线 C1 于 D，E 两点，
∴yD=4，yE=52，
∴DE=32．
∵FG:DE=4:3，
∴FG=2．
∵ 直线 x=a 分别交直线 AB 和抛物线 C1 于 F，G 两点．
∴yF=2a−2，yG=12a2−2，
∴FG=2a−12a2=2．
解得 a1=2，a2=2+22，a3=2−22．
（3）
解法一：
设直线 MN 交 y 轴于 T，过点 N 作 NH⊥y 轴于点 H．
设点 M 的坐标为 t,0，抛物线 C2 的解析式为 y=12x2−2−m．
∴0=12t2−2−m．
∴−2−m=−12t2．
∴y=12x2−12t2．
∴ 点 P 坐标为 0,−12t2．
∵ 点 N 是直线 AB 与抛物线 y=12x2−12t2 的交点，则点 N 的横、纵坐标满足
y=12x2−12t2,y=2x−2.
解得
x1=2−t,y1=2−2t, x2=2+t,y2=2+2t.舍
∴N2−t,2−2t．
∴MQ=NQ=2−2t．
∴∠NMQ=45∘，
∴△MOT，△NHT 均为等腰直角三角形．
∴MO=TO，HT=HN．
∴OT=−t，NT=2NH=22−t，PT=−t+12t2．
∵PN 平分 ∠MNQ，
∴PT=NT，
∴−t+12t2=22−t．
∴t1=−22，t2=2（舍）．
∴−2−m=−12t2=−12−222，
∴m=2．
解法二：
设 N 坐标为 t,2t−2，抛物线 C2 的解析式为 y=12x2−2−m．
∴2t−2=12t2−2−m．
∴ 点 P 坐标为 0,−12t2+2t−2．
同解法一可得 ∠MNQ=45∘，
∴∠PNQ=12∠MNQ=22.5∘．
过点 P 作 PF⊥NQ 于点 F，在 FN 上截取 FJ=FP，连接 JP．
∴NJ=JP=2PF=2FJ．
∴NF=2+1PF，
即 2t−2−−12t2+2t−2=2+1t，
∴t1=22+2，t2=0（舍）．
∴m=12t2−2t=2．