2021年安徽歙县黄山市歙县横关学校八年级下期末数学试卷

这是一份2021年安徽歙县黄山市歙县横关学校八年级下期末数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 下列二次根式中，是最简二次根式的是
A. 0.2B. 25xyC. 6ab3D. a2+1

2. 在四边形 ABCD 中，从① AB∥CD；② AB=CD；③ BC∥AD；④ BC=AD 中任选两个使四边形 ABCD 为平行四边形的选法有 种．
A. 3B. 4C. 5D. 6

3. 要使代数式 1−xx+2 有意义，则 x 的取值范围是
A. x≥1B. x≤1
C. x≥1 且 x≠−2D. x≤1 且 x≠−2

4. 下列命题中的真命题是
A. 有一组对边平行的四边形是平行四边形
B. 有一个角是直角的四边形是矩形
C. 顺次连接矩形各中点所得的四边形是菱形
D. 对角线互相垂直平分的四边形是正方形

5. 正方形 A1B1C1O，A2B2C2C1，A3B3C3C2，⋯ 按如图的方式放置．点 A1，A2，A3，⋯ 和点 C1，C2，C3，⋯ 分别在直线 y=x+1 和 x 轴上，则点 B2016 的纵坐标是
A. 22013B. 22014C. 22015D. 22016

6. 一家鞋店在一段时间内销售了某种女鞋 30 双，各种尺码的鞋销售量如下表：
尺码销售量/双12510462
店主决定在下次进货时增加一些 23.5 cm 尺码的女鞋，影响店主决策的统计量是
A. 平均数B. 中位数C. 众数D. 方差

7. 化简二次根式 32×2 得
A. −32B. 32C. ±32D. 6

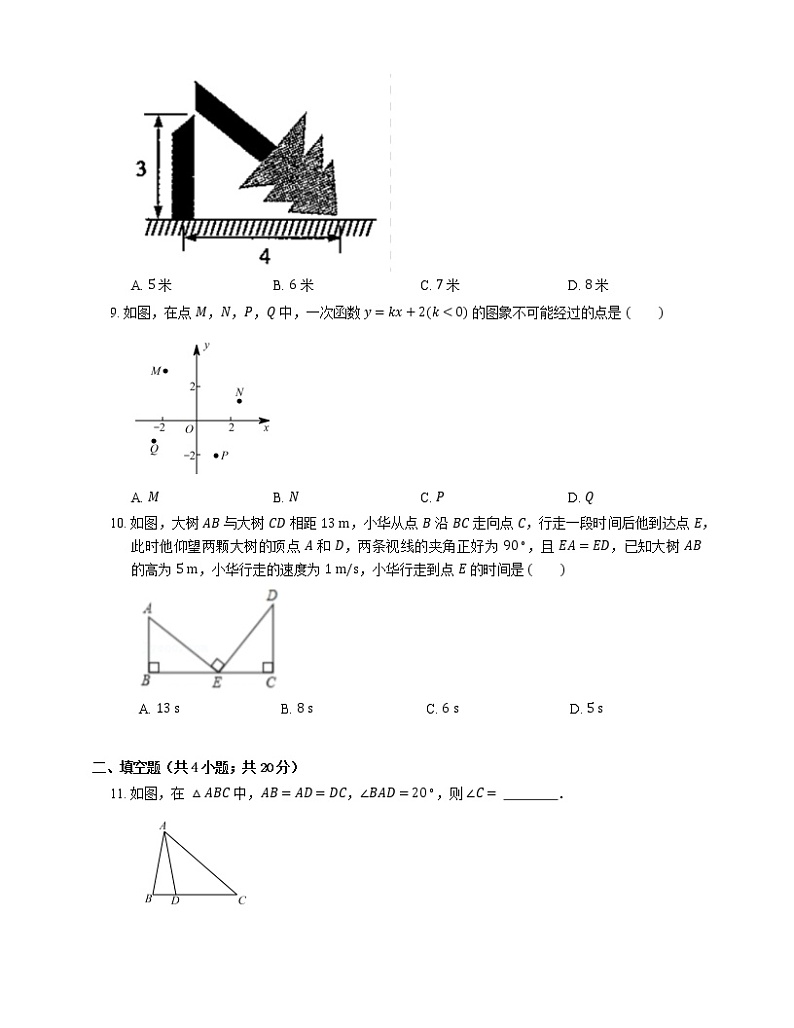
8. 如图，一次飓风灾害中，一棵大树在离地面 3 米处折断，树的顶端落在离树干底部 4 米处，那么这棵树折断之前的高度是
A. 5 米B. 6 米C. 7 米D. 8 米

9. 如图，在点 M，N，P，Q 中，一次函数 y=kx+2k<0 的图象不可能经过的点是
A. MB. NC. PD. Q

10. 如图，大树 AB 与大树 CD 相距 13 m，小华从点 B 沿 BC 走向点 C，行走一段时间后他到达点 E，此时他仰望两颗大树的顶点 A 和 D，两条视线的夹角正好为 90∘，且 EA=ED，已知大树 AB 的高为 5 m，小华行走的速度为 1 m/s，小华行走到点 E 的时间是
A. 13 sB. 8 sC. 6 sD. 5 s

二、填空题（共4小题；共20分）
11. 如图，在 △ABC 中，AB=AD=DC，∠BAD=20∘，则 ∠C= ．

12. 某一次函数的图象经过点 −1,3，且函数值 y 随 x 的增大而减小，请你写出一个符合条件的函数解析式 ．

13. 如图，一个底面周长为 24 cm，高为 5 cm 的圆柱体，一只蚂蚁沿侧表面从点 A 到点 B 所经过的最短路线长为 ．

14. 如图，△ABC 是等腰三角形，∠C=90∘，D 是 AB 的中点，点 E，F 分别在 AC，BC 边上运动（点 E 不与点 A，C 重合），且保持 AE=CF，连接 DE，DF，EF．在此运动变化过程中，有下列结论：
① DE=DF；
② ∠EDF=90∘；
③四边形 CEDF 不可能为正方形；
④四边形 CEDF 的面积保持不变．
一定成立的结论有 ．（把你认为正确的序号都填上）

三、解答题（共9小题；共117分）
15. 计算：20−0.5−218+5．

16. 如图，把长方形纸片 ABCD 沿 EF 折叠后，点 D 与点 B 重合，点 C 落在点 Cʹ 的位置上，若 ∠BFE=67.5∘，AE=2．
（1）求 ∠AEB 的度数；
（2）求长方形纸片 ABCD 的面积．

17. 如图，在 Rt△ABC 中，∠ACB=90∘，DE，DF 是 △ABC 的中位线，连接 EF，CD．求证：EF=CD．

18. 某市篮球队到市一中选拔一名队员，教练对王亮和李刚两名同学进行 5 次 3 分投篮测试，每人每次投 10 个球，如图记录的是这两名同学 5 次投篮中所投中的个数．
（1）请你根据图中的数据，填写表格；
姓名平均数众数方差王亮7李刚72.8
（2）若你是教练，你打算选谁?简要说明理由．

19. A县和B县分别有某种库存机器 6 台和 12 台，现决定支援C村 10 台，D村 8 台，已知从A县调运一台机器到C村和D村的运费分别是 300 元和 500 元；从B县调运一台机器到C村和D村的运费分别是 400 元和 800 元．
（1）设A县运往C村机器 x 台，求总运费 y（元）关于 x 的函数关系式；
（2）若要求总运费不超过 9000 元，共有几种调运方案?哪种调运方案运费最低?

20. 甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长 y（米）与时间 x（时）的函数图象为线段 OA，乙队铺设完的路面长 y（米）与时间 x（时）的函数图象为折线 BC−−CD−−DE，如图所示，从甲队开始工作时计时．
（1）直接写出乙队铺设完的路面长 y（米）与时间 x（时）的函数关系式；
（2）当甲队清理完路面时，乙队还有多少米的路面没有铺设完?

21. 已知 O 是坐标原点，点 A 的坐标是 5,0，点 B 是 y 轴正半轴上一动点，以 OB，OA 为边作矩形 OBCA，点 E，H 分别在边 BC 和边 OA 上，将 △BOE 沿着 OE 对折，使点 B 落在 OC 上的 F 点处，将 △ACH 沿着 CH 对折，使点 A 落在 OC 上的 G 点处．
（1）求证：四边形 OECH 是平行四边形；
（2）当点 B 运动到使得点 F，G 重合时，求点 B 的坐标，并判断四边形 OECH 是什么四边形?说明理由；
（3）当点 B 运动到使得点 F，G 将对角线 OC 三等分时，求点 B 的坐标．

22. 阅读下列材料，然后回答问题．在进行二次根式化简时，我们有时会碰上如 23+1 这样的式子，其实我们还可以将其进一步化简：
23+1=2×3−13+13−1=23−132−12=3−1,
以上这种化简的步骤叫做分母有理化．参照上面的方法化简：25+3．

23. 如图，等边三角形 ABC 的边长为 4，E 为边 AB 上一点，过点 E 作 DE⊥BC，交 BC 于点 D，在 DE 右侧作等边三角形 DEP，记 P 到 BC 的距离为 m1，P 到 AC 的距离为 m2．
（1）若 BD=43 试求线段 DE 的长，并求 m1，m2 的值．
（2）若 BD=x1≤x≤2，用含 x 的代数式表示 m1，m2，并求 P 在 ∠C 的平分线上时 x 的值．
答案
第一部分
1. D
2. B
3. D
4. C
5. C
6. C【解析】由表中数据知，这组数据的众数为 23.5 cm，所以影响店主决策的统计量是众数，故选C．
7. B
8. D
9. D
10. B
【解析】∵∠AED=90∘，
∴∠AEB+∠DEC=90∘，
∵∠ABE=90∘，
∴∠A+∠AEB=90∘，
∴∠A=∠DEC，
在 △ABE 和 △DCE 中，
∠B=∠C,∠A=∠DEC,AE=DE,
∴△ABE≌△ECDAAS，
∴EC=AB=5 m，
∵BC=13 m，
∴BE=8 m，
∴ 小华走的时间是 8÷1=8s．
第二部分
11. 40∘
【解析】∵AB=AD，∠BAD=20∘，
∴∠B=12180∘−∠BAD=12180∘−20∘=80∘．
∵∠ADC 是 △ABD 的外角，
∴∠ADC=∠B+∠BAD=80∘+20∘=100∘．
∵AD=DC．
∴∠C=12180∘−∠ADC=12180∘−100∘=40∘．
12. y=−x+2（答案不唯一）
13. 13 cm
14. ①②④
第三部分
15. 原式=25−22−2×24−5=5−2.
16. （1） ∵AD∥BC，
∴∠DEF=∠BFE=67.5∘，
又 ∵∠BEF=∠DEF=67.5∘，
∴∠AEB=180∘−∠BEF−∠DEF=180∘−67.5∘−67.5∘=45∘.
（2） 在直角 △ABE 中，由（1）知 ∠AEB=45∘，
∴∠ABE=90∘−∠AEB=90∘−45∘=45∘，
∴AB=AE=2，
∴BE=AB2+AE2=22+22=22，
又 ∵AD=AE+DE=AE+BE=2+22，
∴ 长方形纸片 ABCD 的面积为：AB×AD=2×2+22=4+42．
17. ∵DE，DF 是 △ABC 的中位线，
∴DE∥BC，DF∥AC，
∴ 四边形 DECF 是平行四边形．
又 ∵∠ACB=90∘，
∴ 四边形 DECF 是矩形，
∴EF=CD．
18. （1） 7；0.4；7
【解析】李刚 5 次投篮，有 2 次投中 7 个，故 7 为众数；
王亮的方差为 s2=156−72+7−72+8−72+7−72+7−72=0.4，
王亮的平均数为：6+7+8+7+7÷5=7．
（2） 打算选王亮．
因为两人的平均数、众数相同，从方差上看，王亮投篮成绩的方差小于李刚投篮成绩的方差．王亮的成绩较稳定．
19. （1） y=300x+5006−x+40010−x+80012−10−x=200x+8600．
（2） 因运费不超过 9000 元，
∴ y=200x+8600≤9000，
解得 x≤2．
∵ 0≤x≤6，
∴ 0≤x≤2．
则 x=0,1,2，
∴ 有三种调运方案．
当 x=0 时，调运运费最低．
20. （1） y=25x−75,3≤x<550,5≤x<6.525x−112.5,6.5≤x≤10.9．
【解析】设线段 BC 所在直线对应的函数关系式为 y=k1x+b1．
因为图象经过 3,0，5,50，
所以 3k1+b1=0,5k1+b1=50, 解得：k1=25,b1=−75.
所以线段 BC 所在直线对应的函数关系式为 y=25x−75．
设线段 DE 所在直线对应的函数关系式为 y=k2x+b2．
因为乙队按停工前的工作效率为：50÷5−3=25（米/时），
所以乙队剩下的需要的时间为：160−50÷25=225（时），
6.5+225=10.9（时）．
所以 E10.9,160，
所以 50=6.5k2+b2,160=10.9k2+b2, 解得：k2=25,b2=−112.5.
所以线段 DE 所在直线对应的函数关系式为 y=25x−112.5．
乙队铺设完的路面长 y（米）与时间 x（时）的函数关系式为
y=25x−75,3≤x<550,5≤x<6.525x−112.5,6.5≤x≤10.9．
（2） 由题意，得甲队每小时清理路面的长为 100÷5=20（米），
甲队清理完路面的时间为 160÷20=8（时）．
把 x=8 代入 y=25x−112.5，得 y=25×8−112.5=87.5．
当甲队清理完路面时，乙队铺设完的路面长为 87.5 米，
160−87.5=72.5（米），
答：当甲队清理完路面时，乙队还有 72.5 米的路面没有铺设完．
21. （1） ∵ 四边形 OBCA 为矩形，
∴OB∥CA，BC∥OA，
∴∠BOC=∠OCA，
又 ∵△BOE 沿着 OE 对折，使点 B 落在 OC 上的 F 点处；△ACH 沿着 CH 对折，使点 A 落在 OC 上的 G 点处，
∴∠BOC=2∠EOC，∠OCA=2∠OCH，
∴∠EOC=∠OCH，
∴OE∥CH，
又 ∵BC∥OA，
∴ 四边形 OECH 是平行四边形．
（2） 点 B 的坐标是 0,533；四边形 OECH 是菱形．理由如下：
∵△BOE 沿着 OE 对折，使点 B 落在 OC 上的 F 点处；△ACH 沿着 CH 对折，使点 A 落在 OC 上的 G 点处，
∴∠EFO=∠EBO=90∘，∠CFH=∠CAH=90∘，
∵ 点 F，G 重合，
∴EH⊥OC，
又 ∵ 四边形 OECH 是平行四边形，
∴ 平行四边形 OECH 是菱形，
∴EO=EC，
∴∠EOC=∠ECO，
又 ∵∠EOC=∠BOE，
∴∠EOB=∠EOC=∠ECO=30∘，
又 ∵ 点 A 的坐标是 5,0，
∴OA=5，
∴BC=5，
在 Rt△OBC 中，OB=33BC=533，
∴ 点 B 的坐标是 0,533．
（3） 当点 F 在点 O，G 之间时，
∵△BOE 沿着 OE 对折，使点 B 落在 OC 上的 F 点处；△ACH 沿着 CH 对折，使点 A 落在 OC 上的 G 点处，
∴OF=OB，CG=CA，
而 OB=CA，
∴OF=CG，
∵ 点 F，G 将对角线 OC 三等分，
∴AC=OF=FG=GC，
设 AC=m，则 OC=3m，
在 Rt△OAC 中，OA=5，
∵AC2+OA2=OC2，
∴m2+52=3m2，解得 m=542，
∴OB=AC=524，
∴ 点 B 的坐标是 0,542；
当点 G 在点 O，F 之间时，如图，
同理可得 OF=CG=AC，
设 OG=n，则 AC=GC=2n，
在 Rt△OAC 中，OA=5，
∵AC2+OA2=OC2，
∴2n2+52=3n2，解得 n=5，
∴AC=OB=25，
∴ 点 B 的坐标是 0,25．
综上所述，点 B 的坐标为 0,25 或 0,542．
22. 25+3=25−35+35−3=25−352−32=5−3.
23. （1） ∵△ABC 为等边三角形，
∴∠B=60∘，
∵DE⊥AC，
在 Rt△BDE 中，∠B=60∘，∠BDE=90∘，
∴∠BED=∠BDE−∠B=90∘−60∘=30∘，
∴BE=2BD=2×43=83，
∴DE=BE2−BD2=832−432=433，
延长 DP 与 AC 相交于点 F，如图 1 所示：
∵△EDP 为等边三角形，
∴∠EDP=∠EDF=60∘，
∵ED⊥BC，
∴∠EDB=90∘，
∴∠FDC=180∘−∠EDB−∠EDF=180∘−90∘−60∘=30∘,
∵∠C=60∘，
在 △DFC 中，∠DFC=180∘−∠FDC−∠C=180∘−60∘−30∘=90∘，
∴DF⊥FC 即 △DFC 为直角三角形，
∵BD=43，BC=4，
∴DC=BC−BD=4−43=83，
∴ 在 Rt△DFC 中，DC=83，∠CDF=30∘，
∴CF=12DC=43，
DF=DC2−CF2=832−432=433，
∴DF=DE，
∵DE=DP，
∴DF=DP，即点 F 与点 P 重合，
∴m2=0，
过点 P 作 PM⊥BC 交 BC 于点 M，如图 2 所示：
在 Rt△DMP 中，DF=433，∠PDM=30∘，
∴PM=12，DF=233，
∴m1=233，
∴m1⋅m2=0．
（2） 由（ 1 ）可知，当 BD=43 时，点 P 位于边 AC 上，
∴ 当 1≤x≤43 时，△DEP 在 △ABC 的内部，
当 43 △DEP 与 △ABC 部分重合，
①当 1≤x≤43，延长 DP 与 AC 相交于点 F，过点 P 作 PM⊥BC 交 BC 于点 M，如图 3 所示∶
∵ED⊥BC，
∴∠EDB=90∘，
∵△ABC 为等边三角形，
∴∠A=∠C=60∘，
在 Rt△EDB 中，∠BED=90∘−∠B=90∘−60∘=30∘，
∵BD=x，
∴BE=2x，
则 DE=BE2−BD2=2x2−x2=3x，
∵△EDP 为等边三角形，
∴ED=DP=3x，∠EDP=60∘，
∴∠FDC=180∘−∠EDB−∠EDP=180∘−90∘−60∘=30∘，
∵PM⊥BC，
∴ 在 Rt△PMD 中，DP=3x，∠PDM=30∘，
∴PM=12DP=3x2，
∴m1=32x，
∵∠FDC=30∘，∠C=60∘，
∴△DFC 中，
∠DFC=180∘−∠FDC−∠C=180∘−30∘−60∘=90∘,
∴DF⊥AC，
∴m2=DF，
在 Rt△DFC 中，∠FDC=30∘，DC=BC−BD=4−x，
∴FC=12DC=4−x2，
∴DF=DC2−FC2=4−x2−4x22=34−x2，
∴PF=DF−DP=324−x−3x=23−3x2，
∴m2=23−332x，
②当 43由①知 ED=DP=3x，DP⊥AC，∠PDC=30∘，
在 Rt△PND 中，∠PDC=30∘，
PN=12DP=32x，
∴m1=32x，
在 Rt△DHC 中，∠DHC=90∘，∠PDC=30∘，
DC=BC−BD=4−x，
∴HC=12DC=4x2，
DH=DC2−HC2=4−x2−4x22=34−x2，
HP=DP−DH=3x−324−x=332x−23,
∴m2=33x2−23，
当 P 在 ∠C 的平分线上时，
则 △DEP 在 △ABC 的内部，
根据角平分线性质，m1=m2，
∴32x=23−332x，x=1，
∴ 当 P 在 ∠C 的平分线上时，x=1．