

黑龙江省齐齐哈尔市铁锋区2021-2022学年九年级上学期期末数学试卷(word版 含答案)
展开
这是一份黑龙江省齐齐哈尔市铁锋区2021-2022学年九年级上学期期末数学试卷(word版 含答案),共30页。试卷主要包含了下列事件中,为必然事件的是,已知点A等内容,欢迎下载使用。
2021-2022学年黑龙江省齐齐哈尔市铁锋区九年级第一学期期末数学试卷
一.选择题
1.垃圾分类一小步,低碳生活一大步,垃圾桶上常有以下四种垃圾分类标识的图案和文字说明,其中图案是中心对称图形的是( )
A.有害垃圾 B.厨余垃圾 C.其它垃圾 D.可回收物
2.下列方程中是关于x的一元二次方程的是( )
A. B.ax2+bx+c=0
C.(x﹣1)(x﹣2)=0 D.3x2+2=x2+2(x﹣1)2
3.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
A.(3,3) B.(4,3) C.(3,1) D.(4,1)
4.下列事件中,为必然事件的是( )
A.明天要下雨
B.太阳从东边升起
C.﹣2>﹣1
D.打开电视机,它正在播广告
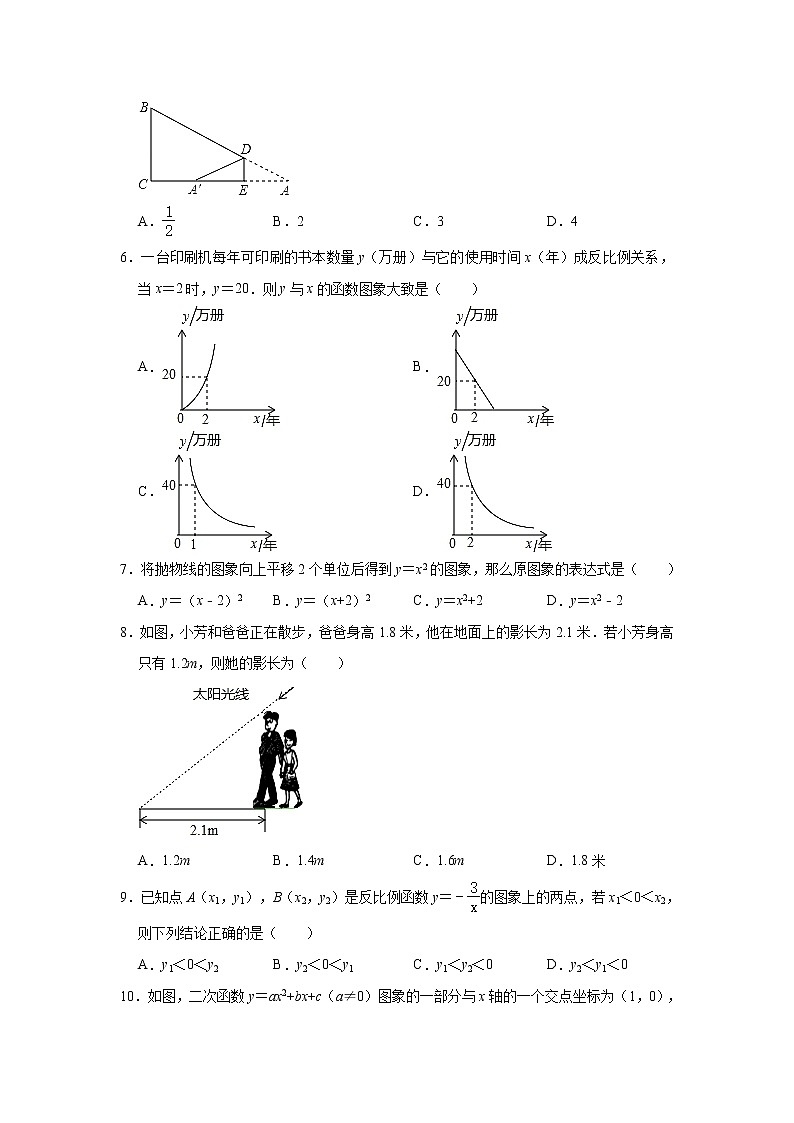
5.如图,在△ABC 中,∠C=90°,BC=6,D,E 分别在 AB、AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
A. B.2 C.3 D.4
6.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
7.将抛物线的图象向上平移2个单位后得到y=x2的图象,那么原图象的表达式是( )
A.y=(x﹣2)2 B.y=(x+2)2 C.y=x2+2 D.y=x2﹣2
8.如图,小芳和爸爸正在散步,爸爸身高1.8米,他在地面上的影长为2.1米.若小芳身高只有1.2m,则她的影长为( )
A.1.2m B.1.4m C.1.6m D.1.8米
9.已知点A(x1,y1),B(x2,y2)是反比例函数y=﹣的图象上的两点,若x1<0<x2,则下列结论正确的是( )
A.y1<0<y2 B.y2<0<y1 C.y1<y2<0 D.y2<y1<0
10.如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图象给出下列结论:
①a+b+c=0;
②a﹣2b+c<0;
③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;
④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;
⑤a﹣b<m(am+b)(m为任意实数).
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.若一元二次方程的二次项系数为1,常数项为0,它的一个根为2,则该方程为 .
12.一个圆锥的侧面展开图是半圆,则圆锥母线长与底面半径的比为 .
13.某校图书馆利用节假日面向社会开放.据统计,第一个月进馆500人次,进馆人次逐月增加,第三个月进馆720人次,设该图书馆第二个月、第三个月进馆人次的平均增长率为x,则可列方程为 .
14.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是 .
15.如图,直线AB,CD相交于点O,∠AOC=30°,圆P的半径为1cm,动点P在直线AB上从点O左侧且距离O点6cm处,以1cm/s的速度向右运动,当圆P与直线CD相切时,圆心P的运动时间为 s.
16.如图,在矩形ABCD中,点N为边BC上不与B、C重合的一个动点,过点N作MN⊥BC交AD于点M,交BD于点E,以MN为对称轴折叠矩形ABNM,点A、B的对应点分别是G,F,连接EF、DF,若AB=3,BC=4,当△DEF为直角三角形时,CN的长为 .
17.如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在x轴正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,那么经过第2022次旋转后,顶点D的坐标为 .
三.解答下列各题
18.解方程:
(1)4(2x﹣1)2﹣25=0;
(2)3x(x﹣1)=2﹣2x.
19.共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
(1)小沈从中随机抽取一张卡片是“共享服务”的概率是 ;
(2)小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)
20.已知关于x的一元二次方程(a﹣3)x2﹣4x+3=0有两个不等的实根.
(1)求a的取值范围;
(2)当a取最大整数值时,△ABC的三条边长均满足关于x的一元二次方程(a﹣3)x2﹣4x+3=0,求△ABC的周长.
21.如图,AB为⊙O的直径,射线AD交⊙O于点F,点C为劣弧的中点,过点C作CE⊥AD,垂足为E,连接AC.
(1)求证:CE是⊙O的切线;
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
22.某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时)与时间x(小时)成反比例函数关系缓慢减弱.
(1)这场沙尘暴的最高风速是 千米/小时,最高风速维持了 小时;
(2)当x≥20时,求出风速y(千米/小时)与时间x(小时)的函数关系式;
(3)在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,“危险时刻”共有 小时.
23.综合与实践
问题:如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为E,GF⊥CD,垂足为F.
证明与推断
(1)①四边形CEGF的形状是 ;②的值为 ;
【探究与证明】
(2)在图1的基础上,将正方形CEGF绕点C按顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
【拓展与运用】
(3)如图3,在(2)的条件下,正方形CEGF在旋转过程中,当B、E、F三点共线时,AG和GE的位置关系是 .
24.综合与探究
如图,在平面直角坐标系中,抛物线y=ax2+2x+c(a≠0)与x轴交于点A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.
(1)求抛物线的解析式;
(2)抛物线上C、D两点之间的距离是 ;
(3)点E是第一象限内抛物线上的动点,连接BE和CE,求△BCE面积的最大值;
(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
参考答案
一.选择题
1.垃圾分类一小步,低碳生活一大步,垃圾桶上常有以下四种垃圾分类标识的图案和文字说明,其中图案是中心对称图形的是( )
A.有害垃圾 B.厨余垃圾 C.其它垃圾 D.可回收物
【分析】把一个图形绕某一点旋转180°后与自身重合,那么这个图形就叫做中心对称图形.据此判断即可.
解:A.是中心对称图形,故本选项符合题意;
B.不是中心对称图形,故本选项不合题意;
C.不是中心对称图形,故本选项不合题意;
D.不是中心对称图形,故本选项不符合题意.
故选:A.
2.下列方程中是关于x的一元二次方程的是( )
A. B.ax2+bx+c=0
C.(x﹣1)(x﹣2)=0 D.3x2+2=x2+2(x﹣1)2
【分析】根据一元二次方程的定义解答,未知数的最高次数是2;二次项系数不为0;是整式方程;含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
解:A、是分式方程.故A错误;
B、当a=0时不是一元二次方程,故B错误;
C、是,一元二次方程,故C正确;
D、是一元一次方程.故D错误;
故选:C.
3.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
A.(3,3) B.(4,3) C.(3,1) D.(4,1)
【分析】利用位似图形的性质结合两图形的位似比进而得出C点坐标.
解:∵线段AB的两个端点坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,
∴端点C的横坐标和纵坐标都变为A点的一半,
∴端点C的坐标为:(3,3).
故选:A.
4.下列事件中,为必然事件的是( )
A.明天要下雨
B.太阳从东边升起
C.﹣2>﹣1
D.打开电视机,它正在播广告
【分析】根据必然事件的定义即可判断.
解:A.明天要下雨,是随机事件,故选项不符合题意;
B.太阳从东边升起,是必然事件,故选项符合题意;
C.﹣2>﹣1,是不可能事件,故选项不符合题意;
D.打开电视机,它正在播广告,是随机事件,故选项不符合题意;
故选:B.
5.如图,在△ABC 中,∠C=90°,BC=6,D,E 分别在 AB、AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
A. B.2 C.3 D.4
【分析】△ABC沿DE折叠,使点A落在点A′处,可得∠DEA=∠DEA′=90°,AE=A′E,所以,△ACB∽△AED,A′为CE的中点,所以,可运用相似三角形的性质求得.
解:∵△ABC沿DE折叠,使点A落在点A′处,
∴∠DEA=∠DEA′=90°,AE=A′E,
∴DE∥BC
∴△ACB∽△AED,
又A′为CE的中点,
∴AE=A′E=A′C=AC,
∴,
即,
∴ED=2.
故选:B.
6.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
【分析】设y=(k≠0),根据当x=2时,y=20,求出k,即可得出y与x的函数图象.
解:设y=(k≠0),
∵当x=2时,y=20,
∴k=40,
∴y=,
则y与x的函数图象大致是C,
故选:C.
7.将抛物线的图象向上平移2个单位后得到y=x2的图象,那么原图象的表达式是( )
A.y=(x﹣2)2 B.y=(x+2)2 C.y=x2+2 D.y=x2﹣2
【分析】直接根据“上加下减”的原则进行解答.
解:将抛物线y=x2的图象向下平移2个单位后得到原来的抛物线,那么原抛物线的表达式是:y=x2﹣2,
故选:D.
8.如图,小芳和爸爸正在散步,爸爸身高1.8米,他在地面上的影长为2.1米.若小芳身高只有1.2m,则她的影长为( )
A.1.2m B.1.4m C.1.6m D.1.8米
【分析】设小芳的影长为h,再根据同一时刻物高与影长成正比即可求出h的值.
解:设小芳的影长为h米,
∵同一时刻物高与影长成正比,
∴,
解得h=1.4.
故选:B.
9.已知点A(x1,y1),B(x2,y2)是反比例函数y=﹣的图象上的两点,若x1<0<x2,则下列结论正确的是( )
A.y1<0<y2 B.y2<0<y1 C.y1<y2<0 D.y2<y1<0
【分析】根据反比例函数图象上点的坐标特征得到y1=﹣,y2=﹣,然后利用x1<0<x2即可得到y1与y2的大小.
解:∵A(x1,y1),B(x2,y2)是反比例函数y=﹣的图象上的两点,
∴y1=﹣,y2=﹣,
∵x1<0<x2,
∴y2<0<y1.
故选:B.
10.如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图象给出下列结论:
①a+b+c=0;
②a﹣2b+c<0;
③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;
④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;
⑤a﹣b<m(am+b)(m为任意实数).
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【分析】①将(1,0)代入二次函数y=ax2+bx+c可对①进行判断;
②根据开口方向和与y轴的交点位置可得a>0,c<0,根据抛物线的对称轴方程得到﹣=﹣1,则可对②进行判断;
③利用二次函数的对称性可对③进行判断;
④因为抛物线开口向上,离对称轴越远,函数值越大,可对④进行判断;
⑤根据二次函数的性质,根据x=﹣1时y有最小值可对⑤进行判断.
解:①∵二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),
∴a+b+c=0,
故①正确;
②∵抛物线的对称轴为直线x=﹣=﹣1,
∴b=2a,
∵抛物线开口向上,与y轴交于负半轴,
∴a>0,c<0,
∴a﹣2b+c=c﹣3a<0,
故②正确;
③由对称得:抛物线与x轴的另一交点为(﹣3,0),
∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1,
故③正确;
④∵对称轴为直线x=﹣1,且开口向上,
∴离对称轴越近,y值越小,
∵|﹣4+1|=3,||﹣2+1|=1,|3+1|=4,
∵点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,
∴y2<y1<y3,
故④不正确;
⑤∵x=﹣1时,y有最小值,
∴a﹣b+c≤am2+bm+c(m为任意实数),
∴a﹣b≤m(am+b),
故⑤不正确.
所以正确的结论有①②③,共3个.
故选:C.
二.填空题
11.若一元二次方程的二次项系数为1,常数项为0,它的一个根为2,则该方程为 x2﹣2x=0 .
【分析】直接利用已知要求得出符合题意的方程.
解:由题意可得,该方程的一般形式为:x2﹣2x=0.
故答案为:x2﹣2x=0.
12.一个圆锥的侧面展开图是半圆,则圆锥母线长与底面半径的比为 2:1 .
【分析】根据圆锥的侧面展开扇形的周长等于圆锥的底面周长,分别设出圆锥的母线长和圆锥的底面半径,利用上述关系得到关系式求出两者的比值即可.
解:设圆锥的母线长为R,底面半径为r,
∵圆锥的侧面展开图是一个半圆,
∴圆锥的侧面展开扇形的弧长为:πR,
∵圆锥的侧面展开扇形的周长等于圆锥的底面周长,
∵πR=2πr,
∴R:r=2:1,
故答案为:2:1.
13.某校图书馆利用节假日面向社会开放.据统计,第一个月进馆500人次,进馆人次逐月增加,第三个月进馆720人次,设该图书馆第二个月、第三个月进馆人次的平均增长率为x,则可列方程为 500(1+x)2=720 .
【分析】利用第三个月进馆人次=第一个月进馆人次×(1+平均增长率)2,即可得出关于x的一元二次方程,此题得解.
解:依题意得:500(1+x)2=720.
故答案为:500(1+x)2=720.
14.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是 25° .
【分析】根据切线的性质求出∠OAC,结合∠C=40°求出∠AOC,根据等腰三角形性质求出∠B=∠BDO,根据三角形外角性质求出即可.
解:∵AC是⊙O的切线,
∴∠OAC=90°,
∵∠C=40°,
∴∠AOC=50°,
∵OB=OD,
∴∠ABD=∠BDO,
∵∠ABD+∠BDO=∠AOC,
∴∠ABD=25°,
故答案为:25°.
15.如图,直线AB,CD相交于点O,∠AOC=30°,圆P的半径为1cm,动点P在直线AB上从点O左侧且距离O点6cm处,以1cm/s的速度向右运动,当圆P与直线CD相切时,圆心P的运动时间为 4或8 s.
【分析】求得当⊙P位于点O的左边与CD相切时t的值和⊙P位于点O的右边与CD相切时t的值即可.
解:当点P在射线OA时⊙P与CD相切,如图,过P作PE⊥CD于E,
∴PE=1cm,
∵∠AOC=30°,
∴OP=2PE=2cm,
∴⊙P的圆心在直线AB上向右移动了(6﹣2)cm后与CD相切,
∴⊙P移动所用的时间==4(秒);
当点P在射线OB时⊙P与CD相切,如图,过P作PE⊥CD与F,
∴PF=1cm,
∵∠AOC=∠DOB=30°,
∴OP=2PF=2cm,
∴⊙P的圆心在直线AB上向右移动了(6+2)cm后与CD相切,
∴⊙P移动所用的时间==8(秒).
当⊙P的运动时间为4或8时,⊙P与直线CD相切.
故答案为:4或8.
16.如图,在矩形ABCD中,点N为边BC上不与B、C重合的一个动点,过点N作MN⊥BC交AD于点M,交BD于点E,以MN为对称轴折叠矩形ABNM,点A、B的对应点分别是G,F,连接EF、DF,若AB=3,BC=4,当△DEF为直角三角形时,CN的长为 或 .
【分析】根据△DEF为直角三角形时,可能出现三种情况,分别令不同的内角为直角,画出相应的图形,根据折叠的性质和相似三角形的性质进行解答即可.
解:∵矩形ABCD中,AB=3,BC=4,
∴BD==5,
由折叠得:BE=EF,BN=NF,∠EBF=∠EFB,∠BEN=∠FEN,
当△DEF为直角三角形时,
(1)当∠DEF=90°,则
∠BEN=∠FEN=45°,不合题意;
(2)当∠FED=90°时,如图所示:
∵∠EFN+∠DFC=90°,
∠DFC+∠CDF=90°,
∴∠EFN=∠CDF=∠EBN,
∵tan∠DBC===tan∠CDF=,
设CN=x,则BN=NF=4﹣x,
FC=x﹣(4﹣x)=2x﹣4,
∴,
解得:x=,
即CN=;
(3)当∠EDF=90°时,如图所示:
则△BDC∽△DFC,
∴CD2=BC•CF,
设CN=x,则BN=NF=4﹣x,
FC=(4﹣x)﹣x=4﹣2x,
∴32=4×(4﹣2x),
解得:x=,
即CN=,
综上所述,CN的长为或,
故答案为:或.
17.如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在x轴正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,那么经过第2022次旋转后,顶点D的坐标为 (,). .
【分析】如图,连接AD,BD.首先确定点D的坐标,再根据6次一个循环,由2022÷6=337,推出经过第2022次旋转后,顶点D的坐标与原来的坐标相同,由此即可解决问题.
解:如图,连接AD,BD,
在正六边形ABCDEF中,AB=1,AD=2,∠ABD=90°,
∴BD==,
在Rt△AOF中,AF=1,∠OAF=60°,
∴∠OFA=30°,
∴OA=AF=,
∴OB=OA+AB=,
∴D(,),
∵将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,
∴6次一个循环,
∵2022÷6=337,
∴经过第2022次旋转后,顶点D的坐标与应该不变,
∴经过第2022次旋转后,顶点D的坐标(,).
故答案为(,).
三.解答下列各题
18.解方程:
(1)4(2x﹣1)2﹣25=0;
(2)3x(x﹣1)=2﹣2x.
【分析】(1)将常数项移到方程的右边,再将二次项系数化为1,继而两边都加上一次项系数一半的平方配成完全平方式后,再开方即可得;
(2)先移项,再将左边利用提公因式法因式分解,继而可得两个关于x的一元一次方程,分别求解即可得出答案.
解:(1)∵4(2x﹣1)2﹣25=0,
∴4(2x﹣1)2=25,
∴(2x﹣1)2=,
∴2x﹣1=±,
解得x1=,x2=;
(2)∵3x(x﹣1)=2﹣2x,
∴3x(x﹣1)+2(x﹣1)=0,
∴(x﹣1)(3x+2)=0,
则x﹣1=0或3x+2=0,
解得x1=1,x2=﹣.
19.共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
(1)小沈从中随机抽取一张卡片是“共享服务”的概率是 ;
(2)小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)
【分析】(1)根据概率公式直接得出答案;
(2)根据题意先画树状图列出所有等可能的结果数,两张卡片恰好是“共享出行”和“共享知识”的结果数为2,根据概率公式求解可得.
解:(1)∵有共享出行、共享服务、共享物品、共享知识,共四张卡片,
∴小沈从中随机抽取一张卡片是“共享服务”的概率是,
故答案为:;
(2)画树状图如图:
共有12种等可能的结果数,其中两张卡片恰好是“共享出行”和“共享知识”的结果数为2,
∴抽到的两张卡片恰好是“共享出行”和“共享知识”的概率==.
20.已知关于x的一元二次方程(a﹣3)x2﹣4x+3=0有两个不等的实根.
(1)求a的取值范围;
(2)当a取最大整数值时,△ABC的三条边长均满足关于x的一元二次方程(a﹣3)x2﹣4x+3=0,求△ABC的周长.
【分析】(1)关于x的一元二次方程(a﹣3)x2﹣4x+3=0有两个不相等的实数根,可知二次项系数不为0且判别式大于0.
(2)在此范围内找出最大的整数,然后分四种情况讨论,求得三角形周长即可.
解:(1)∵关于x的一元二次方程(a﹣3)x2﹣4x+3=0有两个不相等的实数根,
∴,
解得a<且a≠3.
(2)由(1)得a的最大整数值为4;
∴x2﹣4x+3=0
解得:x1=1,x2=3.
∵△ABC的三条边长均满足关于x的一元二次方程(a﹣3)x2﹣4x+3=0,
∴①三边都为1,则△ABC的周长为3;
②三边都为3,则△ABC的周长为9;
③三边为1,1,3,因为1+1<3,此情况不存在;
④三边为1,3,3,则△ABC的周长为7.
21.如图,AB为⊙O的直径,射线AD交⊙O于点F,点C为劣弧的中点,过点C作CE⊥AD,垂足为E,连接AC.
(1)求证:CE是⊙O的切线;
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
【分析】(1)连接BF,证明BF∥CE,连接OC,证明OC⊥CE即可得到结论;
(2)连接OF,求出扇形FOC的面积即可得到阴影部分的面积.
解:(1)连接BF,OC,
∵AB是⊙O的直径,
∴∠AFB=90°,即BF⊥AD,
∵CE⊥AD,
∴BF∥CE,
连接OC,
∵点C为劣弧的中点,
∴OC⊥BF,
∵BF∥CE,
∴OC⊥CE,
∵OC是⊙O的半径,
∴CE是⊙O的切线;
(2)连接OF,CF,
∵OA=OC,∠BAC=30°,
∴∠BOC=60°,
∵点C为劣弧的中点,
∴,
∴∠FOC=∠BOC=60°,
∵OF=OC,
∴∠OCF=∠COB,
∴CF∥AB,
∴S△ACF=S△COF,
∴阴影部分的面积=S扇形COF,
∵AB=4,
∴FO=OC=OB=2,
∴S扇形FOC=,
即阴影部分的面积为:.
22.某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时)与时间x(小时)成反比例函数关系缓慢减弱.
(1)这场沙尘暴的最高风速是 32 千米/小时,最高风速维持了 10 小时;
(2)当x≥20时,求出风速y(千米/小时)与时间x(小时)的函数关系式;
(3)在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,“危险时刻”共有 59.5 小时.
【分析】(1)由速度=增加幅度×时间可得4时风速为8千米/时,10时达到最高风速,为32千米/时,与x轴平行的一段风速不变,最高风速维持时间为20﹣10=10小时;
(2)设y=,将(20,32)代入,利用待定系数法即可求解;
(3)由于4时风速为8千米/时,而4小时后,风速变为平均每小时增加4千米,所以4.5时风速为10千米/时,再将y=10代入(2)中所求函数解析式,求出x的值,再减去4.5,即可求解.
解:(1)0~4时,风速平均每小时增加2千米,所以4时风速为8千米/时;
4~10时,风速变为平均每小时增加4千米,10时达到最高风速,为8+6×4=32千米/时,
10~20时,风速不变,最高风速维持时间为20﹣10=10小时;
故答案为:32,10;
(2)设y=,
将(20,32)代入,得32=,
解得k=640.
所以当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系为y=;
(3)∵4时风速为8千米/时,而4小时后,风速变为平均每小时增加4千米,
∴4.5时风速为10千米/时,
将y=10代入y=,
得10=,解得x=64,
64﹣4.5=59.5(小时).
故在沙尘暴整个过程中,“危险时刻”共有 59.5小时.
故答案为:59.5.
23.综合与实践
问题:如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为E,GF⊥CD,垂足为F.
证明与推断
(1)①四边形CEGF的形状是 正方形 ;②的值为 ;
【探究与证明】
(2)在图1的基础上,将正方形CEGF绕点C按顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
【拓展与运用】
(3)如图3,在(2)的条件下,正方形CEGF在旋转过程中,当B、E、F三点共线时,AG和GE的位置关系是 AG⊥GE .
【分析】(1)根据正方形的判定和性质解决问题即可;
(2)结论:AG=BE.证明△ACG∽△BCE,可得=;
(3)结论:AG⊥GE,证明∠AGE=∠AGF﹣∠EGF=180°﹣90°=90°,可得结论.
解:(1)①正方形;②.
理由:如图1中,∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形,
∵AC=BC,CG=EC,
∴AG=AC﹣CG=(BC﹣EC)=BE,
∴=.
故答案为:正方形,;
(2)结论:AG=BE,
理由:如图2中,连接CC.由旋转可得∠BCE=∠AGG=α,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∴△ABC为等腰直角三角形,
∴,
由①得四边形GECF是正方形,
∴∠GEC=∠ECF=90°,GE=EC,
∴△EGC为等腰直角三角形.
∴=,
∴=,
∴△ACG∽△BCE,
∴=,
∴线段AG与BE之间的数量关系为AG=BE;
(3)如图3中,连接CG,
∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°.
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°.
∴∠AGF=∠AGC+∠CGF=135°+45°=180°,
∴点A,G,F三点共线,
∴∠AGE=∠AGF﹣∠EGF=180°﹣90°=90°,
∴AG⊥GE,
故答案为:AG⊥GE.
24.综合与探究
如图,在平面直角坐标系中,抛物线y=ax2+2x+c(a≠0)与x轴交于点A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.
(1)求抛物线的解析式;
(2)抛物线上C、D两点之间的距离是 2 ;
(3)点E是第一象限内抛物线上的动点,连接BE和CE,求△BCE面积的最大值;
(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
【分析】(1)先由题意得出A,B的坐标,再用待定系数法求出解析式即可;
(2)根据两点的距离公式即可求出CD的长度;
(3)先设出E的坐标,然后将△BCE的面积表示出来,求出最大值即可;
(4)根据对角线的情况分三种讨论,再由矩形的性质求出点Q的坐标.
解:(1)∵OA=1,
∴A(﹣1,0),
又∵对称轴为x=2,
∴B(5,0),
将A,B代入解析式得:
,
解得,
∴,自变量x为全体实数;
(2)由(1)得:C(0,),D(2,),
∴CD=,
故答案为2;
(3)∵B(5,0),C(0,),
∴直线BC的解析式为:,
设E(x,),且0<x<5,
作EF∥y轴交BC于点F,
则F(x,),
∴EF=﹣()=,
∴,
当x=时,S△BCE有最大值为;
(4)设P(2,y),Q(m,n),
由(1)知B(5,0),C(0,),
若BC为矩形的对角线,
由中点坐标公式得:,
解得:,
又∵∠BPC=90°,
∴PC2+PB2=BC2,
即:,
解得y=4或y=﹣,
∴n=或n=4,
∴Q(3,)或Q(3,4),
若BP为矩形的对角线,
由中点坐标公式得,
解得,
又∵∠BCP=90°,
BC2+CP2=BP2,
即:,
解得y=,
∴Q(7,4),
若BQ为矩形的对角线,
由中点坐标公式得,
解得:,
又∵∠BCQ=90°,
∴BC2+CQ2=BQ2,
即:,
解得n=,
∴Q(﹣3,﹣),
综上,点Q的坐标为(3,)或(3,4),或(7,4)或(﹣3,﹣).
相关试卷
这是一份黑龙江省齐齐哈尔市铁锋区2021-2022学年九年级上学期期中数学【试卷+答案】,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2021-2022学年黑龙江省齐齐哈尔市铁锋区七年级(下)期末数学试卷(Word解析版),共19页。试卷主要包含了0分,【答案】B,【答案】C,【答案】A等内容,欢迎下载使用。
这是一份2021-2022学年黑龙江省齐齐哈尔市铁锋区七年级(下)期中数学试卷(Word解析版),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。










