湖北省十堰市2020-2021学年八年级上学期期末考试数学试题（word版 含答案）

这是一份湖北省十堰市2020-2021学年八年级上学期期末考试数学试题（word版 含答案），共8页。

十堰市2020～2021学年度上学期期末考试
八年级数学试题
注意事项：
1．本卷共有4页，共有25小题，满分120分，考试时限120分钟．
2．答题前，考生先将自己的姓名、准考证号填写在试卷和答题卡指定的位置，并认真核对条形码上的准考证号和姓名，在答题卡规定的位置贴好条形码．
3．考生必须保持答题卡的整洁，考试结束后，请将本试卷和答题卡一并上交．
一、选择题（本题有10个小题，每小题3分，共30分）
下面每小题给出的四个选项中，只有一个是正确的，请把正确选项的字母填涂在答题卡中相应的格子内．
1．下列各组数可能是一个三角形的边长的是（　　）
A．4，4，9 B．2，6，8 C．3，4，5 D．1，2，3

2．下列运算正确的是（　　）
A．a•a5＝a5 B．(—a3)2 ＝a 6 C．a8÷a2 ＝a4 D．a3 +a3 ＝a6
3．下列等式中，从左到右的变形中是因式分解的是（　　）
A．9x2—6x+1＝(3x—1)2 B．x2﹣4x+1＝x(x—4)+1
C．3m(m—n)＝3m2—3mn D．x+3y＝(x+y)+2y
4．如果把分式中的x， y都扩大3倍，那么分式的值 （ ）
A．扩大3倍 B．不变 C．缩小3倍 D．扩大9倍

5．如图所示，AB = AC ，要说明△ADC≌△AEB，需添加的条件不能是（　　）
A．∠B ＝∠C B． AD = AE
（第5题）
C．∠ADC＝∠AEB D． DC = BE
（第6题）
（第7题）






6．如图，△ABC中，∠C＝70°，若沿图中虚线截去∠C，则∠1+∠2＝（　　）
A．360° B．250° C．180° D．140°

7．如图是台球桌面示意图，四个角是四个入球孔，小明按图中方向击球（球可以多次反弹），则球最后落入的球袋是（　　）
A．1号袋 B．2号袋 C．3号袋 D．4号袋

8．甲做360个零件与乙做480个零件所用的时间相等，已知两人每天共做140个零件，若设甲每天做x个零件，则可列方程 （ ）
A． B．
C． D．
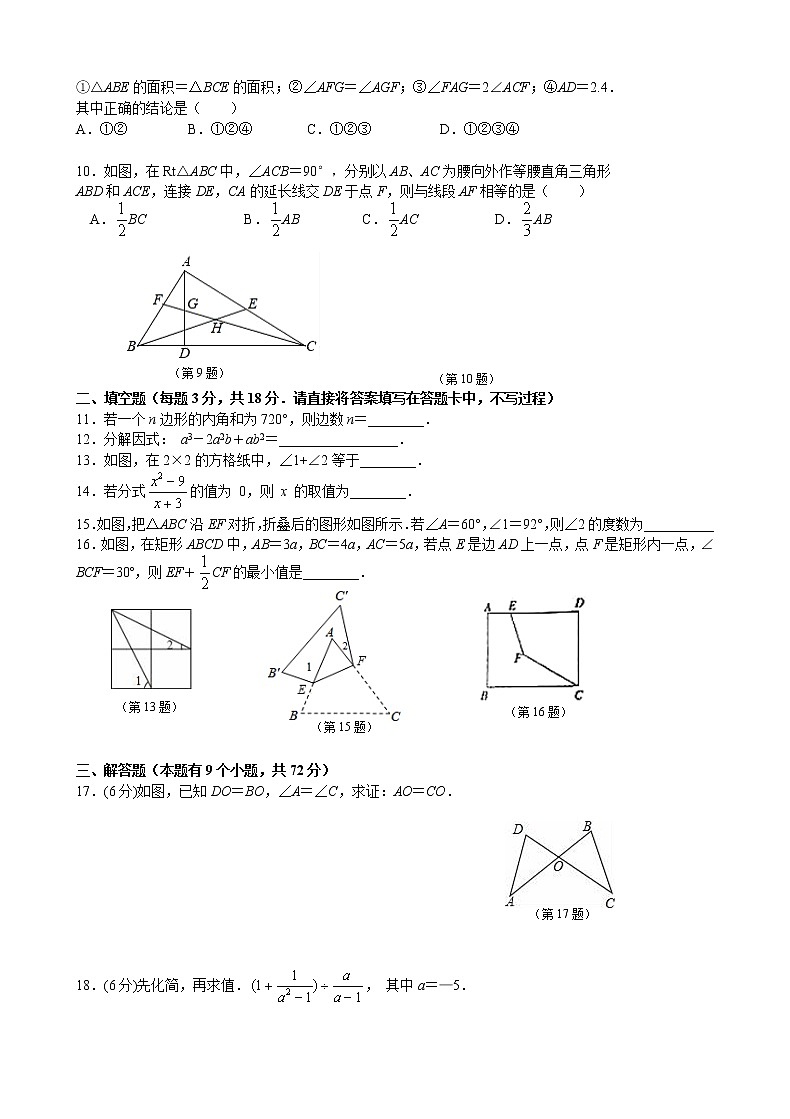
9．如图，在△ABC中，∠BAC＝90°，AB＝6，AC＝8，BC＝10，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，下面结论：
①△ABE的面积＝△BCE的面积；②∠AFG＝∠AGF；③∠FAG＝2∠ACF；④AD＝2.4．
其中正确的结论是（　　）
A．①② B．①②④ C．①②③ D．①②③④

10．如图，在Rt△ABC中，∠ACB＝90°，分别以AB、AC为腰向外作等腰直角三角形
ABD和ACE，连接DE，CA的延长线交DE于点F，则与线段AF相等的是（　　）
A．BC B．AB C．AC D．AB
（第10题）
（第9题）







二、填空题（每题3分，共18分．请直接将答案填写在答题卡中，不写过程）
11．若一个n边形的内角和为720°，则边数n＝________．
12．分解因式： a3－2a2b＋ab2＝_________________．
13．如图，在2×2的方格纸中，∠1+∠2等于________．
14．若分式的值为 0，则 x 的取值为________．
15．如图，把△ABC沿EF对折，折叠后的图形如图所示．若∠A＝60°，∠1＝92°，则∠2的度数为__________
（第15题）
16．如图，在矩形ABCD中，AB＝3a，BC＝4a，AC＝5a，若点E是边AD上一点，点F是矩形内一点，∠BCF＝30º，则EF＋CF的最小值是________．
（第16题）
（第13题）








三、解答题（本题有9个小题，共72分）
17．(6分)如图，已知DO＝BO，∠A＝∠C，求证：AO＝CO．
（第17题）








18．(6分)先化简，再求值．， 其中a＝—5．

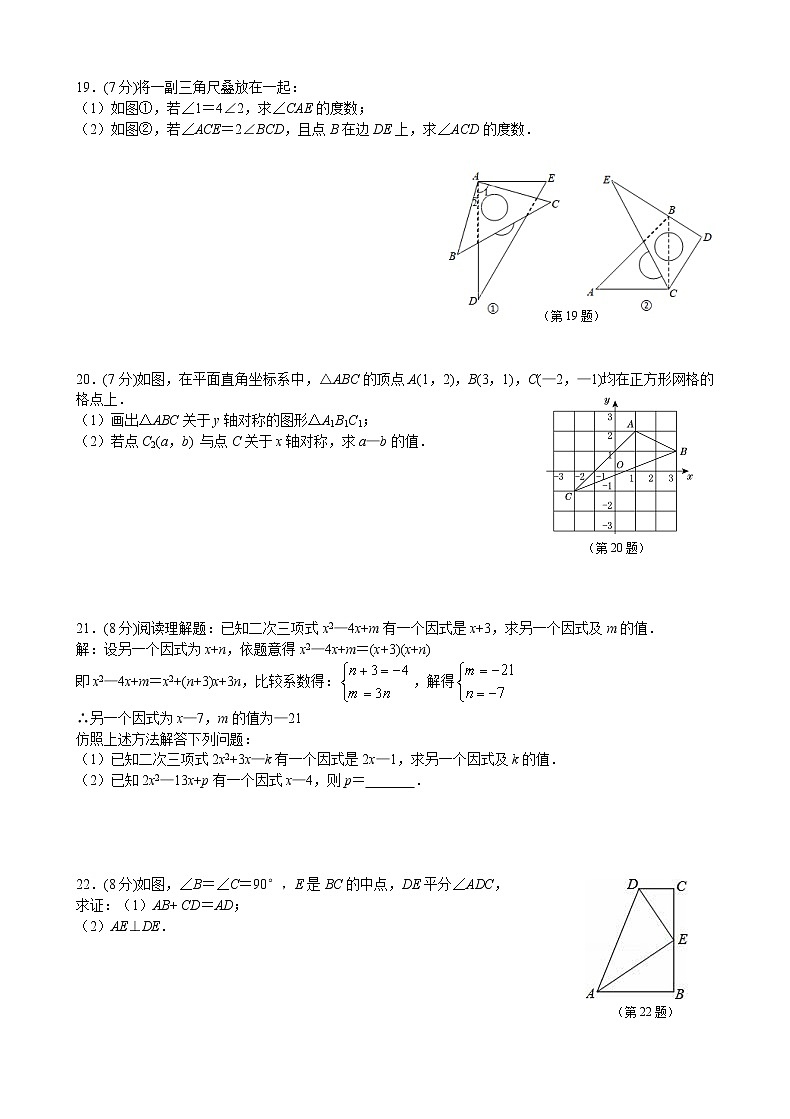
19．(7分)将一副三角尺叠放在一起：
（1）如图①，若∠1＝4∠2，求∠CAE的度数；
（2）如图②，若∠ACE＝2∠BCD，且点B在边DE上，求∠ACD的度数．

（第19题）










（第20题）
20．(7分)如图，在平面直角坐标系中，△ABC的顶点A(1，2)，B(3，1)，C(—2，—1)均在正方形网格的格点上．
（1）画出△ABC关于y轴对称的图形△A1B1C1；
（2）若点C2(a，b) 与点C关于x轴对称，求a—b的值．








21．(8分)阅读理解题：已知二次三项式x2—4x+m有一个因式是x+3，求另一个因式及m的值．
解：设另一个因式为x+n，依题意得x2—4x+m＝(x+3)(x+n)
即x2—4x+m＝x2+(n+3)x+3n，比较系数得：，解得
∴另一个因式为x—7，m的值为—21
仿照上述方法解答下列问题：
（1）已知二次三项式2x2+3x—k有一个因式是2x—1，求另一个因式及k的值．
（2）已知2x2—13x+p有一个因式x—4，则p＝　 　．




（第22题）
22．(8分)如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC，
求证：（1）AB+ CD＝AD；
（2）AE⊥DE．





23．(8分)某单位在疫情期间用8000元购进A、B两种口罩共3400个，已知购买A种口罩的费用是购买B种口罩费用的3倍，且A种口罩的单价是B种口罩单价的1.25倍；
（1）求A，B两种口罩的单价各是多少元？
（2）若计划用不超过15000元的资金再次购进A、B两种口罩共7000个，已知A、B两种口罩的进价不变，求A种口罩最多能购进多少个？







24．(10分)如图，等边△ABC中，BM是ÐABC内部的一条射线，且∠ABM ＜30º，点A关于BM的对称点为D，连接AD，BD，CD，其中AD、CD的延长线分别交射线BM于点E，P．
（1）依题意补全图形；
（第24题）
（2）若ÐABM =a，求ÐBDC 的大小（用含a的式子表示）；
（3）用等式表示线段PB，PC与PE之间的数量关系，并证明．









25．(12分)如图1已知点A，B分别在坐标轴上，点C(3，－3)，CA⊥BA于点A，且
BA＝CA，CA，CB分别交坐标轴于D，E．
（1）填空：点B的坐标是___________；
（2）如图2，连接DE，过点C作CH⊥CA于C，交x轴于点H，
求证：ÐADB=ÐCDE；
（3）如图3，点F(6，0)，点P在第一象限，连PF，过P作PM⊥PF交y轴于点M，在
PM上截取PN＝PF，连PO，过P作ÐOPG =45°交BN于G，
（第25题图3）
求证：点G是BN中点．
（第25题图2）
（第25题图1）












2020-2021学年第一学期期末考试
八年级数学试题参考答案

一、选择题:1．C；2．B；3．A；4．B；5．D；6．B；7．B；8．A；9．C；10．A．
二、填空题:11．6； 12．a(a－b)2； 13．90º ； 14．3； 15．28º； 16．3a．
三、解答题：2(m＋2)( m－2)
17．(6分)
（第17题）
证明：在△ADO和△CBO中
∵
∴△ADO≌△CBO……………………………………………………5分
∴AO＝CO ……………………………………………………………6分
18．(6分)
解：＝………………………………2分
＝ …………………………………………………………………4分
当a＝－5时，＝………………………………………………6分
（第19题）
19．(7分)
解：（1）设∠2＝a，则∠1＝4a
由∠1＋∠2＝90º，得a＋4a＝90º
解得，a＝18º
∴∠2＝18º……………………………………………2分
∵∠1＋∠2＝∠1＋∠CAE＝90º
∴∠CAE＝∠2＝18º…………………………………3分
（2）设∠BCD＝β，则∠ACE＝2β，∠BCE＝60º －β
由∠ACE＋∠BCE＝90º，得2β＋60º －β＝90º
（第20题）
C1
A1
B1
解得，β＝30º…………………………………………6分
∴∠ACD＝∠ACB＋∠BCD＝120º…………………7分

20．(7分)
解：（1）如图…………………………………………3分
（2）∵点C2(a，b) 与点C关于x轴对称
∴a＝－2，b＝1………………………………………5分
∴a－b＝－3 …………………………………………7分

21．(8分)
解：(1)设另一个因式为x＋m，则2x2+3x—k＝(2x—1)( x＋m)
即2x2+3x—k＝2x2＋(2m—1)x—m……………………………………………………………………2分

比较系数得：，解得 …………………………………………………………4分
∴另一个因式为x＋2，k的值为2． ………………………………………………………………5分

(2)20……………………………………………………………………………………………………8分


（第22题）
F
22．(8分)
解法①证明：(1)延长DE交AB的延长线城于点F．
∵∠ABC＝∠C＝90º，∴DC∥AB
∴∠CDE＝∠F
∵点E是BC中点， ∴CE＝BE
∴△CDE≌△BEF(AAS)
∴CD＝BF…………………………………………………………………………………………2分
∵DE平分∠ADC， ∴∠ADE＝∠CDE
∴∠ADE＝∠F……………………………………………………………………………………4分
∴AD＝AF＝AB＋BF＝AB＋CD…………………………………………………………………5分
(2)由(1)可证△CDE≌△BEF
∴DE＝FE…………………………………………………………………………………………6分
由(1)知AD＝AF …………………………………………………………………………………7分
∴AE⊥DE．………………………………………………………………………………………8分

解法②证明：(1)过点E作EM⊥AD于M．
（第22题）
M
∵∠ADE＝∠CDE，EM⊥AD，DC⊥CB
∴EC＝EM……………………………………………………………1分
∴Rt△CDE≌Rt△MDE(HL)， ∴DC＝DM………………………3分
∵EC＝EB， ∴EM＝EB
∵∠AME＝∠B＝90º
∴Rt△ABE≌Rt△AME(HL)
∴AB＝AM……………………………………………………………4分
∴AD＝AM＋DM＝AB＋CD…………………………………………5分
(2) 由(1)可证Rt△ABE≌Rt△AME(HL)
∴∠DAE＝∠BAE＝∠DAB
∵∠ADE＝∠CDE＝∠ADC，∴∠DAE＋∠ADE＝(∠DAB＋∠ADC)＝90º ……………………7分
∴AE⊥DE．…………………………………………………………………………………………………8分
【注】本题证法较多，只要正确，可参照给分．
23．(8分)
解：(1) 设B种口罩的单价为x元/个，则A种口罩单价为1.25x元/个．
依题意列方程得，………………………………………………………3分
解得，x＝2………………………………………………………………………………………4分
经检验，x＝2是方程的根，且符合题意．
1.25x＝2.5
答：A种口罩单价为2.5元/个，B种口罩单价为2元/个．…………………………………5分

(2) 设购进A口罩m个，则购进B口罩(7000﹣m)个，
依题意，得：2.5m+2(7000﹣m)≤15000，……………………………………………………7分
（第24题图1）
解得：m≤2000．
答：A种口罩最多能购进2000个．………………………………8分
24．(10分)
（1）如图所示；……………………………………………………2分
（2）解： ∵点A与点D关于BM对称，
∴BM是AD的垂直平分线， ∴BA=BD．
∵∠ABM=a， ∴∠ABD=2∠ABM=2a．………………………3分
∵△ABC是等边三角形， ∴BA=BC=BD，∠ABC=60°，
∴∠DBC=∠ABC－∠ABD =60°－2a，……………………………4分
∴∠BDC=∠DCB=(180°－∠DBC)=60°+a．……………………6分
（第24题图2）
（3）结论：PB=PC+2PE．证明如下：……………………………7分
如图2，在射线PD上截取PF使PF=PB，连接BF．
∵BA=BD，∠ABD=2a，∴∠BDA=∠BAD=90°－a．
∵∠BDC=60°+a，∴∠PDE=180－(∠BDA+∠BDC) =30°．
∵∠DEP=90°， ∴PD=2PE．……………………………………8分
∵∠BPF=∠DPE=90°－∠PDE=60°，PF=PB，∴△BPF是等边三角形，
∴∠BPF=∠BFP=60°．
∵∠BDC=∠DCB，∴∠BDP=∠BCF．
∴△BFC≌△BPD(AAS)， ∴CF=PD=2PE，……………………9分
∴PB= PC+BF=PC+2PE．…………………………………………10分

25．(12分)
G
（第25题图2）
F
(1) B(0，6) ………………………………………………………………3分
(2)过点C作CG⊥x轴于G，CF⊥y轴于F，则CF∥AO．
∵∠BOA＝∠CGA＝90º
∴∠ABO＋∠BAO＝∠BAO＋∠CAG＝90º
∴∠ABO＝∠CAG
又∵AB＝AC
∴△ABO≌△CAG(AAS)
∴AO＝CG＝3
∵CF＝3
∴AO＝CF………………………………………………………………4分
∵CF∥AO
∴∠DAO＝∠DCF，∠AOD＝∠CFD
∴△AOD≌△CFD(ASA)
∴AD＝CD………………………………………………………………5分
∵∠ABO＝∠CAG，∠BAD＝∠ACH＝90º，AB＝AC
∴△BAD≌△ACH(ASA)
∴AD＝CH，∠ADB＝∠AHC
∴CD＝CH………………………………………………………………6分
L
（第25题图3）
K
又∵∠DCE＝∠HCE＝45º
∴△DCE≌△HCE(SAS)
∴∠CDE＝∠CHE
∴∠ADB＝∠CDE………………………………………………………7分

(3)过点O作OK⊥OP交PG延长线于K，连BK，过点P作PL⊥NF于L．
则△OPK是等腰直角三角形，
∠OPF＝∠OPL＋45º，∠GPN＝∠OPL＝45º－∠MPO
∵∠KOB＋∠BOP＝∠FOP＋∠BOP＝90º
∴∠KOB＝∠FOP
∵FD＝FB，OB＝OF＝6
∴△OKB≌△OPF(SAS)
∴KB＝PF＝PN，……………………………………………………9分
∠OKB＝45º＋∠GKB＝∠OPF＝∠OPL＋45º
∴∠GKB＝∠OPL＝∠GPN ………………………………………10分
又∵∠KGB＝∠PGN ………………………………………………11分
∴△KBG≌△PNG(SAS
∴BG＝NG
即点G为BN的中点． ……………………………………………12分