2019-2020学年四川省绵阳市江油市九年级（上）期末数学试卷

这是一份2019-2020学年四川省绵阳市江油市九年级（上）期末数学试卷，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
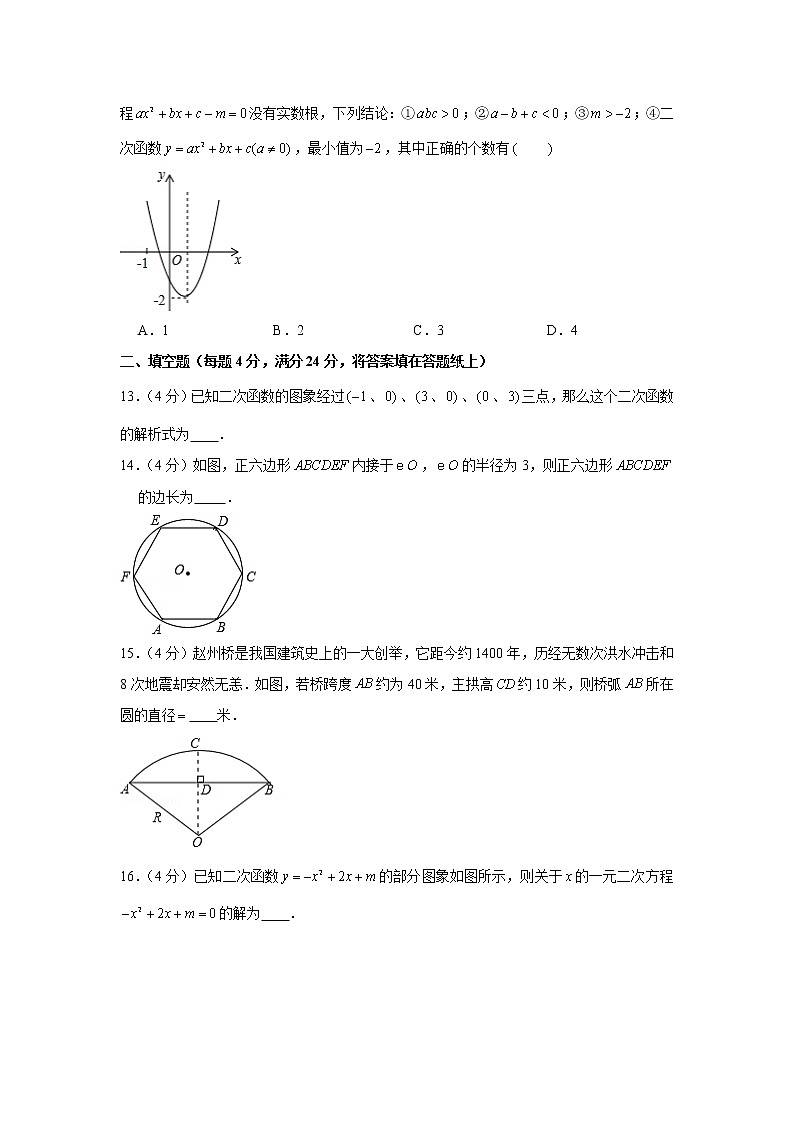
2019-2020学年四川省绵阳市江油市九年级（上）期末数学试卷一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（3分）下列事件是必然事件的是　　A．抛掷枚硬币四次，有两次正面朝上 B．打开电视频道，正在播放《篮球比赛》 C．射击运动员射击一次，命中十环 D．方程必有实数根2．（3分）下列图形中既是轴对称图形，又是中心对称图形的是　　A． B． C． D．3．（3分）用配方法解方程的配方过程正确的是　　A．将原方程配方 B．将原方程配方 C．将原方程配方 D．将原方程配方4．（3分）一个不透明的布袋里装有3个红球，2个黑球，若干个白球；从布袋中随机摸出一个球，摸出的球是红球的概率是，袋中白球共有　　A．1个 B．2个 C．3个 D．4个5．（3分）如图，是的直径，若，则　　A． B． C． D．6．（3分）在，，0，1，2这五个数中任取两数，，则二次函数的顶点在坐标轴上的概率为　　A． B． C． D．7．（3分）一种药品原价每盒25元，经过两次降价后每盒16元，设两次降价的百分率都为，则满足等式　　A． B． C． D．8．（3分）已知与关于原点对称，则的值为　　A． B． C． D．59．（3分）如图，从一块直径为的圆形纸片上，剪出一个圆心角为的扇形，使点，，都在圆周上，将剪下的扇形围成一个圆锥的侧面，则这个圆锥的底面圆的半径是　　A． B． C． D．10．（3分）如图，在中，，，，为的内切圆，点是斜边的中点，则的长是　　A． B．2 C．3 D．11．（3分）当时，函数的最小值为1，则的值为　　A．1 B．2 C．1或2 D．0或312．（3分）已知二次函数的图象如图所示，并且关于的一元二次方程没有实数根，下列结论：①；②；③；④二次函数，最小值为，其中正确的个数有　　A．1 B．2 C．3 D．4二、填空题（每题4分，满分24分，将答案填在答题纸上）13．（4分）已知二次函数的图象经过、、、、、三点，那么这个二次函数的解析式为　　．14．（4分）如图，正六边形内接于，的半径为3，则正六边形的边长为　 　．15．（4分）赵州桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙．如图，若桥跨度约为40米，主拱高约10米，则桥弧所在圆的直径　　米．16．（4分）已知二次函数的部分图象如图所示，则关于的一元二次方程的解为　　．17．（4分）把一副三角板如图1放置，其中，，，斜边，把三角板绕点顺时针旋转得到三角形（如图，此时与交于点，则线段的长度为　　．18．（4分）在平面直角坐标系内，以原点为圆心，1为半径作圆，点在直线上运动，过点作该圆的一条切线，切点为，则的最小值为　　．三、解答题（本大题共7小题，共90分.解答应写出文字说明、证明过程或演算步骤.）19．（12分）（1）解方程：．（2）如图，在平面直角坐标系中，点，点，点①以点为中心，把逆时针旋转，画出旋转后的图形，②求点经过的路径的长（结果保留．20．（12分）甲、乙两校分别有一男一女共4名教师报名到农村中学支教．（1）若从甲、乙两校报名的教师中分别随机选1名，则所选的2名教师性别相同的概率是　　．（2）若从报名的4名教师中随机选2名，用列表或画树状图的方法求出这2名教师来自同一所学校的概率．21．（12分）如图，四边形是的内接四边形，对角线是的直径，，是的内心，．（1）求半径的长．（2）求证：．22．（12分）关于的方程有两个不相等的实数根．（1）求的取值范围．（2）是否存在实数，使方程的两个实数根的倒数和等于2？若存在，求出的值；若不存在，说明理由．23．（14分）如图，在平面直角坐标系中，点为内任一点，连接、、，将绕着点顺时针旋转得到△，连接．（1）求点的坐标；（2）当与满足什么条件时，的值最小，并求出此最小值；24．（14分）如图，在中，，的平分线交于点，过点作的垂线交于点，是的外接圆．（1）求证：是的切线；（2）过点作，垂足为，若，，求长．25．（14分）如图，已知一条直线过点，且与抛物线交于，两点，其中点的横坐标是．（1）求这条直线的函数关系式及点的坐标．（2）在轴上是否存在点，使得是直角三角形？若存在，求出点的坐标，若不存在，请说明理由．（3）过线段上一点，作轴，交抛物线于点，点在第一象限，点，当点的横坐标为何值时，的长度最大？最大值是多少？
2019-2020学年四川省绵阳市江油市九年级（上）期末数学试卷参考答案与试题解析一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（3分）下列事件是必然事件的是　　A．抛掷枚硬币四次，有两次正面朝上 B．打开电视频道，正在播放《篮球比赛》 C．射击运动员射击一次，命中十环 D．方程必有实数根【解答】解：、抛掷枚硬币四次，有两次正面朝上是随机事件，故此选项不合题意；、打开电视频道，正在播放《篮球比赛》是随机事件，故此选项不合题意；、射击运动员射击一次，命中十环是随机事件，故此选项不符合题意；、方程必有实数根是必然事件，故此选项符合题意；故选：．2．（3分）下列图形中既是轴对称图形，又是中心对称图形的是　　A． B． C． D．【解答】解：、是轴对称图形，不是中心对称图形；、不是轴对称图形，是中心对称图形；、是轴对称图形，是中心对称图形；、是轴对称图形，不是中心对称图形；故选：．3．（3分）用配方法解方程的配方过程正确的是　　A．将原方程配方 B．将原方程配方 C．将原方程配方 D．将原方程配方【解答】解：由移项，得，等式两边同时加上一次项系数一半的平方，得，．故选：．4．（3分）一个不透明的布袋里装有3个红球，2个黑球，若干个白球；从布袋中随机摸出一个球，摸出的球是红球的概率是，袋中白球共有　　A．1个 B．2个 C．3个 D．4个【解答】解：设白球有个，根据题意，得：，解得：，即袋中白球有2个，故选：．5．（3分）如图，是的直径，若，则　　A． B． C． D．【解答】解：是的直径，，，，．故选：．6．（3分）在，，0，1，2这五个数中任取两数，，则二次函数的顶点在坐标轴上的概率为　　A． B． C． D．【解答】解：画树状图得：，，0，1，2这五个数中任取两数，，一共有20种等可能的结果，其中取到0的结果有8种，顶点在坐标轴上的概率为．故选：．7．（3分）一种药品原价每盒25元，经过两次降价后每盒16元，设两次降价的百分率都为，则满足等式　　A． B． C． D．【解答】解：第一次降价后的价格为：；第二次降价后的价格为：；两次降价后的价格为16元，．故选：．8．（3分）已知与关于原点对称，则的值为　　A． B． C． D．5【解答】解：与关于原点对称，，，则．故选：．9．（3分）如图，从一块直径为的圆形纸片上，剪出一个圆心角为的扇形，使点，，都在圆周上，将剪下的扇形围成一个圆锥的侧面，则这个圆锥的底面圆的半径是　　A． B． C． D．【解答】解：，圆锥的底面圆的半径．故选：．10．（3分）如图，在中，，，，为的内切圆，点是斜边的中点，则的长是　　A． B．2 C．3 D．【解答】解：如图，在中，，，，，设与的三边的切点为、、，连接、、，得正方形设，则，，，解得，，点是斜边的中点，，，在中，根据勾股定理，得．故选：．11．（3分）当时，函数的最小值为1，则的值为　　A．1 B．2 C．1或2 D．0或3【解答】解：当时，有，解得：，．当时，函数有最小值1，或，或，故选：．12．（3分）已知二次函数的图象如图所示，并且关于的一元二次方程没有实数根，下列结论：①；②；③；④二次函数，最小值为，其中正确的个数有　　A．1 B．2 C．3 D．4【解答】解：①对称轴在轴右侧，则，而，故正确，符合题意；②当时，，故原选项错误，不符合题意；③关于的一元二次方程没有实数根，即与没有交点，故，原选项错误，不符合题意；④从图象看二次函数的最小值为，故符合题意；故选：．二、填空题（每题4分，满分24分，将答案填在答题纸上）13．（4分）已知二次函数的图象经过、、、、、三点，那么这个二次函数的解析式为　　．【解答】解：设抛物线解析式为，把代入得，解得，所以抛物线解析式为，即．故答案为．14．（4分）如图，正六边形内接于，的半径为3，则正六边形的边长为　3　．【解答】解：正六边形内接于，的半径为3，而正六边形可以分成六个边长的正三角形，正多边形的半径即为正三角形的边长，正三角形的边长为3，正六边形的边长为3，故答案为：315．（4分）赵州桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙．如图，若桥跨度约为40米，主拱高约10米，则桥弧所在圆的直径　50　米．【解答】解：根据垂径定理，得米．设圆的半径是，根据勾股定理，得，解得（米，的直径为50米．故答案为50．16．（4分）已知二次函数的部分图象如图所示，则关于的一元二次方程的解为　或　．【解答】解：依题意得二次函数的对称轴为，与轴的一个交点为，抛物线与轴的另一个交点横坐标为，交点坐标为当或时，函数值，即，关于的一元二次方程的解为或．故答案为：或．17．（4分）把一副三角板如图1放置，其中，，，斜边，把三角板绕点顺时针旋转得到三角形（如图，此时与交于点，则线段的长度为　　．【解答】解：如图，于交于点，，，，斜边，，，，，将三角板绕点顺时针旋转得到三角形，，，，，，，故答案为：．18．（4分）在平面直角坐标系内，以原点为圆心，1为半径作圆，点在直线上运动，过点作该圆的一条切线，切点为，则的最小值为　　．【解答】解：如图，设直线与轴交于点，与轴交于点，作于，当时，，则，，当时，，解得，则，，，，连接，如图，为的切线，，，当的值最小时，的值最小，而的最小值为的长，的最小值，故答案为：．三、解答题（本大题共7小题，共90分.解答应写出文字说明、证明过程或演算步骤.）19．（12分）（1）解方程：．（2）如图，在平面直角坐标系中，点，点，点①以点为中心，把逆时针旋转，画出旋转后的图形，②求点经过的路径的长（结果保留．【解答】解：（1），，，；（2）①如图所示，△即为所求；②，旋转角为，点经过的路径．20．（12分）甲、乙两校分别有一男一女共4名教师报名到农村中学支教．（1）若从甲、乙两校报名的教师中分别随机选1名，则所选的2名教师性别相同的概率是　　．（2）若从报名的4名教师中随机选2名，用列表或画树状图的方法求出这2名教师来自同一所学校的概率．【解答】解：（1）根据题意画图如下：共有4种情况，其中所选的2名教师性别相同的有2种，则所选的2名教师性别相同的概率是；故答案为：； （2）将甲、乙两校报名的教师分别记为甲1、甲2、乙1、乙2（注表示男教师，2表示女教师），树状图如图所示：所以．21．（12分）如图，四边形是的内接四边形，对角线是的直径，，是的内心，．（1）求半径的长．（2）求证：．【解答】解：（1）是的直径，，又，，，，的半径为；（2）连接，是的内心．，，，，，，即．22．（12分）关于的方程有两个不相等的实数根．（1）求的取值范围．（2）是否存在实数，使方程的两个实数根的倒数和等于2？若存在，求出的值；若不存在，说明理由．【解答】解：（1）关于的方程有两个不相等的实数根，解得且（2）假设存在实数，使方程两实数根的倒数和为2设方程的两根为、，，，即，解得不存在实数使方程两根的倒数和为223．（14分）如图，在平面直角坐标系中，点为内任一点，连接、、，将绕着点顺时针旋转得到△，连接．（1）求点的坐标；（2）当与满足什么条件时，的值最小，并求出此最小值；【解答】解：（1），，，将绕着点顺时针旋转得到△，，，（2）连接．由旋转可得，是等边三角形，，，，当0、、、四点共线时，的值最小，即时，的值最小，此时，．24．（14分）如图，在中，，的平分线交于点，过点作的垂线交于点，是的外接圆．（1）求证：是的切线；（2）过点作，垂足为，若，，求长．【解答】解：（1）证明：连接，平分，又，，又即．，即是的切线；（2）连接，平分，、，，，，，，，解得：，．25．（14分）如图，已知一条直线过点，且与抛物线交于，两点，其中点的横坐标是．（1）求这条直线的函数关系式及点的坐标．（2）在轴上是否存在点，使得是直角三角形？若存在，求出点的坐标，若不存在，请说明理由．（3）过线段上一点，作轴，交抛物线于点，点在第一象限，点，当点的横坐标为何值时，的长度最大？最大值是多少？【解答】解：（1）点是直线与抛物线的交点，且横坐标为，，点的坐标为，设直线的函数关系式为，将，代入得，解得，直线，直线与抛物线相交，，解得：或，当时，，点的坐标为； （2）如图1，连接，，由，可求得．设点，同理可得，，①若，则，即，解得：；②若，则，即，解得：或；③若，则，即，解得：；点的坐标为，，，， （3）设，如图2，设与轴交于点，在中，由勾股定理得，又点与点纵坐标相同，，，点的横坐标为，，，当，又，取到最大值18，当的横坐标为6时，的长度的最大值是18．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2021/12/7 16:12:18；用户：初中数学2；邮箱：jse033@xyh.com；学号：39024123