第25讲 锐角三角函数-讲义2021-2022学年人教版九年级数学下册学案

第二十八章  锐角三角函数

第25讲  锐角三角函数

知识导航

1．正弦、余弦、正切的概念及表示方法．

2．特殊角的三角函数值．

【板块一】求锐角三角函数值

方法技巧

1．结合图形，理解并牢记三角函数的定义．

2．数形结合法熟记特殊角的三角函数值．

3．求一个角的三角函数值，一般利用已有的或构造的直角三角形，也可以利用等角转化等，结合三角函数定义求解．

题型一  紧扣定义求三角函数值

【例1】已知锐角α满足tanα＝，求sinα的值．

【解析】在Rt△ABC中，∠C＝90°，∠A＝α，∵tanα＝，∴设BC＝x，AC＝2x，∴AB＝＝＝，∴．

【点评】由于三角函数的定义是基于直角三角形，所以要画出符合题意的直角三角形，结合勾股定理和三角函教的定义求解．

【例2】如图，在正方形ABCD中，点M为AD的中点，点E为AB上一点，且BE＝3AE，求cos∠ECM的值．

【解析】首先确定△EMC为直角三角形，设AE＝x，则BE＝3x，AM＝MD＝2x，CD＝4x．∴，又∠A＝∠D＝90°，∴△AEM∽△DMC，可得∠EMC＝90°，由勾股定理可求CM＝2x，CE＝5x，在Rt△CEM 中，cos∠ECM＝．

题型二  等角转换求三角函数值

【例3】如图，半径为3的⊙A经过原点O和点C(0，2)，点B是y轴左侧⊙A优弧上一点，求tan∠OBC的值．

【解析】作直径CD，在Rt△OCD中．CD＝6．OC＝2．∴OD＝＝4，tan∠CDO＝＝,由圆周角定理得∠OBC＝∠CDO，则tan∠OBC＝

【点评】在圆中经常利用同弧或等弧所对的圆周角相等进行角的转换，用直径所对的圆周角去构造直角三角形．

题型三  构造直角求三角函数值

【例4】如图，在Rt△BAD中，tan∠B＝，延长斜边BD到点C，使DC＝BD，连接AC，求tan∠CAD的值．

【解析】要求tan∠CAD，必须将∠CAD放在直角三角形中，考虑∠BAD＝90°，故过点D作DE∥AB交AC 于点E．则∠ADE＝90°，且有△CDE∽△CBA可利用，由tan∠B＝，设AD＝5x，AB＝3x，而，∴DE＝x，∴tan∠CAD＝．

【点评】求一个角的三角函数值，必须将所求的角放在直角三角形中．

题型四  等比转化求三角函数值

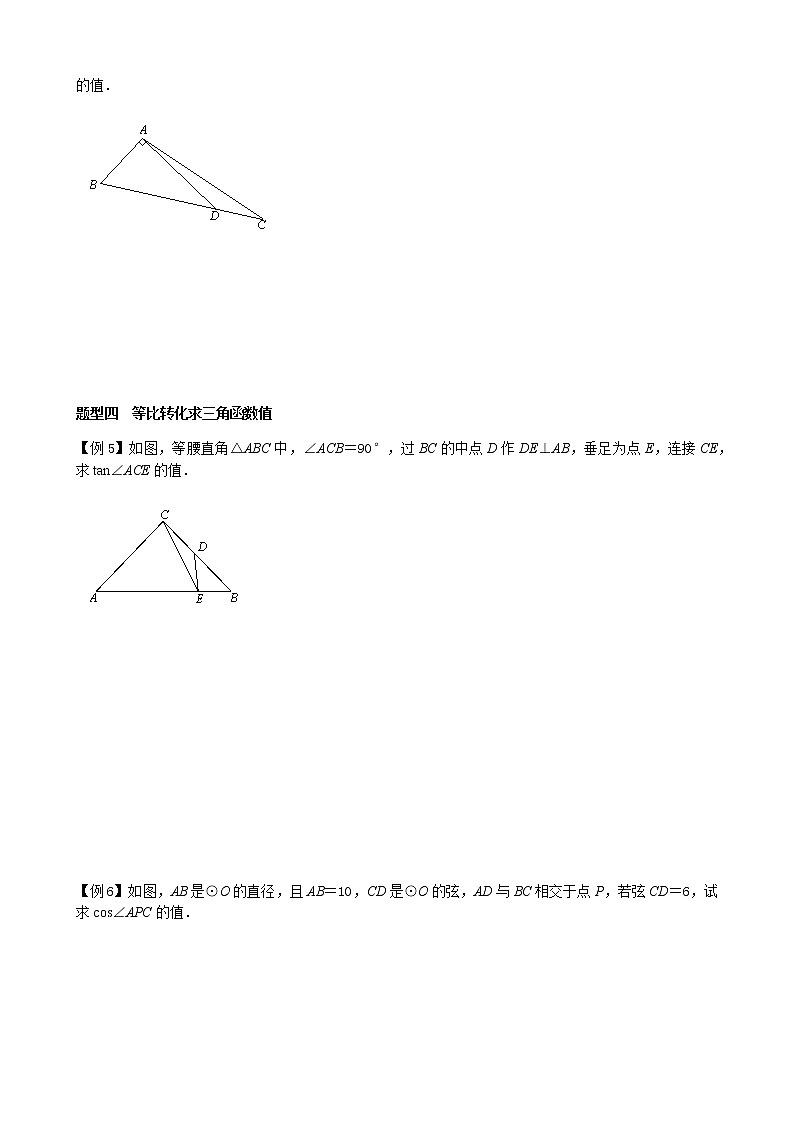
【例5】如图，等腰直角△ABC中，∠ACB＝90°，过BC的中点D作DE⊥AB，垂足为点E，连接CE，求tan∠ACE的值．

【解析】过点E作EH⊥AC于点H，易证AH＝HE，∴tan∠ACE＝，设BE＝x，则BD＝CD＝x，∴BC＝2x，AB＝4x，∴AE＝AB－BE＝3x，∴tan∠ACE＝＝3．

【例6】如图，AB是⊙O的直径，且AB＝10，CD是⊙O的弦，AD与BC相交于点P，若弦CD＝6，试求cos∠APC的值．

【解析】连接AC，∵AB是⊙O的直径，∴∠ACP＝90°，∴cos∠APC＝，又易证△PCD∽△PAB,∴，∴cos∠APC＝．

【点评】在直角三角形中，锐角的三角函数值等于两边的比值，当这个比值无法直接求解时，可利用相似三角形对应线段成比例进行转化．

题型五  利用特殊角求三角函数值

【例7】利用45°角的正切，求tan22．5°的值，方法如下：

解：构造Rt△ABC，其中∠C＝90°，∠B＝45°，如图，延长CB到点D，使BD＝AB，连接AD，则∠D＝∠ABC＝22．5°，设AC＝a，AB＝BD＝a，∴CD＝(1＋)a，∴tan22．5°＝tan∠D＝＝－1．

请你依照此法求tan15°的值．

【解析】构造如图所示的∠A＝15°的直角三角形，∠C＝90°，并过点B作∠ABD＝15°交AC于点D，则∠BDC＝30°，设BC＝x，则BD＝AD＝2x，CD＝x，∴AC＝(2＋)x，∴tan15°＝＝＝2－．

针对练习1

1．如图，△ABC的顶点是正方形网格的格点，则sinA＝     ．

2．在Rt△ABC中，∠C＝90°，sinA＝，则tanB＝     ．

3．如图，将边长为2的正方形ABCD沿 EF 和ED折叠，使得点B，C两点折叠后重合于点G，则tan∠FEG＝     ．

4．如图，直线MN与⊙O相切于点M，ME＝EF，EF∥MN，则cos∠E＝    ．

5．如图，在△ABC中，∠C＝90°，BC＝1，AC＝4，求tan的值．

解：AB＝＝7．延长CA到点D，使AD＝AB＝7，则CD＝7＋4，∴tan＝tan∠D＝＝7－4．

6．如图，AC为⊙O的直径，△ABD内接于⊙O，BD交AC于点F，过点B的切线BE∥AD交AC的延长线于点E，若CF＝2，AF＝8，求sin∠E的值．

解：连接OB，CD，∵CF＝2，AF＝8，∴AC＝10．∴OB＝5．易证CD⊥AD，OB⊥AD，∴OB∥CD，∴△BOF∽△DCF．∴．CD＝．sin∠E＝sin∠CAD＝＝．

7．将一副三角尺(Rt△ABC与Rt△BDC)按如图所示摆放在一起，连接AD，试求∠ADB的正切值．

解：过点A作AM⊥DB交DB的延长线于点M，易证∠MBA＝45°，∴设AM＝BM＝x，则AB＝x．∴BC＝x，BD＝x．∴tan∠ADB＝＝＝＝．

8．如图，在△ABC中，BC＝4，AC＝6，AB＝5，求tan∠BAC·tan∠CBA的值．

解：过点C作CH⊥AB于点H，延长BA到点D，使AD＝AC，延长AB到点E，使BE＝BC，设AH＝x，则BH＝5－x，∴42－(5－x)2＝62－x2，∴x＝．∴BH＝，CH＝＝，∴tan∠BAC＝tan∠D＝＝＝．tan∠CBA＝tan∠E＝＝＝，∴tan∠BAC·tan∠CBA＝×＝．

方法技巧：

深刻理解三角函数的定义，画出符合题意的示意图，充分运用数形结合的思想解题．

▶题型一 利用已知三角函数，求其他角的三角函数值

【例1】同学们，在我们进入高中以后，将会学到三角函数公式：sin2α＝2sinα·cosα，则当锐角a的正切值为时，sin2a＝     ．

【解析】如图，在Rt△ABC中．∠C＝90°，∠A＝α，由tanα＝＝，设BC＝1，AC＝2，则AB＝．sinα＝＝＝，cosα＝＝，由公式sin2α＝2sinα·cosα＝2××＝．

【点评】紧扣定义，运用公式解题．

▶题型二　利用已知三角函数，求线段长

【例2】如图，点D是△ABC的边AC上一点，BD＝8，sin∠CBD＝，AE⊥BC于点E，若CD＝2AD，求AE的长．

【解析】过点D作DF⊥BC于点F，则DF＝BD·sin∠CBD＝8×2＝6，由AE⊥ BC．DF⊥BC，∴DF∥AE．∴△CDF∽△CAE．∴＝＝．∴AE＝DF＝9．

【点评】因三角函数的本质是线段比，故与三角函数相关的计算常与相似三角形联系在一起．

▶题型三 利用已知三角函数，求线段比

【例3】如图，在Rt△ABC中，CD，CE分别为斜边AB上的高和中线，BC＝a，AC＝b(b＞a)，若tan

∠DCE＝，求的值．

【解析】易证△BCD∽△BAC，∴BC2＝BD·BA，又BA＝，∴BD＝，同理CD＝，∴DE＝BE－BD＝－＝，又∵谈∠DCE＝＝＝，∴a2＋ab－b2＝0，∴＝．

▶题型四　利用已知三角函数，求面积

【例4】如图，在四边形ABCD中，∠BAC＝90°，tan∠CAD＝，cos∠ACD＝，AC与BD交于点E，CD＝，BE＝2ED，求四边形ABCD的面积．

【解析】过点D作DF⊥ACC于点F，则AB∥DF．∴△ABE∽△FDE．∴＝＝＝2，设EF＝2a，AE＝4a．∴AF＝6a，在 Rt△AFD 中．tan∠FAD＝＝，∴DF＝3a，在Rt△CFD中，cos∠ACD＝＝．∴CF＝1，DF＝3a＝3，∴a＝1，AC＝7，AB＝2DF＝6，∴S四边形ABCD＝S△ABC＋S△AC＝AB·AC＋AC·DF＝×6×7＋×7×3＝．

针对练习2

1．在△ABC中，∠A为锐角，BC＝12．tanA＝．∠B＝30°，则AB＝    ．

2．如图，点E是正方形ABCD的边CB的延长线上的一点，且tan∠DEC＝，则tan∠AED的值为    ．

3．已知△ABC中，AB＝10，AC＝2，∠B＝30°，则△ABC的面积为  或  ．

4．如图，在四边形ABCD中，BD是对角线，∠ABC＝90”，tan∠ABD＝，AB＝20，BC＝10，AD＝13，求CD的长．

解：分别过点A，C作AH⊥BD于点H，CG⊥BD于点G，∵tan∠ABD＝＝，∴设AH＝3x，BH＝4x，(3x)2＋(4x)2＝202，∴x＝4．∴AH＝12，BH＝16．∴HD＝＝5，BD＝21，易证∠BCG＝∠ABD，．．tan∠BCG＝＝，又BC＝10，∴BG＝6，CG＝8，∴DG＝BD－BG＝15，∴CD＝＝＝17．

5．如图，在△ABC中，AB＝BC＝5，tan∠ABC＝．边BC的重直平分线与AB的交点为点D．求的值．

解：过点D作DF⊥BC于点F，连接CD，则BD＝CD，BF＝CF＝，tan∠DBF＝＝．∴DF＝，在Rt△BFD中，BD＝＝，∴AD＝5－＝，∴＝．

6．如图，已知四边形ABCD的一组对边AD，BC的延长线相交于点E，∠ABC＝120°，cos∠ADC＝，CD＝5，AB＝12，ACDE的面积为6，求四边形ABCD的面积．

解：过点C作CF⊥AD于点F，过点A作AG⊥EB于点G，在Rt△ACDF中，cos∠ADC＝＝．又CD＝5，DF＝3，CF＝4，∵S△CDE＝ED·CF＝6，∴ED＝3，∴EF＝6，在Rt△BAG中，∠BAG＝30°，AB＝12，∴AG＝6．由△EFC∽△EAG，得＝，可求EG＝9，∴BE＝EG－BG＝9－6．∴S四边形ABCD＝S△ABE－S△CED＝(9－6)×6－6＝75－18．