

2019-2020学年福建省泉州市九年级(上)期末数学试卷
展开2019-2020学年福建省泉州市九年级(上)期末数学试卷
一、选择题:本题共10小题,每小题4分,共40分
1.(4分)要使二次根式有意义,字母x必须满足的条件是( )
A.x≥1 B.x>﹣1 C.x≥﹣1 D.x>1
2.(4分)若=,则=( )
A. B. C. D.
3.(4分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
4.(4分)某快递公司2017年“双十一”与2019年“双十一”期间完成投递的件数分别为8万件和11万件.设该快递公司这两年投递件数的年平均增长率为x,则下列方程正确的是( )
A.8(1+2x)=11 B.8(1+x)2=11
C.8(1+2x)2=11 D.8+8(1+x)+8(1+2x)2=11
5.(4分)如图,已知△ABC与△DEF位似,位似中心为点O,则AO:AD的值为( )
A.2:3 B.2:5 C.4:9 D.4:13
6.(4分)利用配方法解一元二次方程x2﹣6x+7=0时,将方程配方为(x﹣m)2=n,则m、n的值分别为( )
A.m=9,n=2 B.m=﹣3,n=﹣2 C.m=3,n=0 D.m=3,n=2
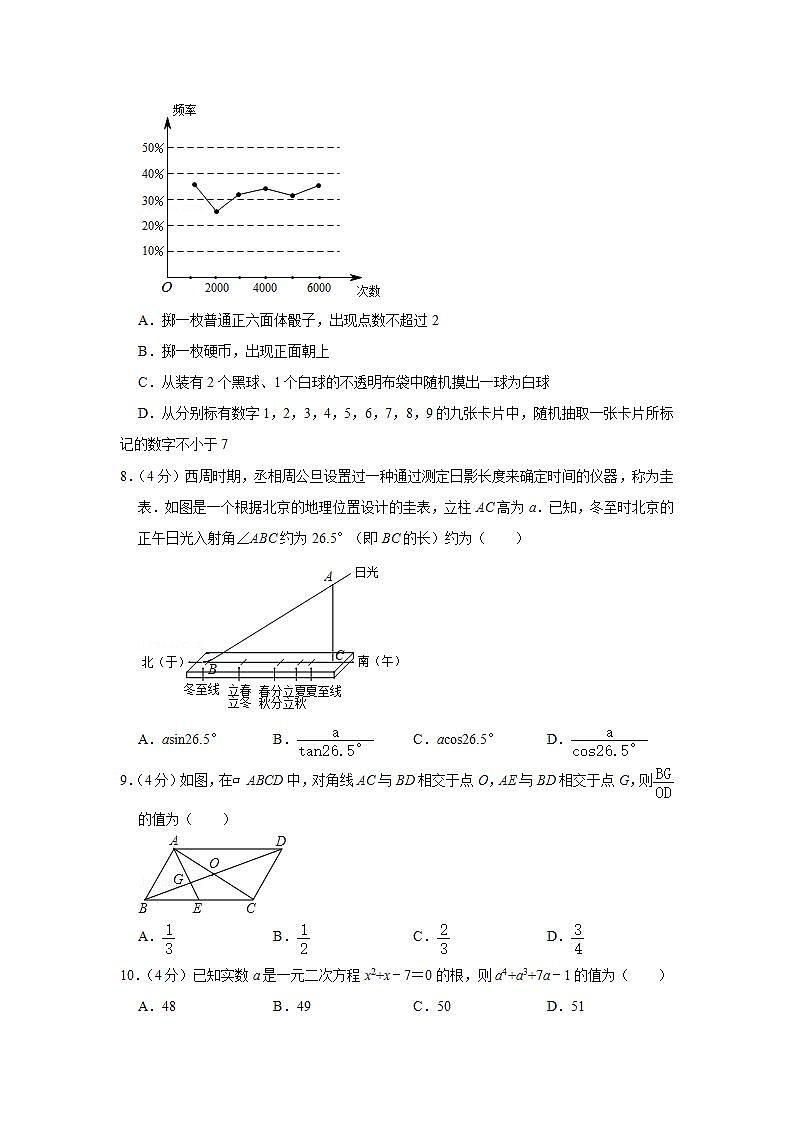
7.(4分)如图为某一试验结果的频率随机试验次数变化趋势图,则下列试验中不符合该图的是( )
A.掷一枚普通正六面体骰子,出现点数不超过2
B.掷一枚硬币,出现正面朝上
C.从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球
D.从分别标有数字1,2,3,4,5,6,7,8,9的九张卡片中,随机抽取一张卡片所标记的数字不小于7
8.(4分)西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°(即BC的长)约为( )
A.asin26.5° B. C.acos26.5° D.
9.(4分)如图,在▱ABCD中,对角线AC与BD相交于点O,AE与BD相交于点G,则的值为( )
A. B. C. D.
10.(4分)已知实数a是一元二次方程x2+x﹣7=0的根,则a4+a3+7a﹣1的值为( )
A.48 B.49 C.50 D.51
二、填空题:本题共6小题,每小题4分,共24分.
11.(4分)计算:+= .
12.(4分)一元二次方程x(x+1)﹣2(x+1)=0的根是 .
13.(4分)如图,河堤横断面迎水坡AC的坡度i=1:2,若BC=30米 米.
14.(4分)如图,在Rt△ABC中,∠C=90°,AB=6,M、N分别是AB与AC的中点 .
15.(4分)如图,在正方形网格中,△ABC的三个顶点都在格点上(∠CAB+∠ABC)= .
16.(4分)在正方形ABCD中,AB=8,点F在边AD上,连接AG并延长交CD于点E,若点E将CD分为1:3的两部分 .
三、解答题:本题共9小题,共86分.
17.(8分)计算:×+﹣2cos45°
18.(8分)已知关于x的一元二次方程ax2+bx+c=0的两根分别为x1、x2,有如下结论:x1+x2=﹣,x1x2=,试利用上述结论,解决问题:已知关于x的一元二次方程3x2﹣x﹣2019=0的两根分别为x1、x2,求(x1+2)(x2+2)的值.
19.(8分)某校有一块矩形绿地(数据如图所示,单位:m),现在其中修建一条道路(阴影所示),若所修建道路的面积为325m2,求x的值.
20.(8分)已知关于x的一元二次方程kx2+(k+1)x+1=0
(1)求证:这个方程一定有实根;
(2)若这个方程有一根为﹣3,试求k的值.
21.(8分)如图,在矩形ABCD中,AB=2AD.
(1)尺规作图:在线段CD上求一点E,使得∠AED=30°(保留作图痕迹,不写作法与证明);
(2)连接BE,若点F为边BE的中点,求证:∠EAF=∠EBC.
22.(10分)将一副直角三角尺按如图所示方式放置,点A、B、D在同一条直线上,EF∥AB,∠ACB=∠DEF=90°,∠A=45°,BD=3﹣3
23.(10分)某台机床生产铸件产品,按照生产标准,铸件产品评定等级、整改费用规定如下:
重量a(单位:kg,精确到0.1)
评定等级
整改费用
(单位:元/件)
a=30.0
特优品
/
29.9≤a≤30.1
优等品
/
29.8≤a≤30.2
合格品
/
a≤29.7
不合格品
50
a≥30.3
不合格品
30
注:在统计优等品个数时,将特优品计算在内;在统计合格品个数时(含特优品)计算在内.
现该机床生产20件产品,测量其重量,得到如下统计表:
重量a(单位:kg,精确到0.1)
a≤29.7
29.8
29.9
30.0
30.1
30.2
a≥30.3
件数
2
3
4
x
3
1
y
对照生产标准,发现这批铸件产品的合格率为80%.
(1)求x与y的值;
(2)根据客户要求,这批铸件产品的合格率不得低于90%,现决定从不合格产品中随机抽取两件进行整改
24.(12分)如图,在平面直角坐标系xOy中,直线l:y=﹣,点C是AB的中点,点E、F分别为线段AB、OB上的动点,使点B的对称点D恰好落在线段OA上(不与端点重合).连接OC分别交DE、DF于点M、N
(1)求tan∠ABO的值;
(2)试判断DE与FM的位置关系,并加以证明;
(3)若MD=MN,求点D的坐标.
25.(14分)如图,∠MBN=45°,点P为∠MBN内的一个动点,使得∠BPA=∠BPC=135°,分别交BM、BN于点A、C.
(1)求证:△CPB∽△BPA;
(2)连接AC,若AC⊥BC,试求;
(3)记AP=a,BP=b,CP=c,a≥2b,且a、b、c为整数,b,c的值.
2019-2020学年福建省泉州市九年级(上)期末数学试卷
参考答案与试题解析
一、选择题:本题共10小题,每小题4分,共40分
1.(4分)要使二次根式有意义,字母x必须满足的条件是( )
A.x≥1 B.x>﹣1 C.x≥﹣1 D.x>1
【解答】解:根据二次根式的意义,被开方数x+1≥0.
故选:C.
2.(4分)若=,则=( )
A. B. C. D.
【解答】解:=1+
∵=
∴=
把=代入=
故选:C.
3.(4分)下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【解答】解:A、=,故本选项错误;
B、=2;
C、=,故本选项错误;
D、=3.
故选:B.
4.(4分)某快递公司2017年“双十一”与2019年“双十一”期间完成投递的件数分别为8万件和11万件.设该快递公司这两年投递件数的年平均增长率为x,则下列方程正确的是( )
A.8(1+2x)=11 B.8(1+x)2=11
C.8(1+2x)2=11 D.8+8(1+x)+8(1+2x)2=11
【解答】解:设该快递公司这两年投递总件数的年平均增长率为x,
根据题意,得:8(1+x)4=11,
故选:B.
5.(4分)如图,已知△ABC与△DEF位似,位似中心为点O,则AO:AD的值为( )
A.2:3 B.2:5 C.4:9 D.4:13
【解答】解:∵△ABC与△DEF位似,位似中心为点O,
∴=,AC∥DF,
∴==,
∴=.
故选:B.
6.(4分)利用配方法解一元二次方程x2﹣6x+7=0时,将方程配方为(x﹣m)2=n,则m、n的值分别为( )
A.m=9,n=2 B.m=﹣3,n=﹣2 C.m=3,n=0 D.m=3,n=2
【解答】解:x2﹣6x+4=0,
x2﹣5x=﹣7,
x2﹣3x+9=﹣7+7,
(x﹣3)2=7,
则m=3,n=2.
故选:D.
7.(4分)如图为某一试验结果的频率随机试验次数变化趋势图,则下列试验中不符合该图的是( )
A.掷一枚普通正六面体骰子,出现点数不超过2
B.掷一枚硬币,出现正面朝上
C.从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球
D.从分别标有数字1,2,3,4,5,6,7,8,9的九张卡片中,随机抽取一张卡片所标记的数字不小于7
【解答】解:根据实验频率可以估计该事件发生的概率为,
掷一枚普通正六面体骰子,出现点数不超过2的概率为=;
掷一枚硬币,出现正面朝上的概率为;
从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球的概率为=;
从标有数字1,7,3,4,4,6,7,3,9的九张卡片中=,因此选项D不符合题意;
故选:B.
8.(4分)西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°(即BC的长)约为( )
A.asin26.5° B. C.acos26.5° D.
【解答】解:由题意可得,
立柱根部与圭表的冬至线的距离为:,
故选:B.
9.(4分)如图,在▱ABCD中,对角线AC与BD相交于点O,AE与BD相交于点G,则的值为( )
A. B. C. D.
【解答】解:∵点E是BC的中点,
∴BC=2BE,
∵四边形ABCD是平行四边形,
∴OB=OD,AD=BC=2BE,
∴△BEG∽△DAG,
∴==,
∴DG=2BG,
∴BD=6BG,OD=OB=,
∴=;
故选:C.
10.(4分)已知实数a是一元二次方程x2+x﹣7=0的根,则a4+a3+7a﹣1的值为( )
A.48 B.49 C.50 D.51
【解答】解:∵a是一元二次方程x2+x﹣7=2的一个根,
a2+a﹣7=4
∴a2+a=7,
∴a4+a3+7a﹣6=a2(a2+a)+2a﹣1=7a8+7a﹣1=49﹣7=48,
故选:A.
二、填空题:本题共6小题,每小题4分,共24分.
11.(4分)计算:+= 5 .
【解答】解:原式=4+=5,
故答案为:6.
12.(4分)一元二次方程x(x+1)﹣2(x+1)=0的根是 x=﹣1或x=2 .
【解答】解:∵x(x+1)﹣2(x+7)=0,
∴(x+1)(x﹣3)=0,
则x+1=2或x﹣2=0,
解得x=﹣7或x=2,
故答案为:x=﹣1或x=5.
13.(4分)如图,河堤横断面迎水坡AC的坡度i=1:2,若BC=30米 15 米.
【解答】解:∵迎水坡AC的坡度i=1:2,
∴=,即=,
解得,AB=15,
故答案为:15.
14.(4分)如图,在Rt△ABC中,∠C=90°,AB=6,M、N分别是AB与AC的中点 .
【解答】解:在Rt△ABC中,∠C=90°,
∴BC=AB=7,
∵M、N分别是AB与BC的中点,
∴MN=BC=,
故答案为:.
15.(4分)如图,在正方形网格中,△ABC的三个顶点都在格点上(∠CAB+∠ABC)= .
【解答】解:如图,∵∠DCB=∠CAB+∠ABC,
∵∠D=90°,
CD=BD==2,
∴△CDB是等腰直角三角形,
∴∠DCB=45°,
∴sin(∠CAB+∠ABC)=sin45°=,
故答案为:.
16.(4分)在正方形ABCD中,AB=8,点F在边AD上,连接AG并延长交CD于点E,若点E将CD分为1:3的两部分 0.4或 .
【解答】解:由题意可得,
AB=AD=CD=8,∠AHF=∠AHB=90°,
当DE:EC=3:4时,DE=6,
∵∠DAE+∠BAH=∠BAD=90°,∠ABF+∠BAH=90°,
∴∠DAE=∠ABF,
∵tan∠DAE=,
∴tan∠ABF=,
∴AF=6,
∵∠AHF=90°,tan∠HAF=,
∴AH=4.7,
∴HG=AH=4.8,
∴AG=4.6,
∵∠ADE=90°,AD=8,
∴AE=10,
∴GE=AE﹣AG=10﹣7.6=0.7;
当DE:EC=1:3时,DE=6,
同理可得,GE=;
故答案为:0.4或.
三、解答题:本题共9小题,共86分.
17.(8分)计算:×+﹣2cos45°
【解答】解:原式=+﹣2×
=4+﹣
=4.
18.(8分)已知关于x的一元二次方程ax2+bx+c=0的两根分别为x1、x2,有如下结论:x1+x2=﹣,x1x2=,试利用上述结论,解决问题:已知关于x的一元二次方程3x2﹣x﹣2019=0的两根分别为x1、x2,求(x1+2)(x2+2)的值.
【解答】解:由一元二次方程的根与系数的关系得到x1+x2=,x1•x6=﹣673,
(x1+2)(x2+2)
=x1•x4+2(x1+x4)+4
=﹣673+2×+4
=﹣668.
19.(8分)某校有一块矩形绿地(数据如图所示,单位:m),现在其中修建一条道路(阴影所示),若所修建道路的面积为325m2,求x的值.
【解答】解:由题意可得:(40﹣x)(30﹣x)=40×30﹣325
即(x﹣5)(x﹣65)=0,
解得:x4=5,x2=65,
经检验得:x=65不合题意,舍去,
答:x的值为2;
20.(8分)已知关于x的一元二次方程kx2+(k+1)x+1=0
(1)求证:这个方程一定有实根;
(2)若这个方程有一根为﹣3,试求k的值.
【解答】(1)证明:根据题意得k≠0
∵Δ=(k+1)4﹣4k=(k﹣1)3≥0,
∴这个方程一定有实根;
(2)解:把x=﹣3代入一元二次方程kx7+(k+1)x+1=3得9k﹣3(k+5)+1=0,
解得k=.
21.(8分)如图,在矩形ABCD中,AB=2AD.
(1)尺规作图:在线段CD上求一点E,使得∠AED=30°(保留作图痕迹,不写作法与证明);
(2)连接BE,若点F为边BE的中点,求证:∠EAF=∠EBC.
【解答】解:(1)如图,点E即为所求.
(2)∵AE=AB,BF=EF,
∴∠EAF=∠FAB,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠FAB+∠EBA=90°,∠EBA+∠EBC=90°,
∴∠FAB=∠EBC,
∴∠EAF=∠EBC.
22.(10分)将一副直角三角尺按如图所示方式放置,点A、B、D在同一条直线上,EF∥AB,∠ACB=∠DEF=90°,∠A=45°,BD=3﹣3
【解答】解:如图,作CH⊥AB于H.
∵AC=CB,∠ACB=90°,
∴AH=HB,
∴CH=AH=HB,设CH=AH=BH=x,
∵EF∥AD,
∴∠CDH=∠F=30°,
∴CD=2x,DH=x,
∵BD=4﹣3,
∴x﹣x=3,
∴x=5,
∴EF=AB=6,
∴DF==4,
∴CF=DF﹣CD=4﹣2.
23.(10分)某台机床生产铸件产品,按照生产标准,铸件产品评定等级、整改费用规定如下:
重量a(单位:kg,精确到0.1)
评定等级
整改费用
(单位:元/件)
a=30.0
特优品
/
29.9≤a≤30.1
优等品
/
29.8≤a≤30.2
合格品
/
a≤29.7
不合格品
50
a≥30.3
不合格品
30
注:在统计优等品个数时,将特优品计算在内;在统计合格品个数时(含特优品)计算在内.
现该机床生产20件产品,测量其重量,得到如下统计表:
重量a(单位:kg,精确到0.1)
a≤29.7
29.8
29.9
30.0
30.1
30.2
a≥30.3
件数
2
3
4
x
3
1
y
对照生产标准,发现这批铸件产品的合格率为80%.
(1)求x与y的值;
(2)根据客户要求,这批铸件产品的合格率不得低于90%,现决定从不合格产品中随机抽取两件进行整改
【解答】解:(1)合格的件数:20×80%=16件,不合格:20﹣16=4件,
∵a≤29.7的有8件,a≥30.3的有y件,
∴y=4﹣8=2,
∴x=20﹣2﹣8﹣4﹣3﹣6﹣y=5件,
答:x、y的值分别为5,6;
(2)原来不合格的有4个,即a≤29.7的有6件,
现从任意选择两个进行整改,用列表法表示所有可能出现的结果为:
(注:a≤29.7的有2件,记作A6、A2,a≥30.3的有3件,记作B1、B2
共有12中等可能出现的情况,其中选两个都是B的最省钱,
∴P(费用最低)==;
24.(12分)如图,在平面直角坐标系xOy中,直线l:y=﹣,点C是AB的中点,点E、F分别为线段AB、OB上的动点,使点B的对称点D恰好落在线段OA上(不与端点重合).连接OC分别交DE、DF于点M、N
(1)求tan∠ABO的值;
(2)试判断DE与FM的位置关系,并加以证明;
(3)若MD=MN,求点D的坐标.
【解答】解:(1)直线l:y=﹣x+2与x轴、A两点,
则点A、B的坐标分别为:(0、(3;
tan∠ABO===tanα;
(2)DE与FM的位置关系为相互垂直,理由:
点C是AB的中点,
则∠COB=∠CBO=∠EDF=α,∠ONF=∠DNM,
∴∠DMN=∠DFO,
∴O、F、M、D四点共圆,
∴∠DMF+∠DOF=180°,
∴∠DOF=90°,即:DE⊥FM;
解法二:∵∠NDM=∠NOF,∠DNM=∠ONF,
∴△DNM∽△ONF,
∴=,∠DMN=∠OFN,
∴=,
∵∠OND=∠FNM,
∴△OND∽△FNM,
∴∠DON=∠NFM,
∴∠MDN+∠NFM=∠NOF+∠DON=90°,
∴∠DMF=90°,
∴DE⊥FM.
(3)MD=MN,
∴∠MDN=∠MND=α,
而∠COB=α,∠DNM=∠ONF=α,
即△ONF为以ON为底,底角为α的等腰三角形,
则tan∠NFO===tanβ(证明见备注);
设OF=m,则DF=FB=3﹣m,
cos∠DFO=cosβ=,
解得:m=,
OD7=DF2﹣OF2=(5﹣m)2﹣m2=;
则OD=,
故点D(0,).
备注:如下图,
过点N作HN⊥OF于点H,tanα=,作FM⊥ON于点M,
设FN=OF=7a,则FM=4a,
同理可得:NH=,
sin∠NFO===sinβ.
25.(14分)如图,∠MBN=45°,点P为∠MBN内的一个动点,使得∠BPA=∠BPC=135°,分别交BM、BN于点A、C.
(1)求证:△CPB∽△BPA;
(2)连接AC,若AC⊥BC,试求;
(3)记AP=a,BP=b,CP=c,a≥2b,且a、b、c为整数,b,c的值.
【解答】(1)证明:∵∠BPA=135°,
∴∠ABP+∠BAP=180°﹣135°=45°,
∵∠ABP+∠CBP=∠MBN=45°,
∴∠ABP+∠BAP=∠ABP+∠CBP,
∴∠BAP=∠CBP,
∵∠BPA=∠BPC,
∴△CPB∽△BPA;
(2)解:∵AC⊥BC,∠MBN=45°,
∴△ACB是等腰直角三角形,
∴AB=BC,
∵△CPB∽△BPA,
∴====,
设PC=a,
则BP=a,AP=4a,
∵∠APC=360°﹣135°﹣135°=90°,
∴AC===a,
∴==;
(3)解:∵△CPB∽△BPA,
∴=,
即=≥2,
∴b2=ac,c≤,
∴a+b﹣c≥2b+b﹣=b,
∴b≤20,
∴b≤8,
∵a、b、c为正整数,
∴当b=8时,ac=64,
解得:a=16,c=3或a=﹣4,
当b=7时,a=14;与=矛盾,
当b<7时,c<0(b<7时,只能得到没有正整数解,
∴a,b,c的值为16,5,4.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/12/13 10:26:59;用户:初中数学3;邮箱:jse034@xyh.com;学号:39024124
2023-2024学年福建省泉州市鲤城区九年级(上)期末数学试卷(含解析): 这是一份2023-2024学年福建省泉州市鲤城区九年级(上)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年福建省泉州市惠安县九年级(上)期末数学试卷(含解析): 这是一份2022-2023学年福建省泉州市惠安县九年级(上)期末数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年福建省泉州市德化县九年级(上)期末数学试卷(含解析): 这是一份2022-2023学年福建省泉州市德化县九年级(上)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













